最短路径算法——Dijkstra,Bellman-Ford,Floyd-Warshall,Johnson
根据DSqiu的blog整理出来 :http://dsqiu.iteye.com/blog/1689163
PS:模板是自己写的,如有错误欢迎指出~
本文内容框架:
§1 Dijkstra算法
§2 Bellman-Ford算法
§3 Floyd-Warshall算法
§4 Johnson算算法
§5 问题归约
§0 小结
常用的最短路径算法有:Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法
最短路径算法可以分为单源点最短路径和全源最短路径。
单源点最短路径有Dijkstra算法和Bellman-Ford算法,其中Dijkstra算法主要解决所有边的权为非负的单源点最短路径,Bellman-Ford算法可以适用权值有负值的问题。
全源最短路径主要有Floyd-Warshall算法和Johnson算法,其中Floyd算法可以检测图中的负环并可以解决不包括负环的图中全源最短路径问题,Johnson算法相比Floyd-Warshall算法,效率更高。
算法性能分析
在分别讲解这四个算法之前先来理清下这个四个算法的复杂度:Dijkstra算法直接实现时间复杂度是O(n²),空间复杂度是O(n)(保存距离和路径),二叉堆实现时间复杂度变成O((V+E)logV),Fibonacci Heap可以将复杂度降到O(E+VlogV);Bellman-Ford算法时间复杂度是O(V*E),SPFA是时间复杂度是O(kE);Floyd-Warshall算法时间复杂度是O(n³),空间复杂度是O(n²);Johnson算法时间复杂度是O( V * E * lgd(V) ),比Floyd-Warshall算法效率高。
最短路径算法之Dijkstra算法
§1 Dijkstra算法
Dijkstra算法思想
Dijkstra算法思想为:设G=(V,E)是一个带权有向图(无向可以转化为双向有向),把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将 加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
Dijkstra算法具体步骤
(1)初始时,S只包含源点,即S={v},v的距离dist[v]为0。U包含除v外的其他顶点,U中顶点u距离dis[u]为边上的权值(若v与u有边) )或∞(若u不是v的出边邻接点即没有边<v,u>)。
(2)从U中选取一个距离v(dist[k])最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u(u∈ U)的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权(即如果dist[k]+w[k,u]<dist[u],那么把dist[u]更新成更短的距离dist[k]+w[k,u])。
(4)重复步骤(2)和(3)直到所有顶点都包含在S中(要循环n-1次)。
Dijkstra算法的邻接表实现:
Cpp代码
1 /* Dijkstra >> 优先队列优化 */ 2 typedef pair<int,int> pii; 3 struct node{ 4 int first; 5 }nod[MAXN]; 6 struct edge{ 7 int next,to,v; 8 }e[MAXM]; 9 bool vis[MAXN]; 10 int dis[MAXN]; 11 void dijkstra (int st){ 12 memset(vis,0,sizeof vis); 13 for(int i=0;i<n;i++)dis[i]=INF; 14 dis[st]=0; 15 priority_queue < pii,vector<pii>,greater<pii> > q; //pair used to save(d[i],i) 16 q.push(make_pair(0,st)); 17 while(!q.empty()){ 18 pii x=q.top();q.pop(); 19 int u=x.second; 20 if(vis[u])continue; 21 vis[u]=1; 22 for(int i=nod[u].first;i!=-1;i=e[i].next)if(dis[e[i].to]>dis[u]+e[i].v){ 23 dis[e[i].to]=dis[u]+e[i].v; 24 q.push(make_pair(dis[e[i].to],e[i].to)); 25 } 26 } 27 }
最短路径算法之Bellman-Ford算法
§2 Bellman-Ford算法
Bellman-Ford算法思想
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
Bellman-Ford算法流程:
(1) 初始化:将除源点外的所有顶点的最短距离估计值 d[v] ←+∞, d[s] ←0;
(2) 迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
(3) 检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
算法描述如下:
Bellman-Ford(G,w,s) :boolean //图G ,边集 函数 w ,s为源点
1 for each vertex v ∈ V(G) do //初始化 1阶段
2 d[v] ←+∞
3 d[s] ←0; //1阶段结束
4 for i=1 to |v|-1 do //2阶段开始,双重循环。
5 for each edge(u,v) ∈E(G) do //边集数组要用到,穷举每条边。
6 If d[v]> d[u]+ w(u,v) then //松弛判断
7 d[v]=d[u]+w(u,v) //松弛操作 2阶段结束
8 for each edge(u,v) ∈E(G) do
9 If d[v]> d[u]+ w(u,v) then
10 Exit false
11 Exit true
下面给出描述性证明:
首先指出,图的任意一条最短路径既不能包含负权回路,也不会包含正权回路,因此它最多包含|v|-1条边。
其次,从源点s可达的所有顶点如果 存在最短路径,则这些最短路径构成一个以s为根的最短路径树。Bellman-Ford算法的迭代松弛操作,实际上就是按顶点距离s的层次,逐层生成这棵最短路径树的过程。
在对每条边进行1遍松弛的时候,生成了从s出发,层次至多为1的那些树枝。也就是说,找到了与s至多有1条边相联的那些顶点的最短路径;对每条边进行第2遍松弛的时候,生成了第2层次的树枝,就是说找到了经过2条边相连的那些顶点的最短路径……。因为最短路径最多只包含|v|-1 条边,所以,只需要循环|v|-1 次。
每实施一次松弛操作,最短路径树上就会有一层顶点达到其最短距离,此后这层顶点的最短距离值就会一直保持不变,不再受后续松弛操作的影响。(但是,每次还要判断松弛,这里浪费了大量的时间,怎么优化?单纯的优化是否可行?)
如果没有负权回路,由于最短路径树的高度最多只能是|v|-1,所以最多经过|v|-1遍松弛操作后,所有从s可达的顶点必将求出最短距离。如果 d[v]仍保持 +∞,则表明从s到v不可达。
如果有负权回路,那么第 |v|-1 遍松弛操作仍然会成功,这时,负权回路上的顶点不会收敛。
1.Bellman-Ford算法实现:
Cpp代码
1 /* Bellman-Ford (若有负权环路则返回false) */ 2 struct node{ 3 int first; 4 }nod[MAXN]; 5 struct edge{ 6 int next,to,v; 7 }e[MAXM]; 8 bool inq[MAXN]; //used to note whether u node is in queue. 9 int dis[MAXN]; 10 int Bellman_Ford (int st){ 11 memset(inq,0,sizeof inq); 12 for(int i=0;i<n;i++)dis[i]=INF; 13 dis[st]=0; 14 inq[st]=true; 15 for(int i=0;i<n;i++){ 16 for(int u=0;u<n;u++)if(inq[u]){ 17 inq[u]=false; 18 for(int ed=nod[u].first;ed!=-1;ed=e[ed].next)if(dis[e[ed].to]>dis[u]+e[ed].v){ 19 dis[e[ed].to]=dis[u]+e[ed].v; 20 inq[e[ed].to]=true; 21 } 22 } 23 } 24 for(int i=0;i<n;i++)if(inq[i])return false; 25 return true; 26 }
2.SPFA——Bellman-Ford算法优化
有队列替代循环过程,对无负权环路的图更快。
Cpp代码
1 /* SPFA (无负权环路) */ 2 struct node{ 3 int first; 4 }nod[MAXN]; 5 struct edge{ 6 int next,to,v; 7 }e[MAXM]; 8 int dis[MAXN]; 9 void spfa (int st){ 10 queue <int> q; 11 for(int i=0;i<n;i++)dis[i]=INF; 12 dis[st]=0; 13 q.push(st); 14 while(!q.empty()){ 15 int u=q.top();q.pop(); 16 int i=nod[u].first; 17 for(;i!=-1;i=e[i].next)if(dis[e[i].to]>dis[u]+e[i].v){ 18 dis[e[i].to]=dis[u]+e[i].v; 19 q.push(e[i].to); 20 } 21 } 22 }
最短路径算法之Floyd-Warshall算法
§3 Floyd-Warshall算法
Floyd-Warshall算法是解决任意两点间的最短路径的算法,可以处理有向图或负权值的最短路径问题,同时也被用于计算有向图的传递闭包。算法的时间复杂度为O(n³),空间复杂度为O(n²)。
Floyd-Warshall算法的原理是动态规划。
设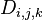 为从
为从 到
到 的只以
的只以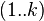 集合中的节点为中间節点的最短路径的长度。
集合中的节点为中间節点的最短路径的长度。
- 若最短路径经过点k,则
![D_{i,j,k}=D_{i,k,k-1}+D_{k,j,k-1}]() ;
; - 若最短路径不经过点k,则
![D_{i,j,k}=D_{i,j,k-1}]() 。
。
因此,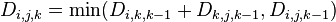 。
。
在实际算法中,为了节约空间,可以直接在原来空间上进行迭代,这样空间可降至二维。
Floyd-Warshall算法实现
Cpp代码
1 /* Floyd part */ 2 for(int k =1 ; k <= n ; k ++ ){ 3 for(int i =1 ; i<= n ; i++){ 4 for(int j =1 ;j<=n;j++){ 5 dis[ i ][ j ]= min( dis[ i ][ j ],dis[ i ][ k ]+dist[ k ][ j ] ); 6 } 7 } 8 } 9 /* 如果dis[i][j]不存在用INF代替 */
最短路径算法之Johnson算法
§4 Johnson算算法
Johson算法是目前最高效的在无负环可带负权重的网络中求所有点对最短路径的算法. Johson算法是Bellman-Ford算法, Reweighting(重赋权重)和Dijkstra算法的大综合. 对每个顶点运用Dijkstra算法的时间开销决定了Johnson算法的时间开销. 每次Dijkstra算法(d堆PFS实现)的时间开销是O( E * lgd(V) ). 其中E为边数, V为顶点数, d为采用d路堆实现优先队列ADT. 所以, 此种情况下Johnson算法的时间复杂度是O( V * E * lgd(V) )。
Johnson算法具体步骤(翻译自wikipedia):
1.初始化,把一个node q添加到图G中,使node q 到图G每一个点的权值为0。
2.使用Bellman-Ford算法,从源点为q,寻找每一个点 v从q到v的最短路径h(v),如果存在负环的话,算法终止。
3.使用第2步骤中Bellman-Ford计算的最短路径值对原来的图进行reweight操作(重赋值):边<u,v>的权值w(u,v),修改成w(u,v)+h(u)-h(v)。
4.最后,移去q,针对新图(重赋值之后的图)使用Dijkstra算法计算从每一个点s到其余另外点的最短距离。
Johnson算法实现:
Cpp代码
1 /* Johnson O(V*E*logdV */ 2 struct node{ 3 int first; 4 }nod[MAXN]; 5 struct edge{ 6 int next,to,from,v; 7 }e[MAXM]; 8 int sz; //number of edges. 9 bool inq[MAXN]; //used to note whether u node is in queue. 10 int dis[MAXN],d[MAXN][MAXN]; 11 int johnson (){ 12 memset(inq,0,sizeof inq); 13 for(int i=1;i<=n;i++)dis[i]=INF; 14 dis[0]=0; 15 for(int i=1;i<=n;i++){ 16 e[sz].next=nod[0].first; 17 e[sz].from=0;e[sz].to=i;e[sz].v=0; 18 nod[0].first=sz++; 19 } 20 inq[0]=true; 21 for(int i=1;i<=n;i++){ 22 for(int u=1;u<=n;u++)if(inq[u]){ 23 inq[u]=false; 24 for(int ed=nod[u].first;ed!=-1;ed=e[ed].next)if(dis[e[ed].to]>dis[u]+e[ed].v){ 25 dis[e[ed].to]=dis[u]+e[ed].v; 26 inq[e[ed].to]=true; 27 } 28 } 29 } 30 for(int i=0;i<n;i++)if(inq[i])return false; 31 for(int i=0;i<sz;i++)e[i].v=e[i].v-dis[to]+dis[from]; 32 /*then run the dijkstra from every node.*/ 33 for(int i=1;i<=n;i++)dijkstra(i); 34 return true; 35 }
§5 问题归约
对于两个问题A和B,如果使用求解B的一个算法来开发一个求解A的算法,且最坏的情况下算法总时间不会超过最坏情况下求解B的算法运行时间的常量倍,则称问题A可归约(reduce)为问题B。
1.传递闭包问题可归约为有非负权值的所有对最短路径问题。
给定两点u和v,有向图中从u到v存在一条路径,当且仅当网中从u到v的路径长度非零。
2.在边权没有限制的网中,(单源点或所有对)最长路径和最短路径问题是等价的。
3.作业调度问题可归约为差分约束问题。
4.有正常数的差分约束问题等价于无环网中的单源点最长路径。
5.带有截止期的作业调度问题可归约为(允许带有负权值的)最短路径问题。
§6 最短路径的扩展与应用
1.k短路
i.e:求从起点s到终点t的第k短的路,即k短路问题。
先用dijkstra从t反向寻找最短路。然后使用A*算法,把f(i)=g(i) + h(i)。h(i)就是i点到t的最短距离。当某点出队次数达到k次的时候,结果为该点的当前路程+该点到t的最短距离。(我没有判断不连通的情况)
2.差分约束系统
i.e:给出一系列类似 xi-xj<=bij 的不等式,成为差分约束系统。
为了解决这个问题,可以将不等式变形,如 xi<=xj+bij,然后转化为最短路问题。
设置一个源点,xi 看做 i 点到源点的最短路,则 bij 是路径 i 到 j 的权值,一开始设置各点到源点的距离为一个常数C,(C其实可以任意,因为对于一个解系x,x+C一定构成另一个解系。)
对于构造好的无向图,可以用Dijkstra或SPFA解决 O(∩_∩)O
3.DAG图上的单源点最短路径
只用把无向图的Dijkstra改成有向图就可以。
4.Flyod求最小环
最小环:所有环中带权长度最小的(只允许绕一圈)。
可以进行m次Dijkstra,每次删一条边w(i,j),求dis(j,i)最短路,再更新最小环,时间复杂度O(E*E*logdV)。
也可以再Floyd过程中求出,时间复杂度O(n^3)。当k进行到L-1时,已经求得所有以0,1,……,L-1为中间节点的最短路径,
设cir(L)为环上最大节点编号为L的环中的最小长度。
则cir(L)=min{w(i,L)+w(L,j)+dis(j,i)|i-->L & L-->j存在} (dis(i,j)为当前i到j的最短路)
整个Floyd走完,取cir(0,1,……,n-1)的最小值。
基本就是完整版了,里面有很多按自己的理解写的,代码有些还没有经过题目检验,如有错误恳请斧正~


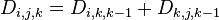 ;
;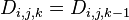 。
。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号