二叉树的封装

一. 源代码 BiTree.h

  1 #include<iostream>
  2 typedef char TElemType;  // 方便移植，方便控制树节点元素的数据类型
  3 typedef TElemType   Tree_Data;//提高程序可读性
  4 typedef  struct  BiTNode{    //定义存储结构，
  5     Tree_Data  data;
  6     struct BiTNode  *lchild,*rchild;
  7 }BiTNode, *Tree;     //树的存储结构，在类的内部嵌套 
  8 typedef Tree SElemType;//确定栈的数据元素
  9 typedef Tree  QElemType;
 10 #include "F:\A_Programer\DataStructure\Class\Stack.h"//包含栈的操作
 11 #include "F:\A_Programer\DataStructure\Class\Queue_1.h"//包含队列操作
 12 #include "F:\A_Programer\DataStructure\Class\Queue.h"//包含队列操作
 13 using namespace std;
 14 class BiTree
 15 {
 16 private:
 17     Tree T;
 18     Tree T1;
 19 public:
 20     BiTree();//初始化一棵树
 21     void CreateBiTree_BF();//以广度优先建立一棵树
 22     bool ClearBiTree();//主动销毁一棵树
 23     void PreOrderTraverse(Tree t);//前序遍历
 24     void InOrderTraverse(Tree t);//中序遍历
 25     void PostOrderTraverse(Tree t);//后序遍历
 26     void PreOrderTraverse_Thr(Tree t);//前序遍历,线性
 27     void InOrderTraverse_Thr(Tree t);//中序遍历，线性
 28     void PostOrderTraverse_Thr(Tree t);//后序遍历，线性
 29     void LevelOrderTraverse();//广度优先遍历 BFS    层序遍历
 30     void LevelOrderTraverseT1();
 31     Tree GetTree();
 32     Tree GetTree1();
 33     ~BiTree();//被动销毁一棵树
 34 };
 35 BiTree::BiTree()
 36     {
 37         T=(Tree)new BiTNode;  //申请一个树节点，并强制类型转换，作为树的头结点
 38         T->lchild=NULL;//左子树置空
 39         T->rchild=NULL;//右子树置空
 40     }
 41 void BiTree::LevelOrderTraverse()
 42 {   
 43     /*
 44         思路：（参考书目ISB 978-7-118-05852）
 45         1. 访问元素所指结点
 46         2. 若该元素所指结点左右子树不空时，则将左右子树依次入队
 47         3. 不断循环，直到队列为空
 48     */
 49     Queue Q;//初始化队列,这个队列用来存放树的节点；
 50     Queue1 Q1;//初始化队列，这个队列用来存放节点编号，方便建立树；
 51     int lab=1;//第一个节点编号
 52     Q.EnterQueue(T);//将树根放入队列
 53     Q1.EnterQueue(lab);//赋予其编号
 54     while(!Q.IsEmpty())//结束条件
 55     {   
 56         Tree t;//临时变量，树节点
 57         int num;//临时变量，节点编号
 58         Q1.DeleteQueue(&num);//出队操作
 59         Q.DeleteQueue(&t);//出队操作
 60         cout<<num<<"节点的值"<<t->data<<endl;//输出节点的值
 61         if(t->lchild!=NULL)//队列先进先出，左子树先入队
 62         {
 63             Q.EnterQueue(t->lchild);//入队操作
 64             num=Q1.GetRear();//获取队位元素的值
 65             num++;//++便是此节点的编号
 66             Q1.EnterQueue(num);//入队
 67         }
 68         if(t->rchild!=NULL)//队列先进先出，右子树后入队
 69         {
 70             Q.EnterQueue(t->rchild);//入队操作
 71             num=Q1.GetRear();//获取队位元素的值
 72             num++;//++便是此节点的编号
 73             Q1.EnterQueue(num);//入队
 74         }
 75     }
 76 }
 77 void BiTree::CreateBiTree_BF()
 78 {   
 79     /*
 80         关键注意
 81         1.  左子树先入队，右子树后入队
 82         2.  注意入队与出队时机
 83      */
 84     Queue Q;//初始化队列,这个队列用来存放树的节点
 85     Queue1 Q1;//初始化队列，这个队列用来存放节点编号，方便建立树
 86     int num=1;//第一个节点编号
 87     Q.EnterQueue(T);//将树根放入队列
 88     Q1.EnterQueue(num);//赋予其编号
 89     bool b;//用来判断是否具有左或右子树，由用户输入
 90     Tree t;//临时变量
 91     while(!Q.IsEmpty())//结束条件
 92     {   
 93         Q1.DeleteQueue(&num);//出对操作
 94         cout<<"请输入"<<num<<"节点的值"<<endl;//提示信息
 95         Q.DeleteQueue(&t);//出对操作
 96         cin>>t->data;//赋值
 97         cout<<"此节点是否具有左子树"<<endl;//提示信息
 98         cout<<"是           1"<<endl;
 99         cout<<"否           0"<<endl;
100         cin>>b;//输入布尔量
101         if(b)//如果有左子树，则先将其入队
102         {
103             Tree p=new BiTNode;//新建节点
104             t->lchild=p;//赋值
105             Q.EnterQueue(p);//入队
106             num=Q1.GetRear();//获取队尾元素
107             num++;//++便是该节点编号
108             Q1.EnterQueue(num);//入队
109         }
110         else
111             t->lchild=NULL;//赋值为空
112         cout<<"是否具有右子树"<<endl;//提示信息
113         cout<<"是           1"<<endl;
114         cout<<"否           0"<<endl;
115         cin>>b;//输入布尔量
116         if(b)//如果有有子树，则后将其入队
117         {
118             Tree p=new BiTNode;//新建节点
119             t->rchild=p;//赋值
120             Q.EnterQueue(p);//入队
121             num=Q1.GetRear();//获取队尾元素
122             num++;//++便是该节点编号
123             Q1.EnterQueue(num);//入队
124         }
125         else t->rchild=NULL;//赋值为空
126     }
127 }
128 void BiTree::PreOrderTraverse( Tree t)
129 {   
130     if(t)//结束条件
131     {
132         cout<<t->data<<endl;          //输出根节点的值
133         PreOrderTraverse(t->lchild);  //访问左子树
134         PreOrderTraverse(t->rchild);  //访问右子树
135     }
136 }
137 Tree BiTree::GetTree()
138 {
139     return this->T;
140 }
141 Tree BiTree::GetTree1()
142 {
143     return this->T1;
144 }
145 void BiTree::InOrderTraverse(Tree t)
146 {
147     if(t)//递归结束条件
148     {
149         InOrderTraverse(t->lchild);//首次寻找空树的左节点
150         cout<<t->data<<endl;   //首次作为根访问   
151         InOrderTraverse(t->rchild);//首次访问为空树的右节点
152         //结束时以t为根节点的树已访问完毕
153     }
154 }
155 void BiTree::PostOrderTraverse(Tree t)
156 {
157     if(t)
158     {
159         PostOrderTraverse( t->lchild);  //   首次访问的树必定为一颗空树，代表此节点访问结束，在此基础上逐步递归，访问其他节点； 不管哪种递归方式，访问他的时候必定作为根，相对于空树
160         PostOrderTraverse( t->rchild);
161         cout<<t->data<<endl;
162     }
163 }
164 void BiTree::PreOrderTraverse_Thr(Tree t)
165 {   
166     /*
167         先序遍历
168         非递归实现方法
169         思路如下：
170         访问思路
171         1. 不断访问根节点，并且压入栈，直到寻找第一课空树，，且这个空树树必定作为其所在树的左子树；
172         2. 访问栈顶节点，如果栈顶节点的右孩子为空，则此节点已经失去价值，弹出； 否者，将其作为一颗新树访问，重复上述过程；
173         3. 循结束环条件，栈空；
174         我们应当重点考察的位置是 ***入栈时机与出栈时机***                           
175     */
176     Stack S;// 初始化栈
177     S.Push(t);//将根节点入栈
178     S.GetTop(&t);//获取栈顶元素
179     while(!S.IsEmpty())//结束条件
180     {
181         while(t)//t==0,结束循环,即遇到左子树为空时停止循环
182         {   
183             cout<<t->data<<endl;//访问结点
184             S.Push(t->lchild);//将左节点入栈
185             S.GetTop(&t);//更新t
186         }
187         S.Pop(&t);//最后一次入栈的是一个空指针，出栈，当然这个语句还有其他巧妙的作用
188         if(!S.IsEmpty())//栈不空，就出栈
189         {
190             S.Pop(&t);//出栈
191             S.Push(t->rchild);//将其右孩子入栈，如果这值为NULL,S.Pop(&t);"    //最后一次入栈的是一个空指针，出栈，当然这个语句还有其他巧妙的作用 "  ,这就是巧妙之处
192             S.GetTop(&t);//更新t
193         }
194         //S.Display();
195     }
196 }
197 void BiTree::InOrderTraverse_Thr(Tree t)
198 {   
199     /*
200        思路：
201          1.不断沿左子树深入，并且入栈；  直到遇到空左子树为止；
202          2.访问此节点；  
203          3.接着将此节点右子树入栈，并且将此节点出栈
204          4.重复上述过程，直到栈空
205     */
206     Stack S;//初始化话栈
207     S.Push(t);//根节点入栈
208     while(!S.IsEmpty())//栈空为结束条件
209     {
210         S.GetTop(&t);//获取栈首元素
211         while(t)//不断深入左子树，直到左子树为空树
212         {
213             t=t->lchild;//更新t
214             S.Push(t);//将左子树入栈
215         }
216         S.Pop(&t);//最后一次入栈的是一个空指针，出栈，当然这个语句还有其他巧妙的作用
217         if(!S.IsEmpty())//栈不空，就出栈
218         {
219             S.Pop(&t);//出栈
220             cout<<t->data<<endl;//访问该节点
221             S.Push(t->rchild);//将其右孩子入栈，如果这值为NULL,“S.Pop(&t);    //最后一次入栈的是一个空指针，出栈，当然这个语句还有其他巧妙的作用 "  ,这就是巧妙之处
222         }
223     }
224 }
225 void BiTree::PostOrderTraverse_Thr(Tree t)
226 {   
227     /* 
228        关键技术：
229           采用节点保留技术，来判断是否访问当前节点
230           在这个程序中采用pre来保留节点
231           pre==NULL 这是其初值
232           在此之后其的值都将为先前前访问过的节点
233        思路：
234           1.对于首个节点，现将自己入栈（根）
235           2.处理栈顶元素
236              （1）访问该节点的条件
237                  【1】 当前节点的左右子树都为空；（t->lchild==NULL&&t->rchild==NULL） ，这个条件将用来第一次更新pre的值
238                  【2】 pre!=NULL&&(t->rchild==pre||t->lchild==pre)
239                        解释
240                        *1 其中pre！=NULL ，主要作用起在第一次深入过程中，只有这样才能将所有元素入栈
241                        *2 在第一次pre被更新后，这语句的作用更新为（或者说等同于，因为pre不可能再为NULL）t->rchild==pre||t->lchild==pre
242                           第一层：  t->rchild==pre   
243                                                 在t的右子树且左子树存在的情况下，此语句起作用
244                                                 在t的右子树且左子树不存在的情况下，此语句也起作用（因为这俩种情况最先弹出的元素必定为节点的右子树）
245                           第二层： t->lchild==pre
246                                                当且仅当t只有左子树是时，语句起作用
247                           
248              （2）将右子树入栈（当然如果是空树就不入栈）！！！！ 很重要，后将左子树入栈 （当然如果是空树就不入栈）
249           
250     */
251     Tree pre=NULL;  //初始化为空值
252     Stack S;   //初始化栈
253     S.Push(t); //将根节点入栈
254     while(!S.IsEmpty())
255     {   
256         S.GetTop(&t);//更新t,处理栈首元素
257         if((t->lchild==NULL&&t->rchild==NULL)||(pre!=NULL&&(t->rchild==pre||t->lchild==pre)))//出栈的情况，即是否可访问该节点的条件，否则继续深入
258         {
259             cout<<t->data<<endl;//访问该节点
260             S.Pop(&t);//该节点失去存在的意义，出栈
261             pre=t;//更新pre
262         }
263         else//继续入栈的情况
264         {
265             if(t->rchild!=NULL)//先将右子树入栈，空树不如栈
266             {
267                 S.Push(t->rchild);
268             }
269             if(t->lchild!=NULL)//再将右子树入栈，空树不如栈，这个很关键
270             {
271                 S.Push(t->lchild);
272             }
273         }
274     }
275 }
276 BiTree::~BiTree()
277 {
278     /*
279         宽度优先删除节点
280     */
281     Tree t;//临时变量
282     t=T;//将根节点赋值
283     Queue Q;//初始化队列
284     Q.EnterQueue(t);//入队
285     while(!Q.IsEmpty())//结束条件
286     {
287         Q.DeleteQueue(&t);//处理队首元素
288         if(t->lchild!=NULL)//榨取节点利用价值
289         {
290             Q.EnterQueue(t->lchild);//保存有效信息
291         }
292         if(t->rchild!=NULL)//榨取节点利用价值
293         {
294             Q.EnterQueue(t->rchild);//保存有效信息
295         }
296         free(t);//抛弃无用节点
297     }
298 }

几点说明

1.#include "F:\A_Programer\DataStructure\Class\Stack.h"//包含栈的操作可参考我的其他随笔，有详细解释

　　代码如下：

#pragma once
#include<iostream>
#include<cstring>
typedef  SElemType  Stack_Data;  //栈的数据类型
const int  Stack_Size=50;   //栈的最大存储量
using namespace std;
class Stack               
{  
private:
     Stack_Data Data[Stack_Size];
     int Top;
public:
    Stack(); //初始化栈
    bool IsEmpty();//判空
    bool IsFull();//判满
    void Push(Stack_Data e);// 入栈
    bool Pop(Stack_Data *e);//出栈
    void GetTop(Stack_Data *e);//取栈顶元素
    void Display();//展示函数
    int  TopLocation();//获取Top
};
Stack::Stack()
{
    Top=0;
}
bool Stack:: IsEmpty()
{
    if(Top==0)
    {
        return true;
    }
    else 
        return false;
}
bool Stack::IsFull()
{
    if(Top==Stack_Size-1)
    {
        return true;
    }
    else 
        return false;
}
void Stack::Push(Stack_Data e)
{
    if(!IsFull())
    {
        Top++;
        Data[Top]=e;
    }
    else
        cout<<"Stack OverFlow"<<endl;
}   
bool Stack::Pop(Stack_Data *e)
{
    if(!IsEmpty())
    {
        *e=Data[Top];
        Top--;
        return true;
    }
    else
        cout<<"Defeat"<<endl;
        return false; 
}
void Stack::GetTop(Stack_Data *e)
{
     if(!IsEmpty())
     {
         *e=Data[Top];
     }
     else 
         cout<<"Defeat"<<endl;
}
void Stack::Display()
{   
    if(!IsEmpty())
    {
        int temp=Top;
        while(temp)
        {
            cout<<"Data["<<temp<<"]   "<<Data[temp]->data<<endl;
            temp--;
        }
    }
    else
        cout<<"False"<<endl;
}
int  Stack::TopLocation()
{
    return Top;
}

2. #include "F:\A_Programer\DataStructure\Class\Queue.h"//包含队列操作可参考我的其他随笔，有详细解释

 1 #pragma once
 2 #include<iostream>
 3 using namespace std;
 4 #define QMaxSize 100  //队列最大容量
 5 typedef QElemType   Queue_Data;   //队列存储元素类型
 6 typedef struct QueueNode               //存储结构
 7 {
 8     Queue_Data data[QMaxSize];
 9     int front;
10     int rear;
11     int count;
12 }QueueNode,*Que;
13 class  Queue
14 {
15 private:
16     Que  Q;
17 public:
18     Queue();//初始化空的队列
19     bool EnterQueue(Queue_Data e);// 入队操作
20     bool DeleteQueue(Queue_Data *e);//出队操作；
21     bool IsEmpty();//判空
22     bool IsFull();//判满
23     void Display();
24 };
25 Queue::Queue()
26     {  
27         Q=new QueueNode;
28         Q->front=0;
29         Q->rear=0;
30         Q->count=0;
31     }
32 bool Queue::EnterQueue(Queue_Data e)
33 {
34     if(!IsFull())//如果队列不满的话，增加元素
35     {
36         Q->count++;//计数器示数即为队列元素个数
37         Q->data[Q->rear]=e;//队尾指针所指空间即为下一个入队元素的存放位置
38         Q->rear=(Q->rear+1)%QMaxSize;//队列的精华
39         return true;
40     }
41     else return false;
42 }
43 bool Queue::DeleteQueue(Queue_Data *e)
44 {
45     if(!IsEmpty())//如果队列不为空，操作合法
46     {
47         *e=Q->data[Q->front];//队首指针指示位置即为要出队元素的位置
48         Q->front=(Q->front+1)%QMaxSize;//这里容易出错，切记是加一
49         Q->count--;
50         return true;
51     }
52     else return false;
53 }
54 bool Queue::IsEmpty()
55 {
56     if(Q->count==0)//判空最简单的一种计数器方法
57         return true;
58     else 
59         return false;
60 }
61 bool Queue::IsFull()
62 {
63     if(Q->count==QMaxSize)//判满，计数器
64         return true;
65     else 
66         return false;
67 }
68 void Queue::Display()
69 {  
70     int b;
71     int p;
72     b=Q->count;
73     p=Q->front;
74     while(b)
75     {
76         cout<<Q->data[p]<<endl;
77         p=(p+1)%QMaxSize;
78         b--;
79     }
80 }

3.#include "F:\A_Programer\DataStructure\Class\Queue_1.h"//包含队列操作

#include<iostream>
using namespace std;
#define QMaxSize_1 100  //队列最大容量
typedef int  QElemType_1;
typedef QElemType_1   Queue_Data_1;  //队列存储元素类型
typedef struct QueueNode1                //存储结构
{
    Queue_Data_1 data[QMaxSize_1];
    int front;
    int rear;
    int count;
}QueueNode_1,*Que_1;
class  Queue1
{
private:
    Que_1  Q;
public:
    Queue1();//初始化空的队列
    bool EnterQueue(Queue_Data_1 e);// 入队操作
    bool DeleteQueue(Queue_Data_1 *e);//出队操作；
    bool IsEmpty();//判空
    bool IsFull();//判满
    Queue_Data_1 GetRear();
    void Display();
};
Queue1::Queue1()
    {  
        Q=new QueueNode1;
        Q->front=0;
        Q->rear=0;
        Q->count=0;
    }
bool Queue1::EnterQueue(Queue_Data_1 e)
{
    if(!IsFull())//如果队列不满的话，增加元素
    {
        Q->count++;//计数器示数即为队列元素个数
        Q->data[Q->rear]=e;//队尾指针所指空间即为下一个入队元素的存放位置
        Q->rear=(Q->rear+1)%QMaxSize_1;//队列的精华
        return true;
    }
    else return false;
}
bool Queue1::DeleteQueue(Queue_Data_1 *e)
{
    if(!IsEmpty())//如果队列不为空，操作合法
    {
        *e=Q->data[Q->front];//队首指针指示位置即为要出队元素的位置
        Q->front=(Q->front+1)%QMaxSize_1;//这里容易出错，切记是加一
        Q->count--;
        return true;
    }
    else return false;
}
bool Queue1::IsEmpty()
{
    if(Q->count==0)//判空最简单的一种计数器方法
        return true;
    else 
        return false;
}
bool Queue1::IsFull()
{
    if(Q->count==QMaxSize_1)//判满，计数器
        return true;
    else 
        return false;
}
void Queue1::Display()
{  
    int b;
    int p;
    b=Q->count;
    p=Q->front;
    while(b)
    {
        cout<<Q->data[p]<<endl;
        p=(p+1)%QMaxSize_1;
        b--;
    }
}
Queue_Data_1  Queue1::GetRear()
{
    return  this->Q->data[this->Q->rear-1];
}

二.测试代码及输入文件

1. 测试代码（主函数）

int main()
{   
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    BiTree  T;
    T.CreateBiTree_BF();
    T.LevelOrderTraverse();
    T.PreOrderTraverse(T.GetTree());
    cout<<endl;
    T.InOrderTraverse(T.GetTree());
    cout<<endl;
    T.PostOrderTraverse(T.GetTree());
    cout<<endl;
    T.PreOrderTraverse_Thr(T.GetTree());
    cout<<endl;
    T.InOrderTraverse_Thr(T.GetTree());
    cout<<endl;
    T.PostOrderTraverse_Thr(T.GetTree());
    cout<<endl;
    return 0;
}

2. in.txt

1
1
1
2
1
0
3
1
1
4
0
1
5
0
0
6
0
0
7
0
0

3. 测试树的结构

测试树

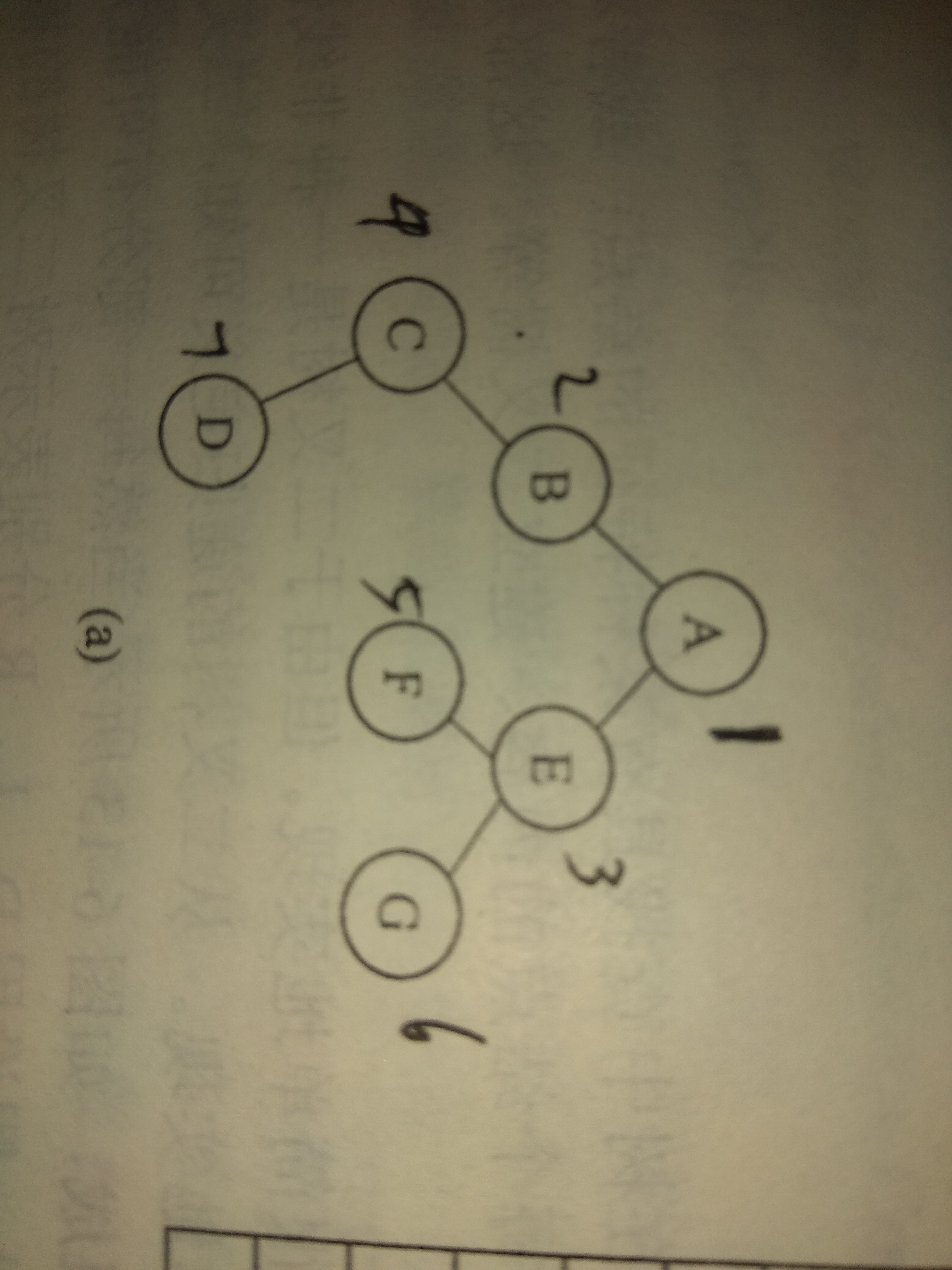
三. 测试结果

out.txt

请输入1节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入2节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入3节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入4节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入5节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入6节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
请输入7节点的值
此节点是否具有左子树
是           1
否           0
是否具有右子树
是           1
否           0
1节点的值1
2节点的值2
3节点的值3
4节点的值4
5节点的值5
6节点的值6
7节点的值7
1
2
4
7
3
5
6

4
7
2
1
5
3
6

7
4
2
5
6
3
1

posted @ 2018-04-13 16:31 Howbin 阅读(548) 评论(0) 编辑收藏举报

刷新页面返回顶部

Howbin

二叉树的封装

公告