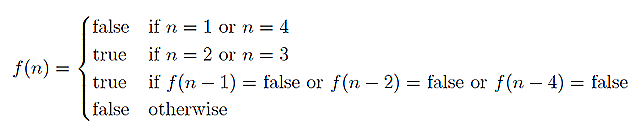一道面试题(Nim取子游戏)——如何将数学思维应用到编程中
今天偶然遇到一道Nim取子游戏的题,大意如下:
有16颗石子,两个人轮流取子,每次只能取一颗、两颗或者四颗石子,最后取完石子的人为负。问,先取子的人还是后取子的人有必胜策略。
题目非常简单,已经非常熟悉博弈论或者Nim取子游戏的大牛,请移步进阶话题。
寻找思路
拿到一个特殊化的题目,如果没有思路的话,可以考虑先将题目转换为一般化的形式,再将一般化形式的题目特殊化到简单实例寻找规律。以本题为例,先将题目转换为一般形式:
有 n 颗石子,两个人轮流取子,每次只能取一颗、两颗或者四颗石子,最后取完石子的人为负。问,先取子的人还是后取子的人有必胜策略。
考虑简单的情况:
当 n = 1 时,先取子的人必然取完全部的石子,因此,先取子的人必负,从而后取子的人必胜;即,当 n = 1 时,后取子的人有必胜策略。
当 n = 2 时,先取子的人可以只取一颗石子,从而后取子的人进入上述 n = 1 时先取子的情况;因此,当 n = 2 时,先取子的人有必胜策略。
当 n = 3 时,先取子的人可以只取两颗石子,从而后取子的人进入上述 n = 1 时先取子的情况;因此,当 n = 3 时,先取子的人有必胜策略。
当 n = 4 时,先取子的人若只取一颗石子,则后取子的人将进入上述 n = 3 时先取子的情况,后取子的人必胜;若先取子的人只取两颗石子,则后取子的人将进入上述 n = 2 时先取子的情况,后取子的人必胜;先取子的人若取四颗石子,则恰将所有石子取光,从而后取子的人必胜;综上所述,当 n = 4 时,后取子的人有必胜策略。
当 n = 5 时,先取子的人若只取一颗石子,则后取子的人将进入上述 n = 4 时先取子的情况,从而必输;因此,当 n = 5 时,先取子的人有必胜策略。
为了方便起见,我们引入两个博弈论中的概念:P状态和N状态。如果双方都按照最佳策略进行游戏,我们可以将游戏中的每个状态依据其是先手必胜还是后手必胜分类。一个先手胜状态被认为是一个N状态(因为下一个玩家即将获胜),一个后手胜状态被认为是一个P状态(因为前一个玩家即将获胜)。P状态和N状态归纳性地描述如下:
一个点v是P状态当且仅当它的所有后继都为N状态
一个点v是N状态当且仅当它的一些后继是P状态
在此我们稍微详细的解释一下P状态和N状态定义的实际意义。注意以下事实:如果当前游戏处于P状态,则先走的人必输,后走的人必胜(按照P状态的定义)。因此,无论当前处于何种状态,只要按照游戏规则进行了一步后,能够进入P状态,则当前先走的人必胜。因此,N状态可以转移到P状态,而P状态必然转移到N状态。这也就是P状态和N状态归纳性描述的实际意义。
为了不被这些繁琐的概念弄晕,我们不妨回到原来这道题目上。下面,我们使用P状态和N状态来标记这个取子游戏的先手必胜或者必负的情况。(下面一行表示游戏开始时有几个石子,0 的上面对应的 * 号表示,对于初始有 0 个石子的情况,没有定义这时是谁赢)
* P N N P N N P N N P ……
0 1 2 3 4 5 6 7 8 9 10 ……
可以发现规律:当 n mod 3 = 1 时,后手有必胜策略;其余情况,先手有必胜策略。
形式化的证明
虽然我们通过观察发现了规律,但是我们不能保证我们发现的规律会一直保持下去。对于特定的这道题而言,我们只需将上面的状态转移表一直写到 n = 16 的情况即可解题。但是我们不妨把眼光放的长远一些,考虑一般形式的解。
实际上,上面寻找思路的过程中,暗示了我们应该如何证明这一结论。下面我们采用数学归纳法证明这一结论:
当 n mod 3 = 1 时,游戏处于P状态;其余情况,游戏处于N状态。
归纳基础:
当 n = 1 时,游戏处于P状态;当 n = 2 时,游戏处于N状态;当 n = 3 时,游戏处于N状态。
归纳假设:
若 n mod 3 = 0,则:(n – 3)处于N状态,(n – 2)处于P状态,(n – 1)处于N状态,n 处于N状态;
若 n mod 3 = 1,则:(n – 3)处于P状态,(n – 2)处于N状态,(n – 1)处于N状态,n 处于P状态;
若 n mod 3 = 2,则:(n – 3)处于N状态,(n – 2)处于N状态,(n – 1)处于P状态,n 处于N状态。
归纳证明:
若 n mod 3 = 0,则由于从状态(n + 1)仅可以转换到状态 n、状态(n - 1)、状态(n - 3),而这三个状态均为N状态,因此状态(n + 1)为P状态;(n + 1 mod 3 = 1)
若 n mod 3 = 1,则由于从状态(n + 1)可以转换到状态 n,而状态 n 为P状态,因此状态(n + 1)为N状态;(n + 1 mod 3 = 2)
若 n mod 3 = 2,则由于从状态(n + 1)可以转换到状态(n - 1),而状态(n - 1)为P状态,因此状态(n + 1)为N状态。(n + 1 mod 3 = 0)
综上所述,当 n mod 3 = 1 时,游戏处于P状态;其余情况,游戏处于N状态。
有了这一结论,对于给定的石子数目 n,如果按照题目中所叙述的规则来进行游戏,我们只需要判定 n mod 3 是否等于 1,即可给出先手还是后手有必胜策略的答案。因此,对应于这一题目,我们所编写的程序也相当简单了。
递归形式
对于题目中给定的这种简单情况,确实很容易发现其规律并证明其正确性。但是有的时候,解的规律是很不显然的,或者是难以证明的。对于这种情况,我们可以考虑,从工程上解决这一问题,而不是找到数学上的“紧形式”的解。放开这一限制,我们虽然抛弃了数学上的美感,但是却能够解决更广泛的一系列问题。这里不对此进行进一步的展开讨论,而是继续就本问题进行讨论。
在寻找思路的过程中,给了我们足够的提示来解决这一问题。经过细致的归纳和整理,我们可以得到一个递归的解:
从这个递归解出发,我们可以写出一个递归函数来处理这一问题:
bool f(int n)
{
if(n == 1 || n == 4) return false;
if(n == 2 || n == 3) return true;
if( !f(n - 1) || !f(n - 2) || !f(n - 4) ) return true;
return false;
}
当然,这个解显然不是最优的。例如:在计算 f (5) 的时候,我们需要计算 f (4);而在计算 f (6) 的时候,我们仍然需要计算 f (4)。这正是动态规划算法所具有的重叠子问题性质。而上面给出的递归解,则符合了动态规划算法的最优子结构性质。
动态规划解
既然这一问题满足动态规划算法的所有性质,我们可以使用较高效的动态规划算法来解决这一问题。如何重新安排计算的顺序,从而高效、无重复的计算 f (n),这是一个较为复杂的问题。但是对于现在我们所面对的这一特定问题,其答案却不难回答。我们只需要设定好初始条件,然后由小到大顺序的计算f (n),即可无重复的得到所需要的结果。一个动态规划算法如下:
bool f(int n)
{
if(n <= 0) return false;
bool *states = (bool *)malloc(sizeof(bool) * n);
states[0] = states[3] = false;
states[1] = states[2] = true;
for(int i = 4; i < n; i++) {
states[i] = !(states[i - 1]
&& states[i - 2]
&& states[i - 4]);
/* According to De Morgan's laws */
}
return states[n - 1];
}
这个算法是很容易想到的,但是考虑到我们在求递归解的时候,只需要之前的四个数据即可,我们还可以继续优化这个算法。
bool fn(int n)
{
if(n <= 0) return false; /* We can return anything, because it has no real meaning. */
if(n == 1 || n == 4) return false;
if(n == 2 || n == 3) return true;
/* a ~ fn(i - 4)
* b ~ fn(i - 3)
* c ~ fn(i - 2)
* d ~ fn(i - 1)
* f ~ fn(i)
*/
bool a = d = false, b = c = true;
for(int i = 5; i <= n; i++) {
bool f = !(a && c && d);
a = b; b = c; c = d; d = f;
}
return d;
}
进阶话题
《编程之美》P67~87