R语言学习笔记（十三）：时间序列

#生成时间序列对象
sales<-c(18,33,41,7,34,35,24,25,24,21,25,20,22,31,40,29,25,21,22,54,31,25,26,35)
tsales<-ts(sales,start=c(2003,1),frequency = 12)
tsales

     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003 18 33 41 7 34 35 24 25 24 21 25 20
2004 22 31 40 29 25 21 22 54 31 25 26 35

plot(tsales)

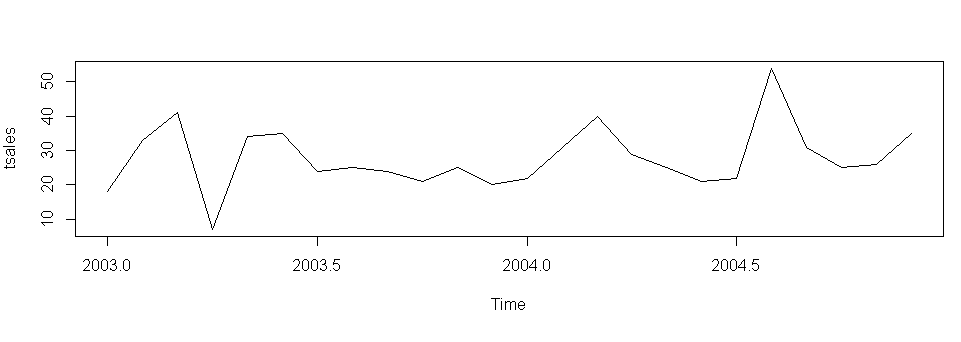
start(tsales)
[1] 2003    1


end(tsales)
[1] 2004   12


frequency(tsales)

  [1] 12

 

tsales.subset<-window(tsales,start=c(2003,5),end=c(2004,6))
tsales.subset

     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003 34 35 24 25 24 21 25 20
2004 22 31 40 29 25 21

 

 

#简单移动平均
install.packages("forecast")
library(forecast)
opar<-par(no.readonly=TRUE)
par(mfrow=c(2,2))
ylim<-c(min(Nile),max(Nile))
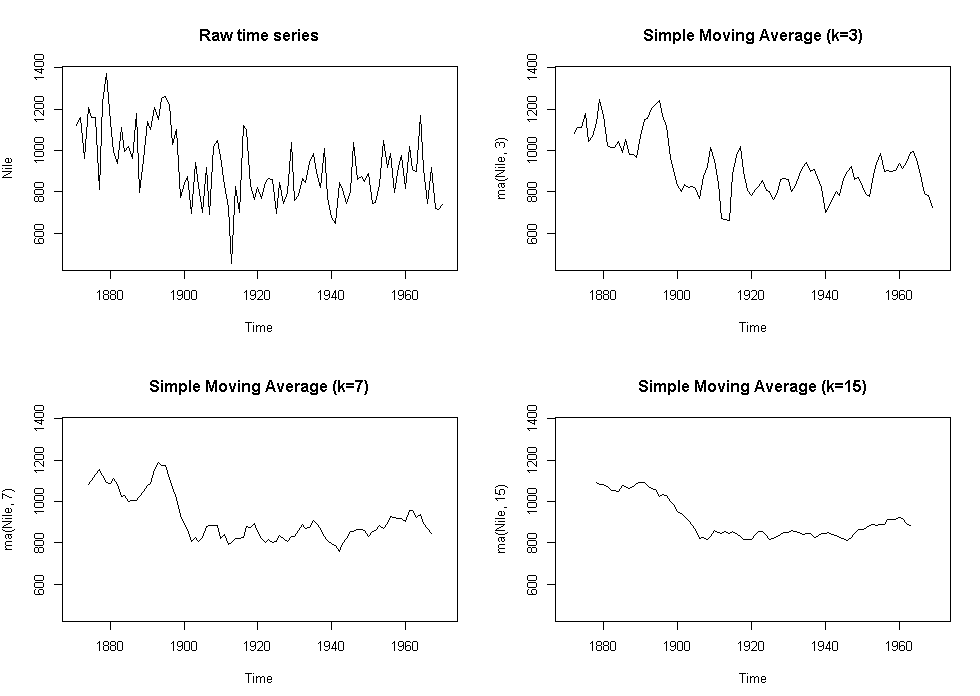
plot(Nile,main="Raw time series")
plot(ma(Nile,3),main="Simple Moving Average (k=3)",ylim=ylim)
plot(ma(Nile,7),main="Simple Moving Average (k=7)",ylim=ylim)
plot(ma(Nile,15),main="Simple Moving Average (k=15)",ylim=ylim)
par(opar)

 

#季节性分解
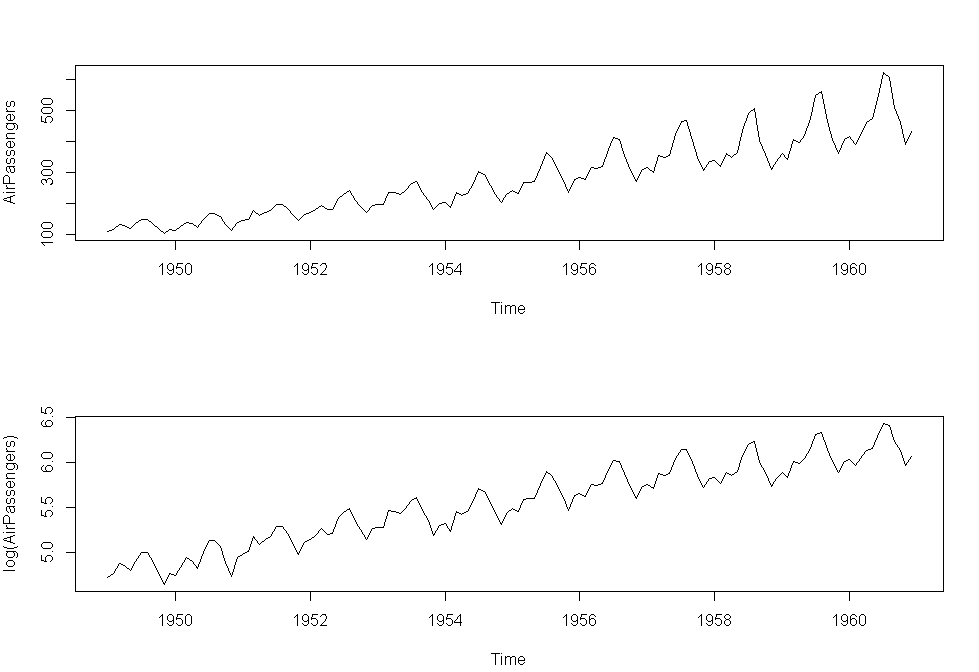
plot(AirPassengers)
lAirPassengers<-log(AirPassengers)
plot(lAirPassengers,ylab="log(AirPassengers)")

 

fit<-stl(lAirPassengers,s.window="period")
plot(fit)

 

fit$time.series
exp(fit$time.series)

par(mfrow=c(2,1))
library(forecast)
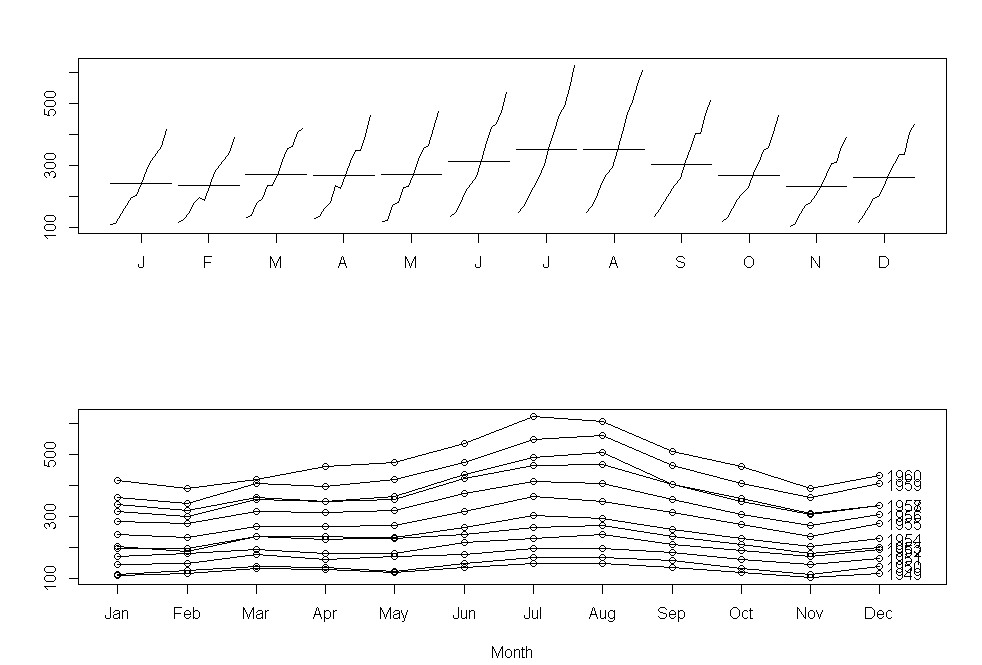
monthplot(AirPassengers,xlab="",ylab="")
seasonplot(AirPassengers,year.labels="TRUE",main="")

 

 

#单指数平滑
library(forecast)
fit<-ets(nhtemp,model="ANN")
fit

ETS(A,N,N)

Call:
ets(y = nhtemp, model = "ANN")

Smoothing parameters:
alpha = 0.182

Initial states:
l = 50.2759

sigma: 1.1263

AIC AICc BIC
265.9298 266.3584 272.2129

 

 

forecast(fit,1)

Point  Forecast Lo 80     Hi 80   Lo 95    Hi 95
1972   51.87045 50.42708 53.31382 49.66301 54.0779

 

plot(forecast(fit,1),xlab="Year",ylab=expression(paste("Temperature (",degreee*F,")",)),main="New Haven Annual Mean Temperature")

accuracy(fit)

             ME        RMSE     MAE       MPE       MAPE     MASE      ACF1
Training set 0.1460295 1.126268 0.8951331 0.2418693 1.748922 0.7512497 -0.00653111

 

ME: Mean Error

RMSE: Root Mean Squared Error

MAE: Mean Absolute Error

MPE: Mean Percentage Error

MAPE: Mean Absolute Percentage Error

MASE: Mean Absolute Scaled Error

ACF1: Autocorrelation of errors at lag 1.

 

#有水平项，斜率以及季节性的指数模型
library(forecast)
fit<-ets(log(AirPassengers),model="AAA")
fit

ETS(A,A,A)

Call:
ets(y = log(AirPassengers), model = "AAA")

Smoothing parameters:
alpha = 0.6534
beta = 1e-04
gamma = 1e-04

Initial states:
l = 4.8022
b = 0.01
s=-0.1047 -0.2186 -0.0761 0.0636 0.2083 0.217
0.1145 -0.011 -0.0111 0.0196 -0.1111 -0.0905

sigma: 0.0359

AIC AICc BIC
-208.3619 -203.5047 -157.8750

 

 

accuracy(fit)

pred<-forecast(fit,5)
pred

              ME            RMSE       MAE          MPE       MAPE      MASE      ACF1
Training set -0.0006710596 0.03592072 0.02773886 -0.01250262 0.508256 0.2291672 0.09431354

plot(pred,main="Forecast for Air Travel",ylab="Log(AirePassengers)",xlab="Time")

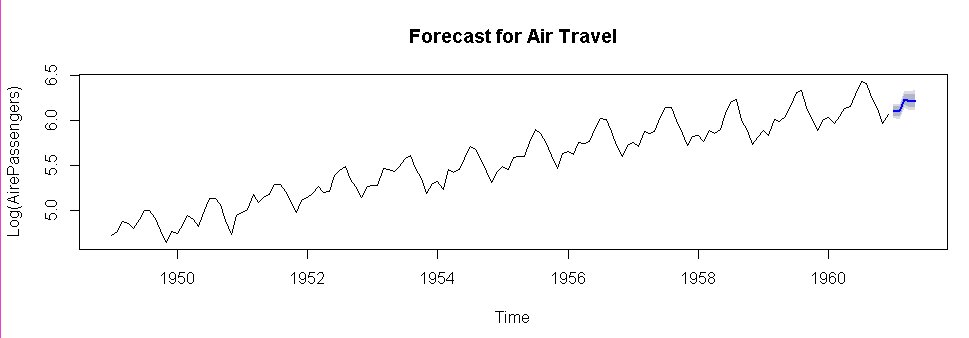
pred$mean<-exp(pred$mean)
pred$lower<-exp(pred$lower)
pred$upper<-exp(pred$upper)
p<-cbind(pred$mean,pred$lower,pred$upper)
dimnames(p)[[2]]<-c("mean","Lo 80","Lo 95","Hi 80","Hi 95")
p

          mean     Lo 80    Lo 95    Hi 80    Hi 95
Jan 1961 447.4958 427.3626 417.0741 468.5774 480.1365
Feb 1961 442.7926 419.1001 407.0756 467.8245 481.6434
Mar 1961 509.6958 478.7268 463.1019 542.6682 560.9776
Apr 1961 499.2613 465.7258 448.8949 535.2116 555.2788
May 1961 504.3514 467.5503 449.1688 544.0491 566.3135

 

 

#ETS函数的自动指数预测
library(forecast)
fit<-ets(JohnsonJohnson)
fit

ETS(M,A,M)

Call:
ets(y = JohnsonJohnson)

Smoothing parameters:
alpha = 0.1481
beta = 0.0912
gamma = 0.4908

Initial states:
l = 0.6146
b = 0.005
s=0.692 1.2644 0.9666 1.077

sigma: 0.0889

AIC AICc BIC
166.6964 169.1289 188.5738

 

plot(forecast(fit),main="Johnson & Johnson Forecasts",ylab="Quarterly Earnings (Dollars)",xlab="Time",flty=2)

 

#序列的变换以及稳定性评估
library(forecast)
library(tseries)
plot(Nile)

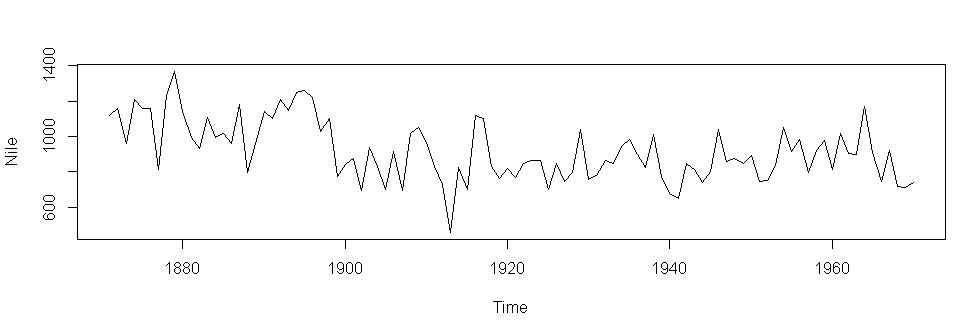
ndiffs(Nile)

[1] 1

 

dNile<-diff(Nile)
plot(dNile)

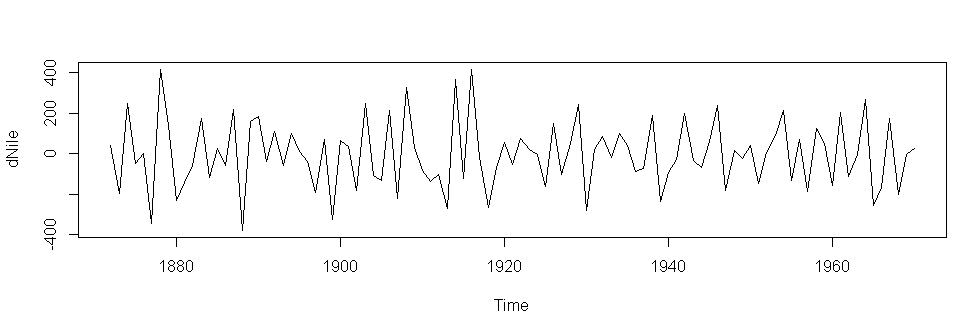
#拟合ARIMA模型
library(forecast)
fit<-arima(Nile,order=c(0,1,1))
fit

accuracy(fit)

             ME RMSE MAE MPE MAPE MASE ACF1
Training set -11.9358 142.8071 112.1752 -3.574702 12.93594 0.841824 0.1153593

 

#模型评价
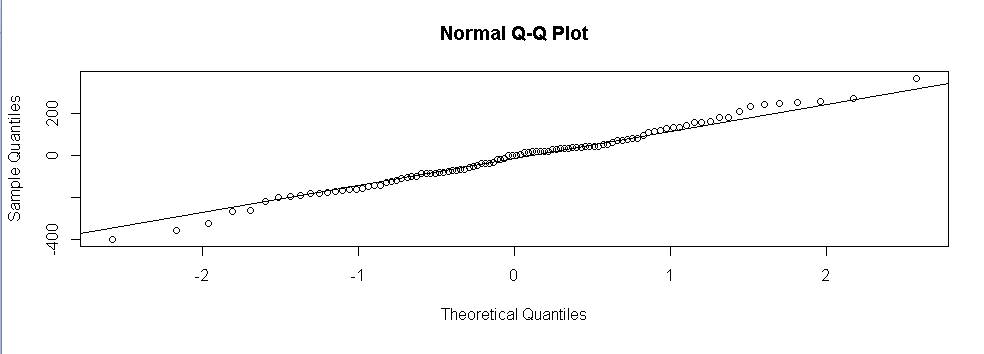
qqnorm(fit$residuals)
qqline(fit$residuals)
Box.test(fit$residuals,type="Ljung-Box")

Box-Ljung test

data: fit$residuals
X-squared = 1.3711, df = 1, p-value = 0.2416

#ARIMA 模型预测
forecast(fit,3)
plot(forecast(fit,3),xlab="Year",ylab="Annual Flow")

#ARIMA自动预测
library(forecast)
fit<-auto.arima(sunspots)
fit

Series: sunspots
ARIMA(2,1,2)

Coefficients:
ar1 ar2 ma1 ma2
1.3467 -0.3963 -1.7710 0.8103
s.e. 0.0303 0.0287 0.0205 0.0194

sigma^2 estimated as 243.8: log likelihood=-11745.5
AIC=23500.99 AICc=23501.01 BIC=23530.71

 

forecast(fit,3)

Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1984 40.43784 20.42717 60.44850 9.834167 71.04150
Feb 1984 41.35311 18.26341 64.44281 6.040458 76.66576
Mar 1984 39.79670 15.23663 64.35677 2.235319 77.35808

accuracy(fit)

ME RMSE MAE MPE MAPE MASE ACF1
Training set -0.02672716 15.60055 11.02575 NaN Inf 0.4775401 -0.01055012

 

 

小结

这章主要讲解了怎么用R语言来进行时间序列分析，例如：模型的建立，图表的绘制，以及未来趋势的预测。这类型的数据分析完全不在程序开发的范畴了，所有的分析都是基于数理统计，这应该就是现在的数据科学方向吧。