关于DFS与BFS

DFS（深度优先搜索）

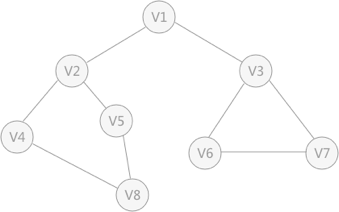
                                         为无向图

DFS的过程类似于树的先序遍历。

请看图：

DFS此图的过程为：

1.首先任意找一个未被便利过的顶点，例如从V1开始，由于率先访问了它，所以需要标记V1即已经访问过。

2.然后遍历V1的邻接点，例如访问V2，并做标记，之后访问V2，V4，V8，然后V5。

3.当继续遍历V5的邻接点时，根据之前所做标记显示，所有邻接点都被访问过了。此时，从V5倒回来，看8是否有未被访问过的邻接点，如若没有。继续倒退。

4.通过DFSV1，找到 了一个未被访问的V3，继续遍历，然后访问V3，最后到V1，发现没有未被访问的。

6.最后一步需要判断是否所有顶点都被访问过，如果还有，再以剩下的点进行DFS。

所谓DFS，是从图中的一个顶点出发，每次遍历当前访问顶点的临界点，一直到访问的顶点没有未被访问过的临界点为止。然后采用依次回退的方式，查看来的路上每一个顶点是否有其它未被访问的临界点。访问完成后，判断图中的顶点是否已经全部遍历完成，如果没有，以未访问的顶点为起始点，重复上述过程。这是一个不断回溯的过程。

 

void dfs() { //参数用来表示状态
    if(到达终点状态) {
        ...//根据题意来添加
        return;
    }
    if(越界或者是不符合法状态)
        return;
    for(扩展方式) {
        if(扩展方式所达到状态合法) {
            ....//根据题意来添加
            标记；
            dfs（）；
            修改（剪枝）；
            (还原标记)；
            //是否还原标记根据题意
            //如果加上（还原标记）就是 回溯法
        }
    }
}

 

BFS（广度优先搜索）

广度优先搜索类似于树的层次遍历。从图中的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。类似于树的层次遍历。
最后还需要做的操作就是查看图中是否存在尚未被访问的顶点，若有，则以该顶点为起始点，重复上述遍历的过程。
还拿上图中的无向图为例，假设 V1 作为起始点，遍历其所有的邻接点 V2 和 V3 ，以 V2 为起始点，访问邻接点 V4 和 V5 ，以 V3 为起始点，访问邻接点 V6 、 V7 ，以 V4 为起始点访问 V8 ，以 V5 为起始点，由于 V5 所有的起始点已经全部被访问，所有直接略过， V6 和 V7 也是如此。
以 V1 为起始点的遍历过程结束后，判断图中是否还有未被访问的点，由于图 1 中没有了，所以整个图遍历结束。

 

#include<iostream>
#include<queue>
using namespace std;
const int INF = 100000000;
const int maxn = 10000;
typedef pair<int, int> P; //储存坐标下x,y
int maze[maxn][maxn];
int d[maxn][maxn];          //储存每个坐标的最短路径
int sx, sy;                 //起始坐标
int ex, ey;                 //终点坐标
int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };
int bfs() {
    queue<P> que;         //bfs用队列
    for (int i = 0; i < maxn; i++) {     //初始化所有距离为极大
        for (int j = 0; j < maxn; j++) {
            d[i][j] = INF;
        }
    }
    que.push(P(sx, sy));
    d[sx][sy] = 0;
    while (que.size()) {
        P p = que.front();
        que.pop();
        if (p.first == ex && p.second == ey)
            break;
        for (int i = 0; i < 4; i++) {
            int nx = p.first + dx[i];
            int ny = p.second + dy[i];
            if (nx >= 0 && nx < N && ny >= 0 && ny < N && d[nx][ny] == INF && maze[nx][ny] == ) {
                que.push(P(nx, ny));
                d[nx][ny] = d[p.first][p.second] + 1;
            }
        }
    }
    return d[ex][ey];
}

 

一世安宁