20162323周楠 2017-2018-1 《程序设计与数据结构》第九周学习总结
20162323周楠 2017-2018-1 《程序设计与数据结构》第九周学习总结
目录预览
0.教材学习内容总结
18.1 堆
-
Heap(堆)是一个除了底层节点外的完全填满的二叉树,底层可以不完全,左到右填充节点。
-
堆的每个元素都要大于或小于他的所有孩子
-
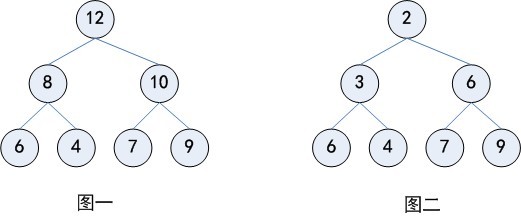
最大堆与最小堆
-
堆的三个基本操作:向堆中添加一个新元素、找到最大值和删除最大值
-
应用场景包括堆排序,优先队列等
一、向堆中添加一个新元素
- 方法:首先将这个元素添加为叶结点,然后将其向上移到合适的位置
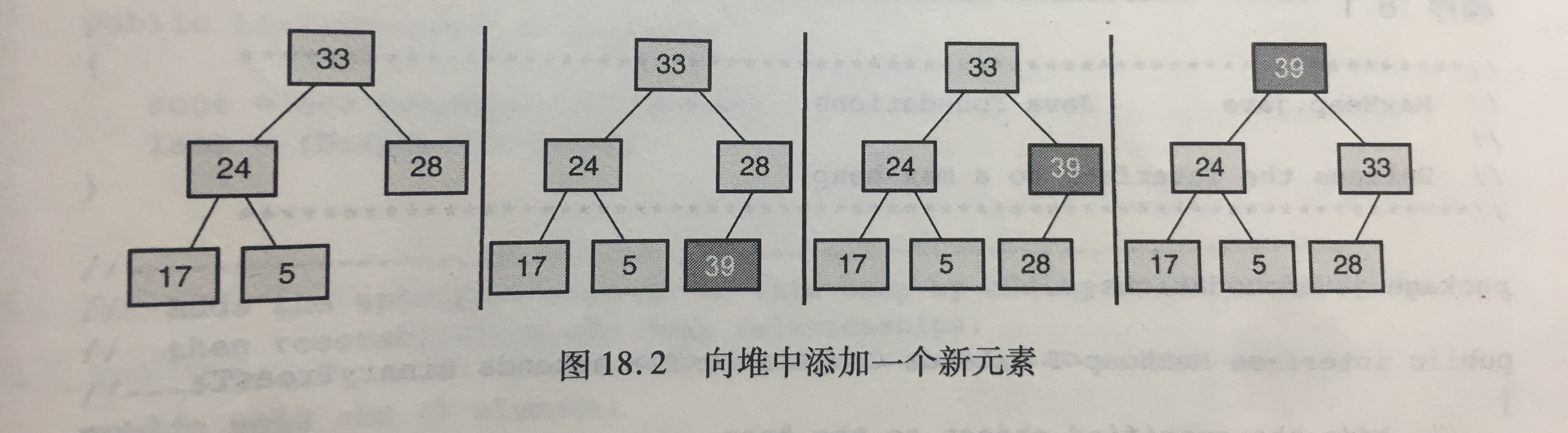
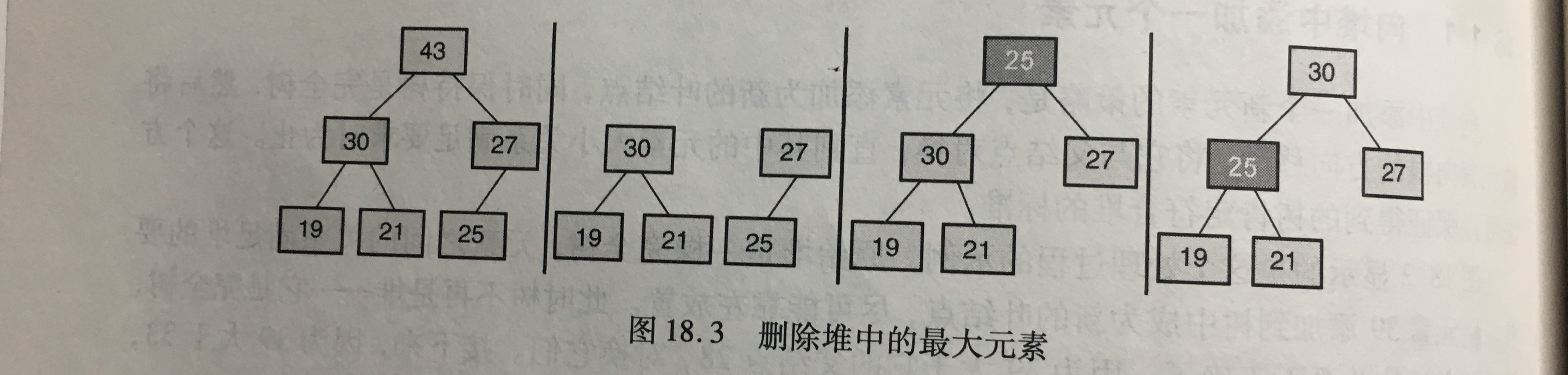
二、向堆中删除最大元素
- 方法:利用最后的叶结点取代根,然后将其向下移动到合适的位置
将新根与它的孩子进行比较,从而判定他是否需要向下移动。如果根元素小于它的较大孩子,则交换它们,继续这个过程,直到两个孩子都小于等于这个元素时为止
18.2 堆的实现
public interface MaxHeap<T extends Comparable<T>> extends BinaryTree<T>
{
// Adds the specified object to the heap.
public void add (T obj);
// 返回堆中具有最高值的元素的引用。
public T getMax () throws EmptyCollectionException;
// Removes and returns the element with the highest value in the
// heap.
public T removeMax () throws EmptyCollectionException;
}
定义接口
public
T removeMax() throws EmptyCollectionException {
if (root == null)
throw new EmptyCollectionException("Remove max operation " +
"failed. Tree is empty.");
T maxElement = root.getElement();
if (root.count() == 1) root = last = null;
else {
HeapNode <T> newLast = ((HeapNode <T>) root).getNewLastNode(last);
if (last.parent.left == last) last.parent.left = null;
else last.parent.right = null;
root.setElement(last.getElement());
last = newLast;
((HeapNode <T>) root).heapifyRemove((HeapNode <T>) root);
}
return maxElement;
}
public
void addElement(T node) {
}
//-----------------------------------------------------------------
// The following method is left as a programming project.
//-----------------------------------------------------------------
public
T getMax() throws EmptyCollectionException {
if (isEmpty()) {
throw new EmptyCollectionException ("Get max operation failed."+
"Heap is empty.");
}
return getRootElement();
}
18.3 堆排序
- 堆排序是先将一组元素一项项地插入到堆中,然后一次删除一个。
- 堆排序利用堆的基本特性对一组元素进行排序。
18.4 优先队列
- 优先队列是一个服从两个有序规则的集合
- 首先,具有更高优先级的项排在前面。其次,具有相同优先级的项按先进先出的规则排序。
- 优先队列不是FIFO队列。它根据优先级排列元素,而不是根据它们进入队列的次序来排列。
- 优先队列的应用:操作系统中的人物调度、网络中的交通调度及汽车修理工的的作业安排都是优先队列的例子。
1.教材学习中的问题和解决过程
- 问题:为什么有优先队列,但没有优先栈? - 解答:优先队列其实不是队列而是排序树或者堆(通常实现上),优先队列的队列跟那个先进先出队列所指的不是同一个东西。2.代码调试中的问题和解决过程
- 问题: