20162323周楠 2017-2018-1 《程序设计与数据结构》第七周学习总结
20162323周楠 2017-2018-1 《程序设计与数据结构》第七周学习总结
目录预览
0.教材学习内容总结
14.1 树的基本概念
- 树状图是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
- 树是非线性结构,其中的元素组织为层次结构。
- 树(由一组结点及一组边构成,结点用来保存元素,边表示结点之间的连接。每个结点都在树的某一层中。树的根是最顶层中唯一的结点,树中只有唯一的根结点。
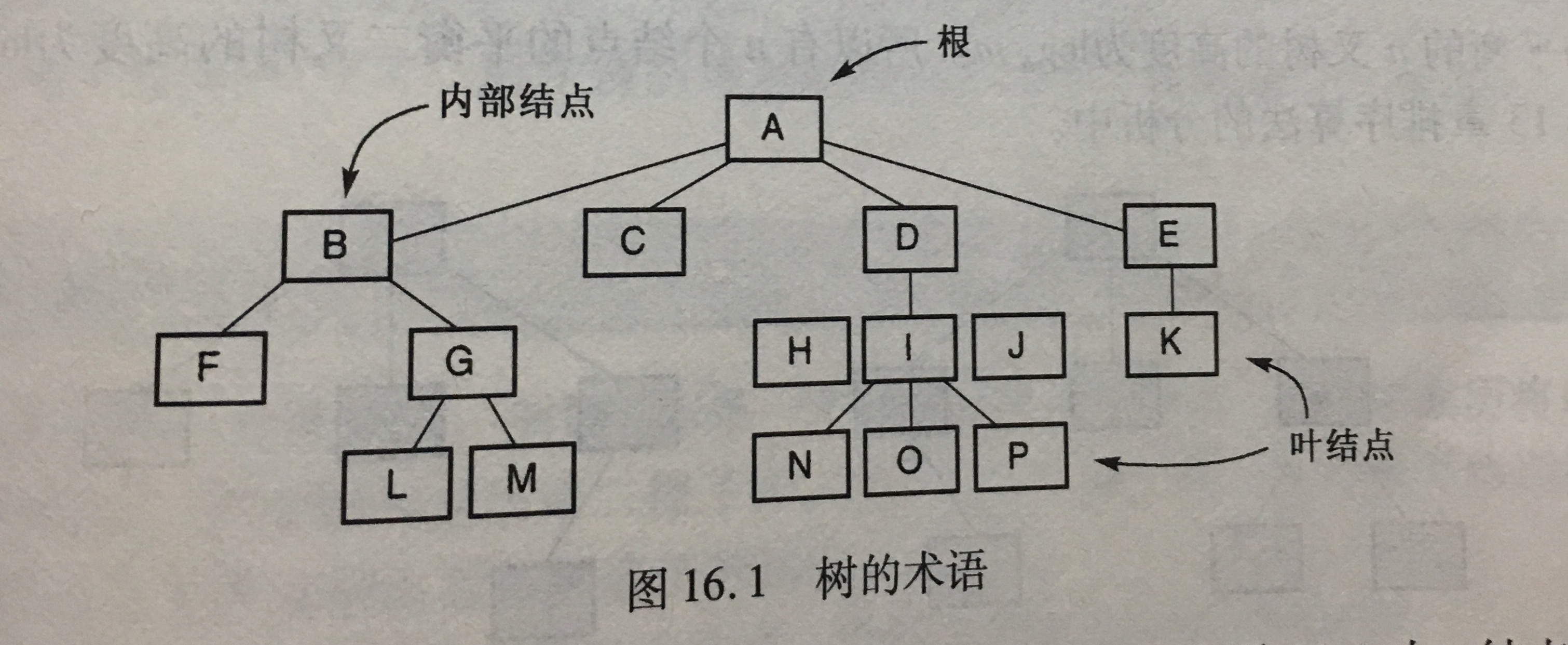
- 树(Tree):n(n≥0)个结点构成的有限集合。当n=0时,称为“空树”;对于任一棵“非空树”(n>0),它具备以下性质:
(1 )树中有一个称为“根(Root)”的特殊结点,用r表示;
(2)其余结点可分为m(m≥0)个“互不相交”的有限集T1,T2,...,Tm,其中每一个集合本身又是一棵树,称为原来树的“子树(SubTree)”。 - 根结点是树中唯一没有父结点的结点;树中构成另一棵树结构的部分称为子树;
- 结点的度(Degree):结点的子树个数;
- 树的度:树的所有结点中最大的度数;
- 叶结点(Leaf):没有任何子结点的结点;
- 父结点(Parent):有子树的结点是其子树的根节点的父结点;
- 子结点/孩子结点(Child):树中较低一层的结点称为前一层结点的子结点,若A结点是B结点的父结点,则称B结点是A结点的子结点;
- 一个结点只能有一个父结点,但一个结点可以有多个子结点。
- 兄弟结点(Sibling):具有同一个父结点的各结点彼此是兄弟结点;
- 至少有一个子结点的非根节点称为内部结点
- 路径(Path)和路径长度(Path length ):从根开始沿着父结点到子结点的边向下,得到树中的一条路径,结点的层是从根到该结点的路径长度,而路径长度为根到该结点的路径上的边数。
- 高度(height;或深度,depth):树中从根到叶结点的最长路径的长度;
- 祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点;
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙;
- 结点的层次(Level):规定根结点在1层,其他任一结点的层数是其父结点的层数加1。
一、树的分类
其中重要的一种方法是按树中任意结点的最大子结点个数来分,这个值有时称为树的度(Order)。
- 树的度表示树中任意结点的最大子结点数
1.二叉树(Binary Tree):每个结点最多有两个子结点的树
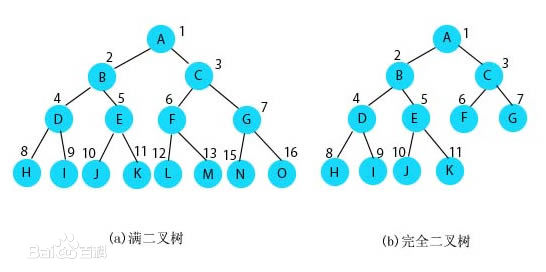
- 满二叉树(Full Binary Tree)/ 完美二叉树(Perfect Binary Tree):除最后一层无任何子结点外,每一层上的所有结点都有两个子结点的二叉树。
- 完全二叉树(Complete Binary Tree):有n个结点的二叉树,对树中结点从上至下、从左到右顺序进行编号,编号为i(1≤i≤n)结点与满二叉树中编号为i结点在二叉树中的位置相同。
另一种方法是看树是否平衡,如果树的所有子结点都在同一层上,或彼此最多不超出一层,则认为这个树是平衡的。

- 有m个元素的平衡n叉树的高度是lognm,有n个结点的平衡二叉树的高度是log2n。
二、树的遍历
树有4种遍历方法,是先序、中序、后序、层序
- 先序遍历(preorder traversal):
1.访问根结点
2.访问左子树
3.访问右子树

- 中序遍历(inorder traversal):
1.访问左子树
2.访问根结点
3.访问右子树
原则:访问左子树。【先访问左子树中的左子树,再访问左子树中的右子树。】直到访问到叶子结点后输出。
输出根。
访问右子树。【先访问右子树中的左子树,再访问右子树中的右子树。】直到访问到叶子结点后输出。

-
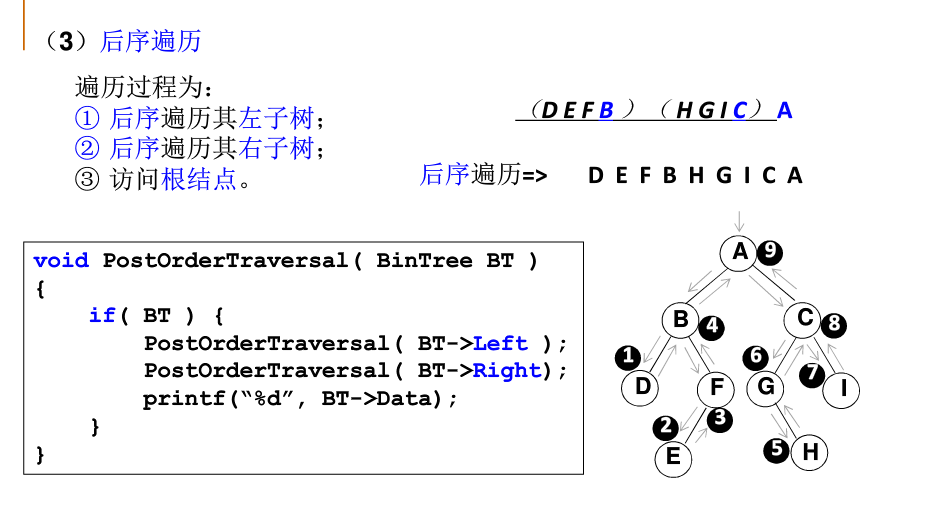
后序遍历(postorder traversal):
1.访问左子树
2.访问右子树
3.访问根
原则:访问左子树。【先访问左子树中的左子树,再访问左子树中的右子树】。直到访问到叶子结点后输出。
访问右子树。【先访问右子树中的左子树,再访问右子树中的右子树】。直到访问到叶子结点后输出。
再返回访问根,并输出。
- 层序遍历:每层上的结点自左至右地访问

16.3 树的实现策略
一。在数组中计算链
- 使用数组实现二叉树时,位于位置n的元素的左孩子在(2n+1)的位置,其右孩子在(2*(n+1))的位置
二。在数组中保存链
- 树的基于数组的存储链实现方式可以占据数组中的连续位置,不管树是不是完全树
三、链式结点
- 用一个引用数组或是引用链表来保存各子结点的引用,而不是使用单独的引用来保存
16.4 二叉树的实现
- 如何在一般二叉树中添加和删除元素,要取决于树的用途
// 返回存储在树根中的元素。
public T getRootElement() throws EmptyCollectionException;
// 返回根的左子树。
public BinaryTree<T> getLeft() throws EmptyCollectionException;
// 返回根的正确子树。
public BinaryTree<T> getRight();
// 如果二叉树包含与指定元素匹配的元素,则返回true,否则返回false。
public boolean contains (T target);
// 返回对与指定目标匹配的树中的元素的引用。
public T find (T target) throws ElementNotFoundException;
// 如果二叉树不包含元素,则返回true,否则返回false。
public boolean isEmpty();
// 返回此二叉树中的元素数。
public int size();
// 返回二叉树的字符串表示形式。
public String toString();
// 返回二叉树上的预订遍历。
public Iterator<T> preorder();
// 返回二叉树上的无序遍历。
public Iterator<T> inorder();
// 返回二叉树上的后期遍历。
public Iterator<T> postorder();
// 在二叉树上执行级别遍历。
public Iterator<T> levelorder() throws EmptyCollectionException;
没有定义向树中添加和删除元素的方法。
16.5 决策树
- 结点表示判定点,结点的孩子表示那一刻可用的选择,决策树的叶结点
- 一棵带yes-or-no问题的简单的决策树可用一棵二叉树来表示
- 使用决策树可以设计专家系统(专家系统:表示特定领域专家知识的一种软件系统)
1.教材学习中的问题和解决过程
- 问题:树的实现策略 - 解答:属于线程,一个线程一个栈,一个方法调用就是一个入栈,调用结束就是出栈,跟实例没有关系,用数组来实现二叉树,树上的元素存放位置在数组中是固定的,如果树的i位置(从0开始按层编号)有元素,就放在数组的i号位置,没有元素,数组对应的位置就空着。i的左右子树的编号为2i+1和2i+2。
2.代码调试中的问题和解决过程
- 问题: