博客作业05--查找
1.学习总结(2分)
1.1查找的思维导图
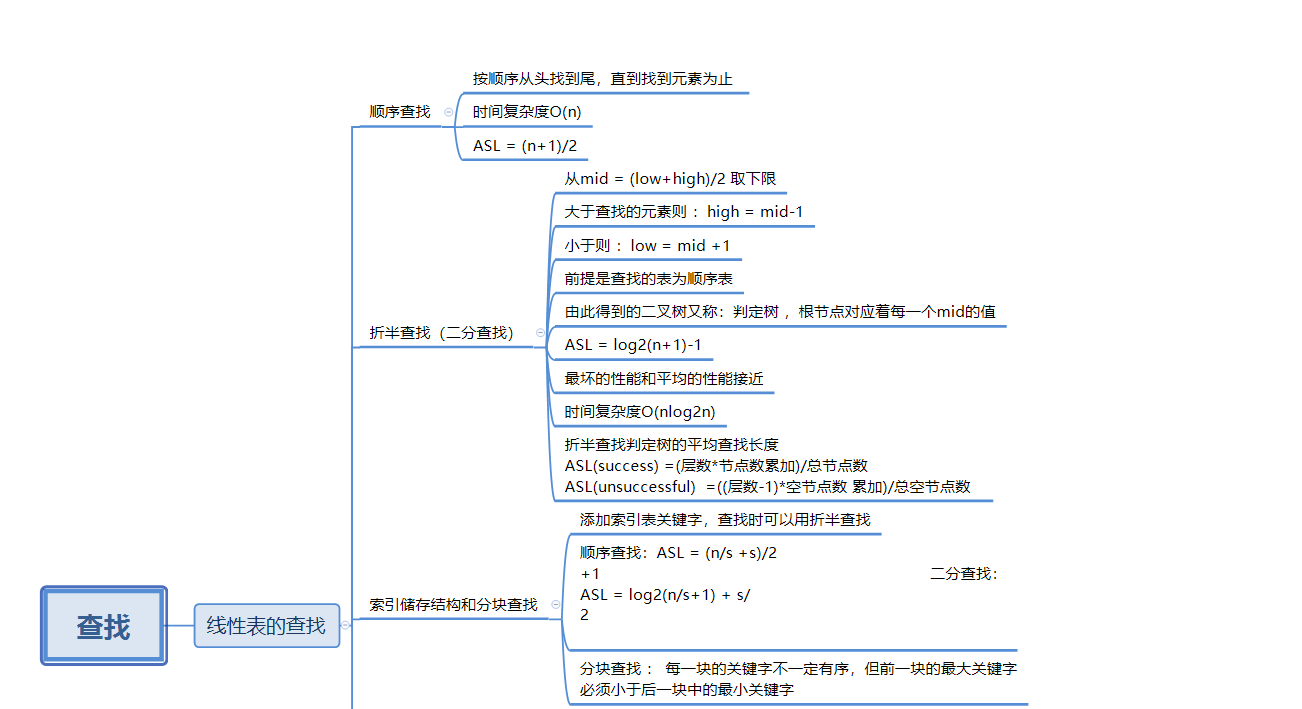

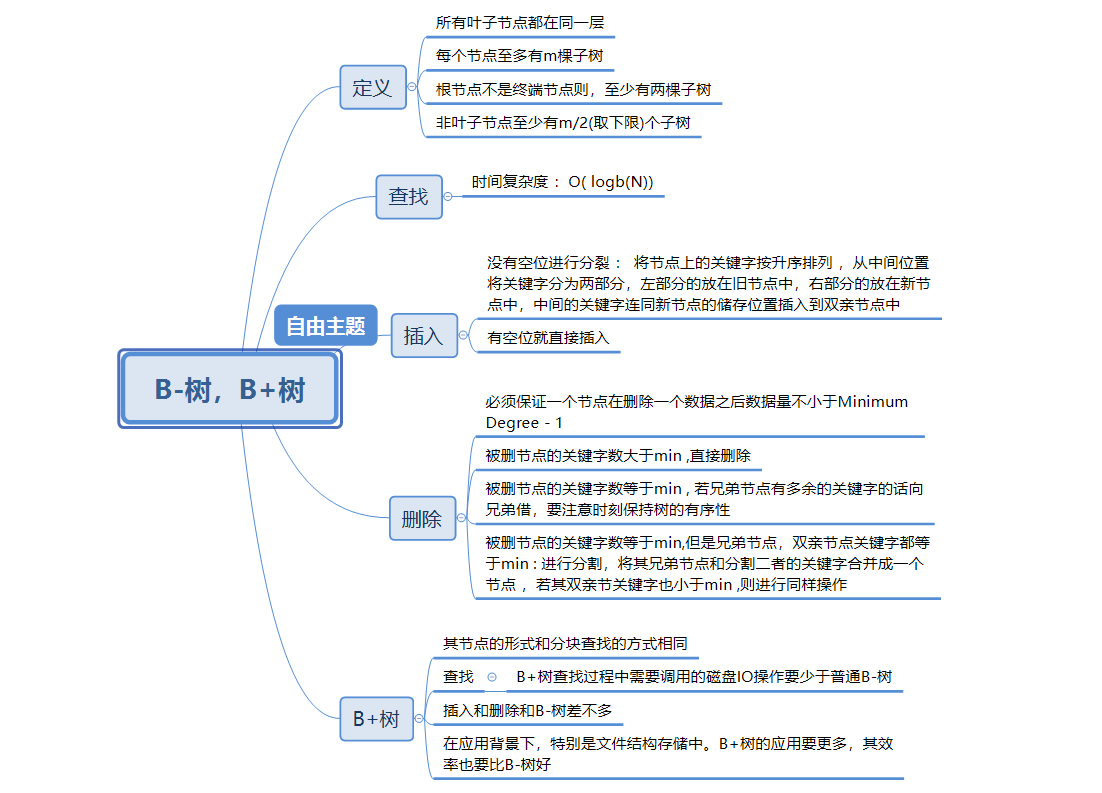
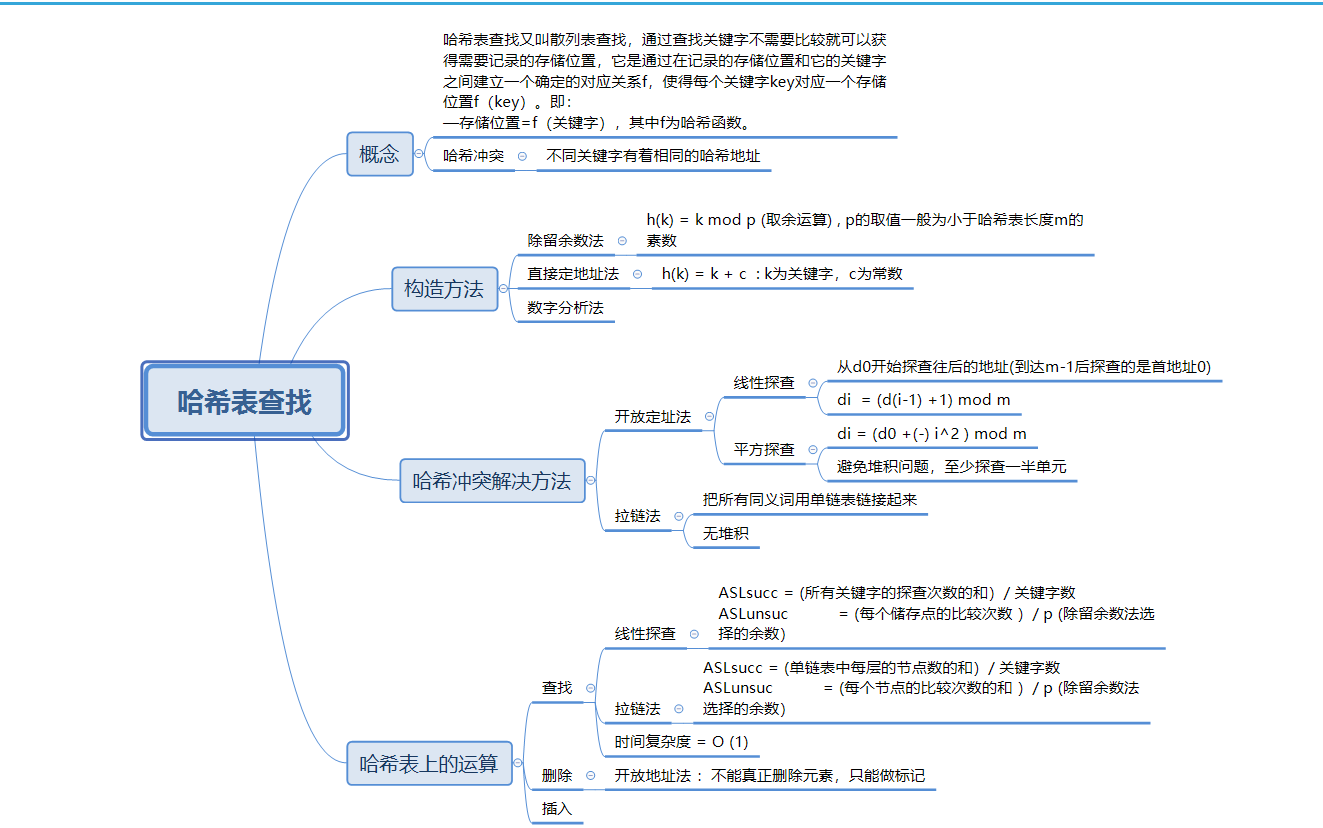
1.2 查找学习体会
查找这块操作和代码量比较多,需要花时间去记,很烦 。。
使用STL容器,让相同数据的累加不需要将数组初始化,直接进行累加,查找输入的数据是否已经存在也只需要一个语句就可以完成,代码简短了许多 , 用STL容器查找用数组的形式,将字符串设为数组地址,查找时直接用字符串查找。
第一种:用count函数来判定关键字是否出现,其缺点是无法定位数据出现位置,由于map的特性,一对一的映射关系
,就决定了count函数的返回值只有两个,要么是0,要么是1,出现的情况,当然是返回1了
第二种:用find函数来定位数据出现位置,它返回的一个迭代器,当数据出现时,它返回数据所在位置的迭代器,
如果map中没有要查找的数据,它返回的迭代器等于end函数返回的迭代器,
2.PTA实验作业(4分)
2.1 题目1:6-3 二叉搜索树中的最近公共祖先
2.2 设计思路(伪代码或流程图)
int LCA( Tree T, int u, int v )
{
如果树为空
返回 ERROR ;
如果 u,v不在数组内
返回 ERROR ;
如果 u或v有等于T->key
返回T->key
如果一个在根节点左边一个在根节点右边
返回T->key
如果 u比T->key大 递归调用右子树
如果 u比T->key小 递归调用左子树
}
int Search(Tree T , int u) //查找元素是否存在于树内
{
如果树空
返回 0
如果找到则返回 1
如果大于T->key
递归调用右子树
如果小于T->key
递归调用左子树
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。
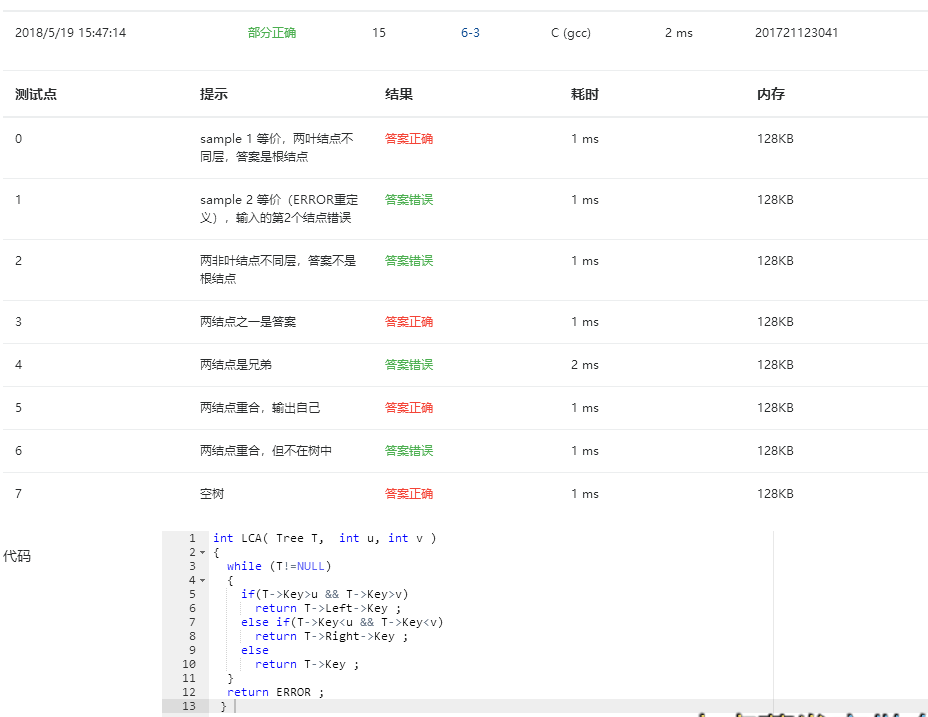
只考虑一个大于根节点,一个小于根节点的情况和两个都小于根节点,两个都大于根节点情况 ,没有考虑到节点不在树内和节点不同层情况
增加了一个寻找元素是否在树内的函数 ,解决
2.1 题目2:7-1 QQ帐户的申请与登陆
2.2 设计思路(伪代码或流程图)
map<string,int>p; 储存账号 和密码
string ch,number,str; //ch是新老用户 ,number是账号 , str是密码
输入指令次数n
while (n-- )
{
输入x,y,z ;
如果是老用户
{
判断它是否存在 if(iter != mapStudent.end())
不存在则printf("ERROR: Not Exist\n");
存在则判断密码是否正确if(mapStudent[number]==str)
正确输出printf("Login: OK\n")
错误输出printf("ERROR: Wrong PW\n")
}
如果是新用户
{
判断是否已经存在if(iter != mapStudent.end())
存在则输出printf("ERROR: Exist\n");
不存在的话mapStudent[number] = str记录下密码 ; printf("New: OK\n");
}
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。
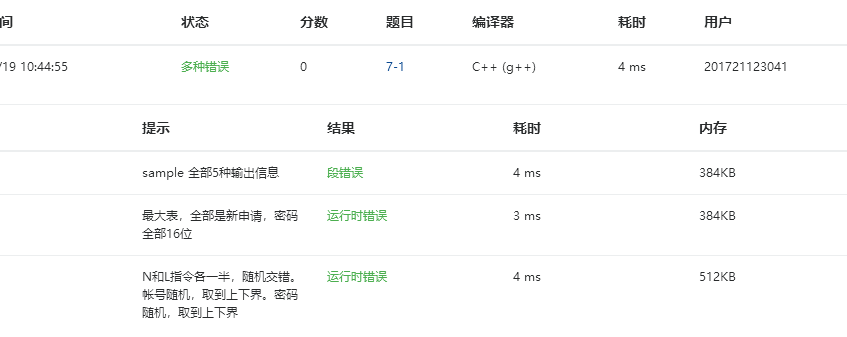
可能是这个语句出问题

后来改为mapStudent[number] = str ; 插入元素
2.1 题目3:7-2 航空公司VIP客户查询
2.2 设计思路(伪代码或流程图)
定义字符串数组储存身份证 char identity[21] ;
map<string , long long >customers ;储存客户信息
输入顾客数n 和最低旅程 k
while (n--)
{
输入身份证和里程数
当mile小于k时令mile = k ;
累加里程数customers[identity] += mile ;
}
输入查询人数n
while(n--)
{
判断是否存在if(iter != customers.end())
当该顾客存在时输出他的里程数
不存在时输出No Info
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
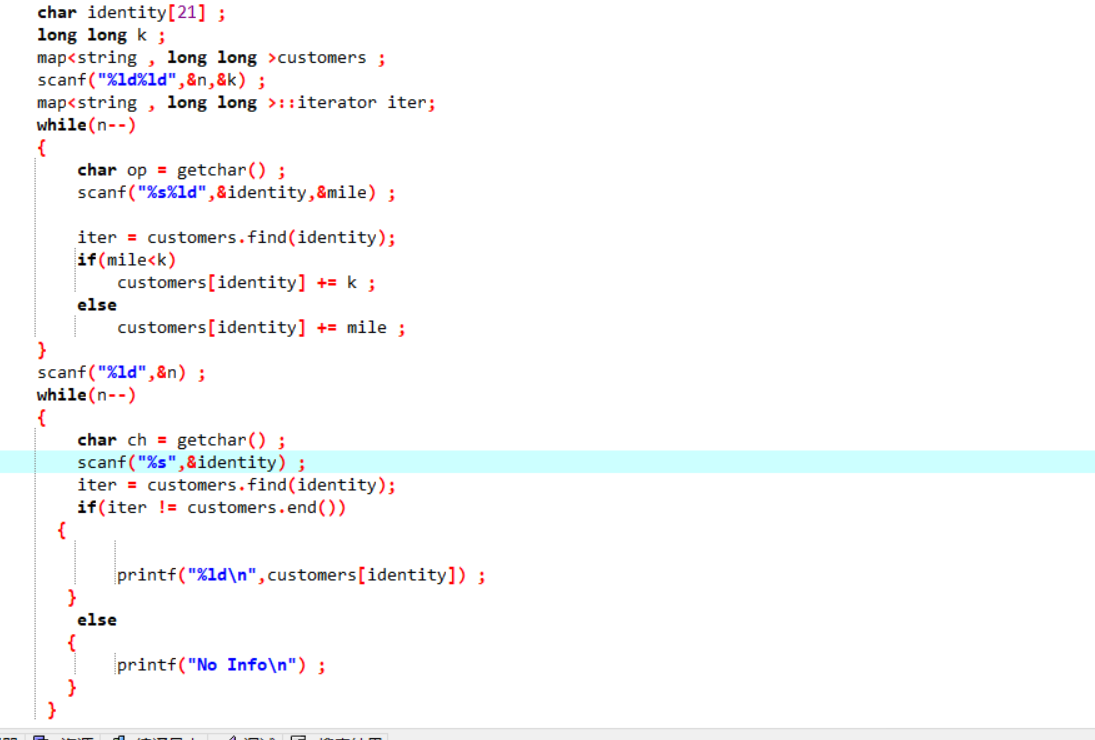
2.4 PTA提交列表说明。
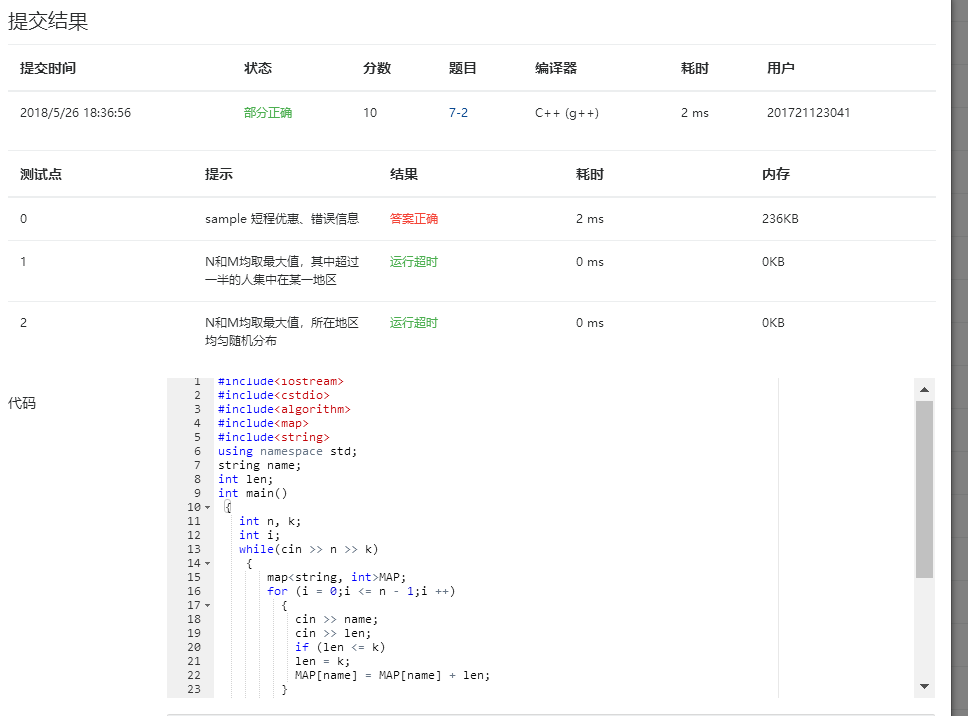
开始输入用户身份证用的是string 型 ,导致错误,后来改为字符串数组
,还有将cin,cout改为scanf和printf,才通过
3.截图本周题目集的PTA最后排名
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分 : 2.5
4. 阅读代码(必做,1分)
埃拉托斯特尼筛法
Count the number of prime numbers less than a non-negative number, n
//http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
class Solution {
public:
int countPrimes(int n) {
if(n < 2)
return 0;
vector<int> isPrime(n,1);
isPrime[0] = 0;
isPrime[1] = 0;
int count = 0;
for(int i = 2;i<n;++i)
{
if(isPrime[i] == 1)
{
++count;
if(i>sqrt(n))
continue;
for(int j = i*i;j<n;j+=i)
{
isPrime[j] = 0;
}
}
}
return count;
}
};
中心思想就是,从2的倍数开始,反复的将素数的倍数标记为非素数。
给定的一个素数p的倍数构成一个从p开始的序列,相邻元素之间的差值为p。这是筛法与一般方法的关键区别
5. 代码Git提交记录截图