博客作业04--树

1.学习总结(2分)

1.1树结构思维导图

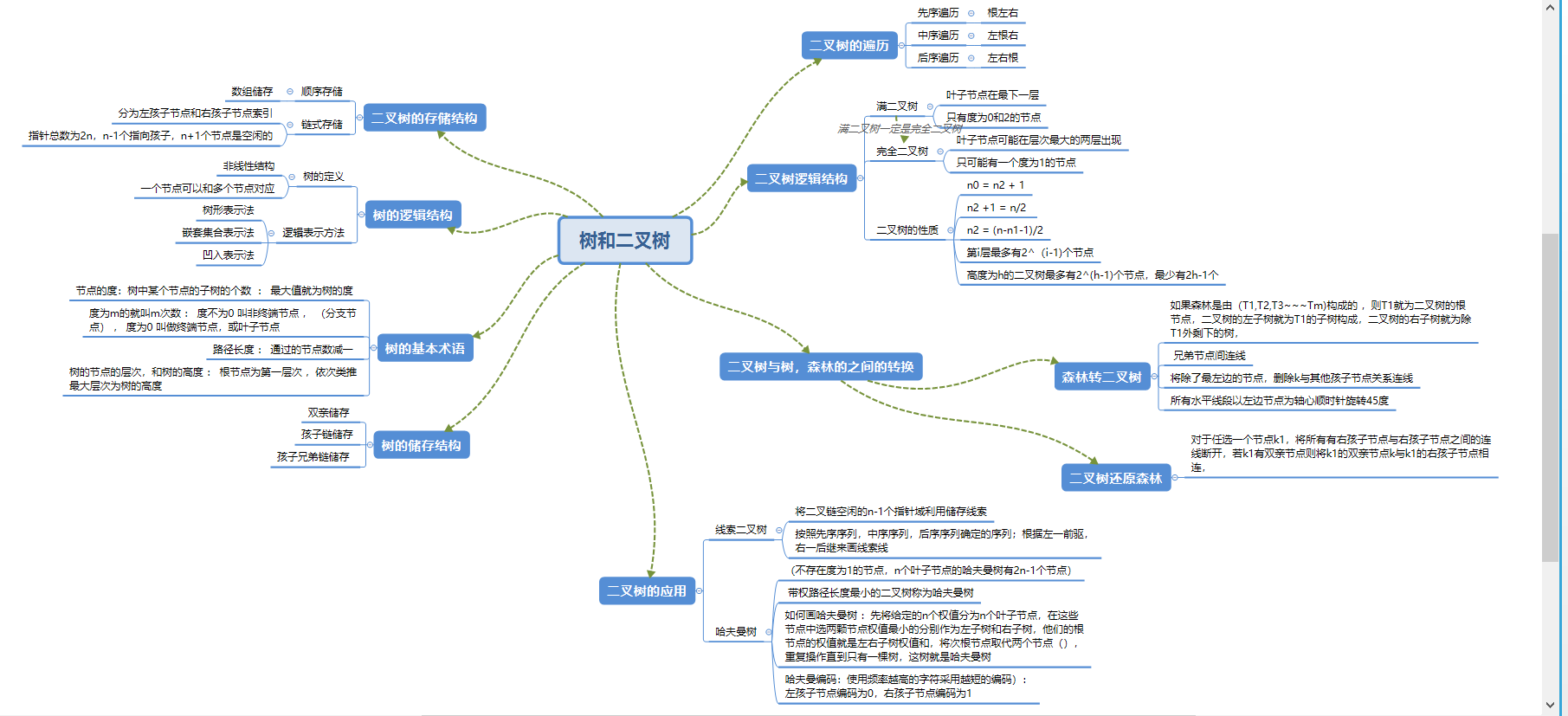
1.2 树结构学习体会

对于树的递归做法看着简单，自己写的话很难下手
树的性质还没有记牢
运用树来解题还是有困难，要多加学习

2.PTA实验作业（4分）

2.1 题目1：6-4 jmu-ds-表达式树

2.2 设计思路（伪代码或流程图）

当数组不空时
    判断是否为运算符不是则
        建立新的节点，将此时的字符赋给节点，并将节点入栈
    是则
        判断该字符与栈顶字符的优先级
            大于则将其入栈
            等于将栈顶元素出栈
            小于则将栈顶元素赋予根节点，并将栈的接下来两个元素赋给根节点的左右孩子，将根节点入树栈

当栈不为空时
    取栈顶元素为新建根节点值，，根节点的右孩子，左孩子依次取接下来的栈顶元素
    将根节点入树栈
    
将树栈顶的根节点符给T

//计算表达式树

将树中的数字字符转为数字
x保存递归左子树的值
y保存递归右子树的值
判断运算符
    + 则 返回x+y
    -  则 返回x-y
    * 则 返回x*y
    /  则 当分母不为0 时再返回x/y

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

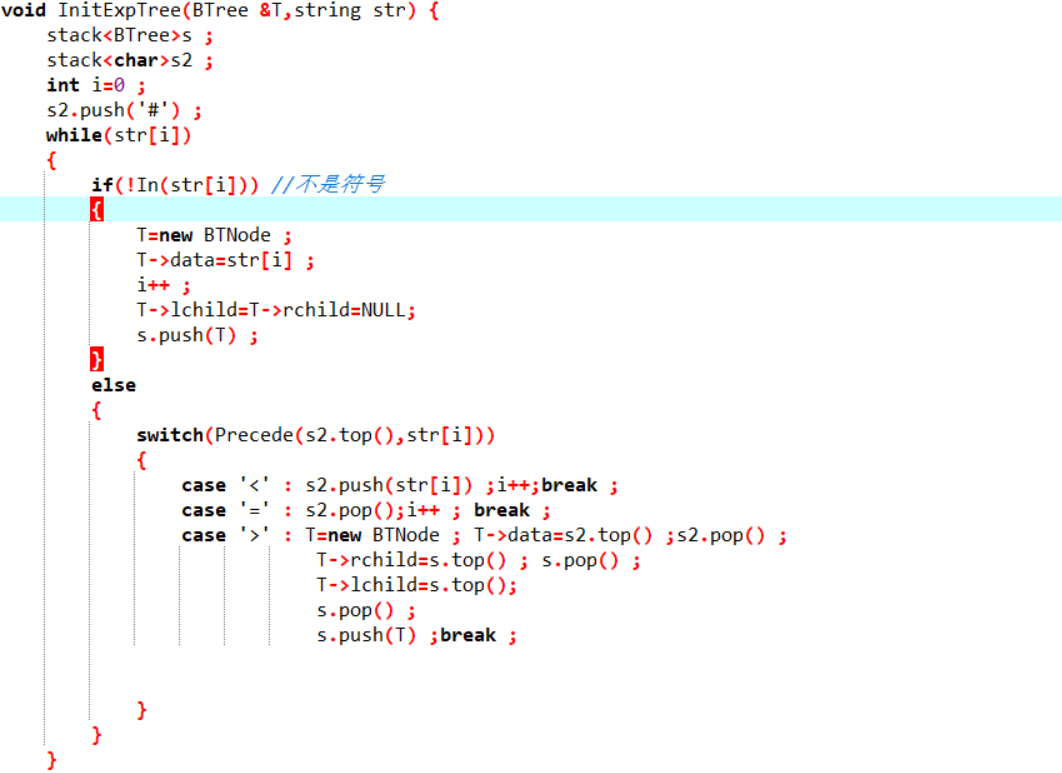
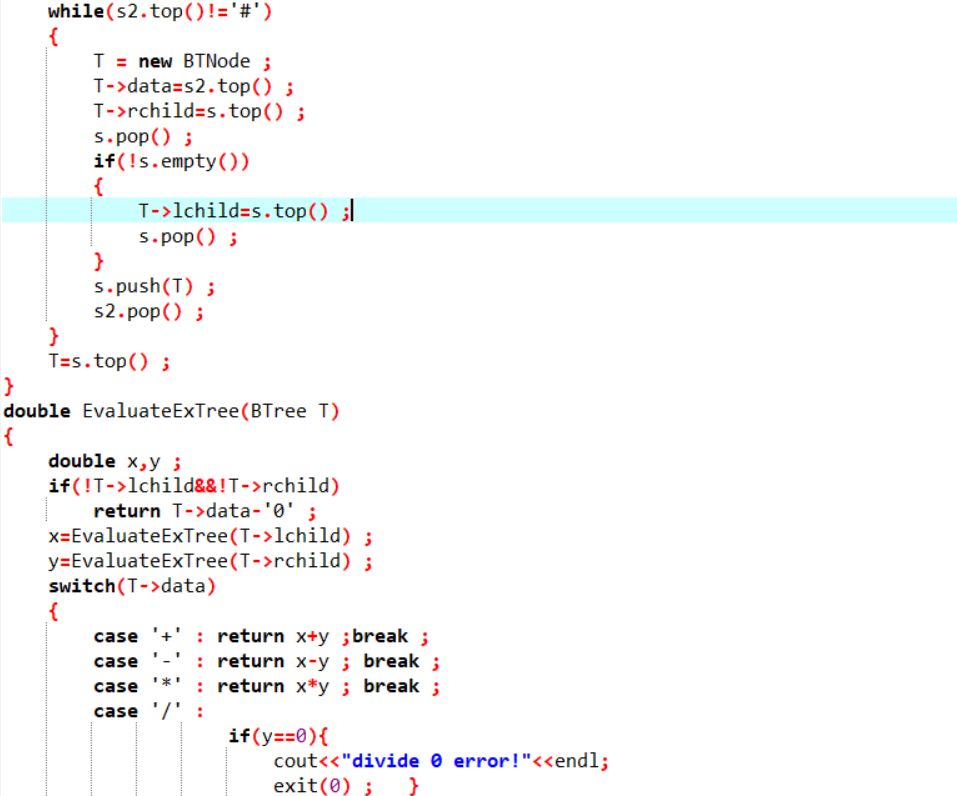
2.4 PTA提交列表说明

将所有代码提交编译错误，

2.1 题目2：7-1 还原二叉树

2.2 设计思路（伪代码或流程图）

*pre为先序序列，*in为中序序列
创建二叉树节点b
for p=in to in+n
    在中序序列中找等于*pre的节点位置k
确定根节点在中序序列中的位置k =p-in
递归构造左子树每次返回先序序列进1，将中序节点分割开，b->lchild=CreateBTree(pre+1,in,k)  
递归构造右子树b->rchild=CreateBTree(pre+k+1,p+1 ,n-k-1) 

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明

2.1 题目3：7-3 jmu-ds-二叉树层次遍历

2.2 设计思路（伪代码或流程图）

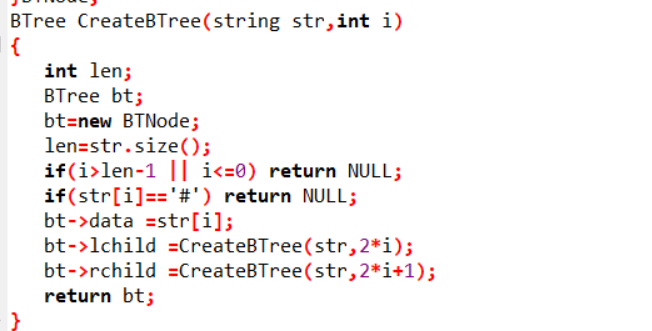
递归法创建树BTree CreateBTree(string str,int i)
创建根节点bt
求字符串长度len
当i大于len时返回NULL
如果根节点为#返回NULL
根节点值为str[i] , 
递归创建孩子节点，左孩子节点为2i ,右孩子节点为2i+1
bt->lchild =CreateBTree(str,2*i); 
bt->rchild =CreateBTree(str,2*i+1); 
//层次遍历 
    如果根节点为空，返回NULL
    不为空则将b进队
    当队列不为空时
        p= 队头元素，出队
        输出p的值，
     当左孩子不为空时
        输出左孩子值
    当右孩子不为空是
        输出右孩子值

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的得分 ： 2分

4. 阅读代码（必做，1分）

void levelnumber(BTNode *b，int h，int a[])
{
 if (b==NULL)   return;
 else
  {
	a[h]++;
	levelnumber(b->lchild，h+1，a);
	levelnumber(b->rchild，h+1，a);
  }
}
int fun(BTNode *b)
{     
    int width=0，i;   
    int a[MaxSize];
  for (i=1;i<MaxSize;i++)   a[i]=0;		//a设置所有元素初始化为0
  levelnumber(b，1，a);
  i=1;
  while (a[i]!=0)	
  {      
        if (a[i]>width)   width=a[i];
	 i++;
  }
      return width;
 }

功能求二叉树的最大宽度 ， 利用数组记录下每一层的节点数，数组的下标就为层数 ， 方便记录，索引

5. 代码Git提交记录截图