面向程序员编程——精研排序算法
这篇文章很长,我花了好久的时间(中间公司出了bug,加班了好几天( ¯ ¨̯ ¯̥̥ ))进行整理,如有任何疑问,欢迎随时留言。
关键字:排序算法,时间复杂度,空间复杂度
排序就是研究如何将一系列数据按照某种逻辑顺序重新排列的一门算法。在计算机早期,排序要占用大量计算资源是人们的共识,而今天随着机器性能的提高,以及排序算法的演进,排序已经非常高效,现在随处都会提起数据的重要性,而整理数据的第一步就是排序。
引用自知乎:很多东西的难度,是随着需求变化的。比如排序吧,10个数字,我可以给你人眼排序,
100个可以冒泡排序,学过c语言的大一学生,就能干,免费。100T的数字呢?你给我冒个泡试试?量变产生了质变,数据量的增大,让本来可用的算法变得不可用,因为你找不到100T这么大内存,n2复杂度的冒泡排序让排序时间变得不可接受。100T数据排序已经是各大公司炫耀技术的方式了。腾讯打破2016 Sort Benchmark 4项纪录,98.8秒完成100TB数据排序,现在你告诉我,排序这个事儿简不简单?
综上所述,排序是编程的基础,每一名优秀的程序员都值得熟悉和掌握,今天我来总结一下。
首先介绍几个基础概念,曾经我们面向高考学习的时候都学过,只不过现在可能忘掉了,没关系,下面我们重新介绍一下:
- 对数函数
在数学中用log表示,
log2^8 = 3
其中8是真数,2是对数的底,3是对数。我们都知道2的3次方等于8,对数函数相当于求2的几次方等于8?
对数函数的表示还有几个特殊情况,当底为10时,log可以表示为lg,同时省略底10
lg100 = 2
称以无理数e(e=2.71828...)为底的对数称为自然对数(natural logarithm),并记为ln。
- 时间复杂度
时间复杂度是定性的描述了一段程序的运行时间,
官方定义:算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度(O是数量级的符号 ),简称时间复杂度。
讲人话:算法中某个特定步骤的执行次数 / 对于总执行时间的估算成本,随着「问题规模」的增大时,增长的形式。
时间复杂度使用大写字母O来表示。
在长度为N的数组中,如果次数与N的大小无关,始终为一个固定的次数,或许是1次,或许是3次,它们都记为O(1),也叫常数阶,一个遍历就是O(N),也叫线性阶,嵌套两个遍历就是 O(N^2),也叫平方阶, 同样的嵌套三个遍历就是O(N^3 ),也叫立方阶。
常见的时间复杂度如下图:
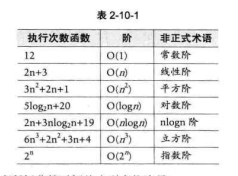
若程序中包含一个嵌套两个遍历的函数,还有一个嵌套三个遍历的函数,那就是O(N^2) + O(N^3) 当问题规模增大到无限大的时候,较小的分子一方可以忽略,按照数量级大的来,仍旧是O(N^3) 。
如果有二分分治,那就是O(log2^N) 。
如果一个遍历嵌套一个二分,则是O(N*log2^N)。
- 空间复杂度
空间复杂度是指算法在执行过程中临时占用内存的量度,空间复杂度仍旧使用大写字母O来表示。一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。
在正无穷的“问题规模”时(n = +∞),时间复杂度和空间复杂度较低的程序的运行时间一定小于复杂度较高的程序。所以,时间复杂度和空间复杂度共同决定了程序的执行效率。
下面进入代码阶段。
我们先创建一个java工程sort,然后创建一个抽象类Sort。代码如下:
package algorithms.sort;
import java.util.Random;
public abstract class Sort {
private int count;
protected int[] sort(int[] array) {
return null;
};
/**
* 互换位置的方法
*
* @param array
* 要换位置的目标数组
* @param i
* 数组位置1
* @param j
* 数组位置2
* @return 换好位置以后的数组
*/
protected int[] swap(int[] array, int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
count++;
return array;
}
protected void show(int[] array) {
for (int a : array) {
System.out.println(a);
}
System.out.println("数组长度:" + array.length + ",执行交换次数:" + count);
}
public int[] getIntArrayRandom(int len, int max) {
int[] arr = new int[len];
Random r = new Random();
for (int i = 0; i < arr.length; i++) {
arr[i] = r.nextInt(max);
}
return arr;
}
/**
* 取得数组的最大值
*
* @param arr
* @return
*/
protected int max(int[] arr) {
int max = 0;
for (int a : arr) {
if (a > max)
max = a;
}
return max;
}
}
然后再创建一个客户端Main,用来调用算法。代码如下:
package algorithms.sort;
public class Main {
public static void main(String[] args) {
Sort s = new XXXSort();
int[] array = s.getIntArrayRandom(32, 120);
array = s.sort(array);
s.show(array);
}
}
其中XXXSort类就是我们接下来要介绍的十种排序算法。
冒泡排序
简单来讲,在一个长度为n的数组中,对每两个相邻的数进行比较,将数值较大的(或者比它小的)换到右侧位置,遍历一遍以后,第一个数已经换来换取换到了最适合它的位置k,同时,在[k,n]之间又可能会出现大于等于0个数被换来换去换到了最适合他们的位置。然后再从头对每两个相邻的数进行比较,以此类推,直到将所有的数均换到了最适合他们的位置为止。
时间复杂度为:
T(n) = O(n^2)
空间复杂度为:
S(n) = O(1)
这里的空间复杂度只有在交换时的一个中转临时变量占用的内存空间,所以是O(1)。
具体实现代码如下:
package algorithms.sort;
public class BubbleSort extends Sort {
public int[] sort(int[] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length - 1; j++) {
if (array[j] < array[j + 1]) {
array = swap(array, j, j + 1);
}
}
}
return array;
}
}
数组长度总共32, 执行交换次数:238
仔细想一下,会觉得这里面交换次数很多,随着数组长度N的变大,无效交换的比重会越来越大,而且这里面的比较,有很多是重复的,例如在第一层循环第二遍执行时,很多已经找到自己在数组中合适位置的数仍旧参与比较,这些比较就是无意义的。
但是,冒泡这个思想却是排序算法比较里程碑的,所以放在第一个进行介绍。
选择排序
冒泡排序的优化,找到每个位置合适的数。例如,第一个位置,遍历找出最小(或者最大)的一个数放在这,然后是第二个位置放第二小的数,以此类推,找到每个位置合适的值以后再进行交换,比起冒泡排序,降低了交换的次数,但是由于都是嵌套两层循环,时间复杂度相同,空间复杂度也为O(1),原理同上。
package algorithms.sort;
public class SelectSort extends Sort {
public int[] sort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {// 控制交换的次数,最多交换n-1次。
int maxIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] > array[maxIndex]) {
maxIndex = j;
}
}
if (maxIndex != i) {// 找到当前位置后面最小值的位置,交换。
swap(array, maxIndex, i);
}
}
return array;
}
}
数组长度总共32, 执行交换次数:27
相同的数组,选择排序的交换次数为27(这里最多不超过31次),而冒泡排序是238,可以看出,选择排序的交换次数大大减小,如果在问题规模n为正无穷的时候,这个交换次数如果很小的话可以大大降低磁盘的I/O操作,而获得相同的排序结果。所以选择排序虽然在时间复杂度和空间复杂度均与冒泡排序相同,但是它在I/O的表现上非常出色。
插入排序
插入排序是首先将第一个数字当做一个已有序的新数组,(数组里面只有一个数字,肯定算有序)从第二个数字开始,将其与数组已有元素(从最右侧开始比)进行比较,然后插入到该新数组中适合的位置。
例如打扑克,摸牌阶段的码牌动作,第一张摸过来,不动(已有序),第二张摸过来,跟第一张牌比较一下,如果比它大就插到第一张的前面,小则插到后面,第三张摸过来,先跟第二张比较一下,如果比它大就再跟第一张牌比较,如果比它们都大就插到第一张牌的前面(前面再也没有牌了,不用比了,就是下面代码中的j>0终止条件)。而如果不比第一张牌大,就保留插入到第二张的前面,而此时第二张在它与刚摸到的这张牌比较完的时候就已经成为了第三个位置的牌了。以此类推,代码如下。
package algorithms.sort;
public class InsertSort extends Sort {
public int[] sort(int[] array) {
// 从第二张牌开始比较
for (int i = 1; i < array.length; i++) {
int target = array[i];
int j = i;
// 如果比前一个大,就把前一个放到当前目标牌的位置,把前一个的位置空出来,然后继续跟更前一个比较,循环去找到最准确的目标位置
while (j > 0 && target > array[j - 1]) {
array[j] = array[j - 1];
j--;
}
// 在目标位置的插入操作
array[j] = target;
}
return array;
}
}
数组长度总共32, 执行交换次数:0
上面两种排序算法都是采用交换位置的方式,而插入排序是采用插入的方式,没有发生交换操作,所以交换次数为0。
插入排序的比较次数与选择排序差不多,只不过选择排序是不断与当前位置后面的元素比较,而插入排序是不断地与当前元素前面的比。按照最坏的打算,每一次跟前面的牌比较都是要比到第一位为止,也就是说本身数组就是一个有序数组,利用该排序更换排序方式时,会发生这种最坏情况。
假设数组的长度为N,第一层循环的第一次操作是执行1次,第二次操作是执行2次,直到第N-1次操作是执行N-1次,那么总次数为一个等差数列求和,即N*(N-1)/2,当问题规模扩大到无穷大时,小数量级的加减可以忽略,同时原分母2可以忽略不计,最终时间复杂度仍旧为O(N^2),空间复杂度也为O(1),原理同上。
快速排序
快速排序是最流行的排序算法,效率是比较高的。它是基于冒泡排序,但略比冒泡排序复杂,基本思想为二分分治,将一个数组按照一个基准数分割,比基准数小的放基准数的右边,大的放在左边。这就需要定义两个数组下标变量,分别从数组的两头开始比较换位,最终在数组的中间位置相遇,然后在基准数的左边和右边再递归执行这个分割法即可,代码如下。
package algorithms.sort;
public class QuickSort extends Sort {
public int[] sort(int[] array) {
return quickSort(array, 0, array.length - 1);
}
/**
* 分割的方法
*
* @param array
* @param left
* [left, right]
* @param right
* @return 两情相悦的位置
*/
private int partition(int[] array, int left, int right) {
int pivot = array[left];// 定义基准数
int pivotIndex = left;// 保存基准数的位置
while (left < right) {// 直到中间相遇为止
while (left < right && array[right] <= pivot)// 在右侧找到第一个比基准数大的
right--;
while (left < right && array[left] >= pivot)// 在左侧找到第一个比基准数小的
left++;
swap(array, left, right);// 互换上面找到的第一个比基准数大的和第一个比基准数小的位置
}
swap(array, pivotIndex, left);// 最后交换基准数到两情相悦的位置(不一定是中间)。
return left;
}
/**
* 一到递归别迷糊:用于递归的方法quickSort,而非partition
*
* @param array
* @param left
* [left,right]
* @param right
* @return
*/
private int[] quickSort(int[] array, int left, int right) {
if (left >= right)// 递归的终止条件,这是必要的。
return array;
int pivotIndex = partition(array, left, right);// 初次分割
quickSort(array, left, pivotIndex - 1);// 快速排序基准数左边的数组
quickSort(array, pivotIndex + 1, right);// 快速排序基准数右边的数组
return array;
}
}
数组长度总共32, 执行交换次数:63
交换次数为中游表现。
时间复杂度为:
T(n) = O(n*log2^n)
-
最好情况:
快速排序使用了二分法,如果恰好每一次分割都正好将基准数摆在了中央位置,也就是恰好对半分,这时它的第二层嵌套次数为log2^N ,所以完整的时间复杂度为O(n*log2^n)。
-
最坏情况:
当每一次二分操作,有一侧只分到了一个元素,而另一侧是N-1个元素,那就是最坏的情况,即为第二层嵌套的次数仍为N,那么时间复杂度就是O(N^2)。
快速排序的空间复杂度很高,因为要二分分治,会占用log2^N 的临时空间去操作,同时还有快排的递归是与数组的长度相同,所以最终快速排序的空间复杂度为:
S(n) = O(n*log2^n)
切分要占用N个新的临时空间,排序比较又要占用log2^N ,所以完整的空间复杂度为O(n*log2^n)。
快速排序法就是集合了冒泡、二分分治和递归的思想。
堆排序
-
先来介绍堆的定义
这里的堆指的是数据结构中的“二叉堆”。二叉堆一般是通过数组来表示,每个元素都要保证大于等于另两个特定位置的元素。转化成二叉树的结构就是一个完全二叉树,若每个节点都小于等于它的父节点,这种结构就叫做“大顶堆”,也叫“最大堆”,而反过来,每个节点都大于等于它的父节点,这就是“小顶堆”,也叫“最小堆”。
-
再说一下堆的特性
在一个长度为N的堆中,位置k的节点的父节点的位置为k/2,它的两个子节点的位置分别为2k和2k+1,该堆总共有N/2个父节点。
-
修复堆有序的操作
当堆结构中出现了一个打破有序状态的节点,若它是因为变得比他的父节点大而打破,那么就要通过将其互换到更高的位置来修复堆,这个过程叫做由下而上的堆有序化,也叫 “上浮”。反过来,就是由上至下的堆有序化,也叫“下沉”。
-
堆排序的原理
堆排序是选择排序的延伸。根据堆的结构来看,就像一个三角形,根节点是唯一一层仅有一个数的节点,而同时它又必然是最大或者最小的一个。那么将该根节点取出来,然后修复堆,再取出修复后的根节点,以此类推,最终就会得到一个有序的数组。
-
堆排序的工作
堆排序总共分两步:
- 无序数组 -> 使堆有序
- 取出根节点 -> 使堆有序
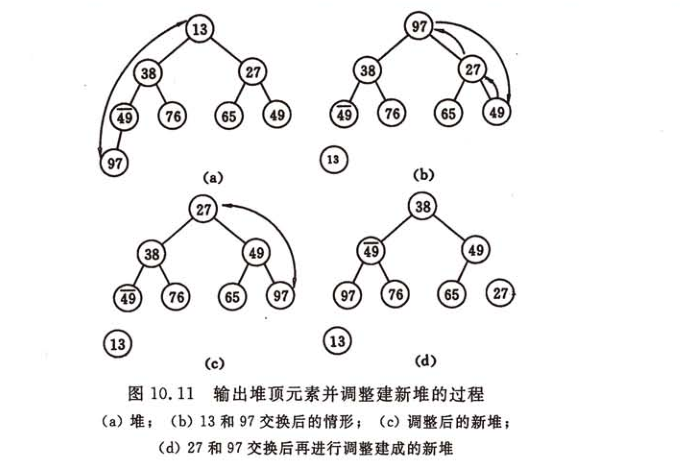
- 代码如下:
package algorithms.sort;
public class HeapSort extends Sort {
/**
* 下沉操作,让k的值array[k]下沉到合适位置,往下走就要跟子节点比较
* k位置的数值打破了大顶堆有序状态,说明其比子节点还小,这时就要将k与较大的子节点互换位置
* (不用考虑比父节点大的问题,因为循环到检查父节点的时候,依旧可以采用其比子节点小的逻辑)
* 7
* / \
* 6 3
* / \ / \
* 4 5 1 2
*
* @param array
* @param k
* 目标位置
* @param right
* 区间[k,right]
*/
private void sink(int[] array, int k, int right) {
// 循环终止条件1:左子并不存在,说明k目前已为叶节点,无处可沉
while (2 * k + 1 <= right) {
int bigChildIndex = 2 * k + 1;// left child index:2 * k + 1,right
// child index:2 * k + 2
// 如果有右子节点,且右子大于左子
if (2 * k + 2 <= right && array[2 * k + 1] < array[2 * k + 2])
bigChildIndex = 2 * k + 2;
if (array[k] > array[bigChildIndex])
// 循环终止条件2:k的值所处位置已堆有序,无处可沉,也就是说比他的子节点(一个或者两个子节点)都大
break;
swap(array, k, bigChildIndex);// 下沉,交换k和bigChildIndex
k = bigChildIndex;// 位置k已经换到了bigChildIndex
}
}
/**
* 上浮操作:让目标位置的值上浮到合适位置,往上走就要跟父节点比较
* k位置的数值打破了小顶堆有序状态,说明其比父节点还小,这时就要将k与其父节点互换位置
* (不用考虑比子节点大的问题,因为循环到检查子节点的时候,依旧可以采用其比父节点小的逻辑)
* 相对与下沉操作,上浮操作比较简略的原因是k只需要与一个父节点比较大小,而下沉操作则需要跟一个或两个子节点比较大小,多出的是这部分逻辑
* 1
* / \
* 2 5
* / \ / \
* 4 3 6 7
*
* @param array
* @param k
* 区间[0,k]
*/
private void swim(int[] array, int k) {
if (k == 0)
return;// k的位置已经是根节点了,不需要再上浮了。
// @@@@
// 终止条件:k不断往父节点一层层地爬或许能爬到根节点(k==0),或许中途k找到了比父节点大的位置,根据小顶堆规则,它就已经堆有序。
while (k > 0 && array[k] < array[(k - 1) / 2]) {// k的父节点:(k - 1) / 2
swap(array, k, (k - 1) / 2);// 上浮
k = (k - 1) / 2;// k换到了它的父节点的位置
}
}
/**
* 堆排序:下沉堆排序 注意:通过下沉操作可以得到大顶堆也可以得到小顶堆,这里只采用一种情况来介绍。
*
* @param array
* @return 从小到大排序
*/
private int[] sinkSort(int[] array) {
int maxIndex = array.length - 1;// 数组array,区间为 [0,maxIndex]
// 构造堆
int lastParentIndex = (maxIndex - 1) / 2;// 最后一个父节点位置
// @@@@如果使用下沉操作,一定要从最后一个父节点开始往根节点倒序检查,才能保证最大值被送到根节点@@@@
for (int i = lastParentIndex; i >= 0; i--) {// 区间[0,lastParentIndex]为当前数组的全部父节点所在
sink(array, i, maxIndex);// 区间[lastParentIndex,maxIndex],从最后一个父节点开始检查,下沉操作,调整堆有序
}
System.out.println("the max one is " + array[0]);
// 获得排序(注意:堆有序!=堆排序,堆有序只能保证根节点是最值,而不能保证子节点及树枝节点同级间的大小顺序)
while (maxIndex > 0) {
swap(array, 0, maxIndex--);// 取出最大值
sink(array, 0, maxIndex);// 修复堆
}
return array;
}
/**
* 堆有序:通过上浮操作,使堆有序
*
* @param array
* @param len
* 整理[0,len]区间的堆有序
*/
private void headAdjustBySwim(int[] array, int len) {
// @@@@如果使用上浮操作,一定要从最后一个叶节点开始,到根节点位置检查,才能保证最小值被送到根节点@@@@
for (int i = len; i > 0; i--) {// i不需要检查=0的情况,因为根节点没有父节点了。
swim(array, i);// 区间[0,i],从最后一个叶节点开始检查,上浮操作,调整堆有序
}
}
/**
* 堆排序:上浮堆排序 注意:通过上浮操作可以得到大顶堆也可以得到小顶堆,这里只采用一种情况来介绍。
*
* @param array
* @return 从大到小排序
*/
private int[] swimSort(int[] array) {
int maxIndex = array.length - 1;// 数组array,区间为 [0,maxIndex]
headAdjustBySwim(array, maxIndex);
System.out.println("the min one is " + array[0]);
// 获得排序(注意:堆有序!=堆排序,堆有序只能保证根节点是最值,而不能保证子节点及树枝节点同级间的大小顺序)
while (maxIndex > 0) {
swap(array, 0, maxIndex--);// 取出最小值
headAdjustBySwim(array, maxIndex);
}
return array;
}
@Override
protected int[] sort(int[] array) {
return swimSort(array);
}
}
上浮操作:数组长度:32,执行交换次数:185
下沉操作:数组长度:32,执行交换次数:139
通过结果可以看出,下沉操作的执行交换次数是较少的,因为下沉操作的目标位置只是所有的父节点,而上浮操作要遍历整个数组。所以,看上去,下沉操作效率会更高一些。
根据以上代码总结一下:
我们使用的数组举例如:{1, 12432, 47, 534, 6, 4576, 47, 56, 8}
-
将这些数组按原有顺序摆成完全二叉树的形式(注意二叉树,完全二叉树,满二叉树的定义,条件是逐渐苛刻的,完全二叉树必须每个节点都在满二叉树的轨迹上,而深度为N的满二叉树必须拥有2N-1个节点,不多不少。)
-
将该二叉树转换成二叉堆,最大堆或者最小堆均可
-
取出当前二叉树的根节点,然后用最后一个位置的元素来作为根节点,打破了二叉堆的有序状态。
-
堆有序修复
-
重复3.4步,直到数组取完全部元素为止
堆排序的时间复杂度为:
T(n) = O(n*log2^n)
空间复杂度也为O(1),原理同上。
-
注意:
下沉和上浮均可以处理无论是大顶堆还是小顶堆,他们并没有绑定关系。大顶堆时上浮可以是最后一个叶节点比父节点要大,所以上浮,下沉是最后一个父节点比子节点要小,所以下沉。小顶堆时就是反过来。另外,编写代码时要注意数组下标是从0开始,要细心处理一下。
希尔排序
希尔是个人,是希尔排序的发明者。
这是我觉得非常精巧的方案。
首先用图来表示一下希尔排序的中心思想:
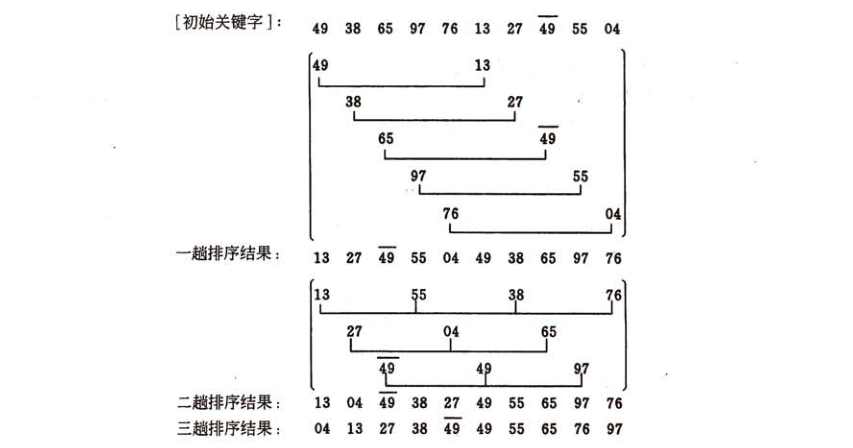
这张图可以清晰地展示希尔排序的思路。
具体代码如下:
package algorithms.sort;
public class ShellSort extends Sort {
@Override
protected int[] sort(int[] array) {
int lastStep = 0;// 控制循环次数,保存上一个step,避免重复
for (int d = 2; d < array.length; d++) {
int step = array.length / d;
if (lastStep != step) {
lastStep = step;
System.out.println("step: " + step);// 监控step,shellSort执行次数
shellSort(array, step);
} else {
continue;
}
}
return array;
}
private void shellSort(int[] array, int step) {
for (int i = 0; i < array.length - step; i++) {
if (array[i] < array[i + step]) {
swap(array, i, i + step);
}
}
}
}
数组长度:32,执行交换次数:56
希尔排序是精巧的,从交换次数上面来看表现也可以。
原理也是非常易懂,我很喜欢这种深入浅出的算法。
希尔排序的分析是复杂的,时间复杂度是所取增量的函数,这涉及一些数学上的难题。但是在大量实验的基础上推出当n在某个范围内时,时间复杂度可以达到O(n^1.3),,空间复杂度也为O(1),原理同上。
归并排序
归并排序的操作有些像快速排序,只不过归并排序每次都是强制从中间分割,递归分割至不可再分(即只有两个元素),将分割后的子数组进行排序,然后相邻的两个子数组进行合并,新建一个数组用来存储合并后的有序数组并重新赋值给原数组。
package algorithms.sort;
public class MergeSort extends Sort {
private int[] temp;
@Override
protected int[] sort(int[] array) {
temp = new int[array.length];// 新建一个与原数组长度相同的空的辅助数组
mergeSort(array, 0, array.length - 1);
return array;
}
/**
* 一到递归别迷糊:用于递归的方法MergeSort,而非merge
*
* @param array
* @param left
* @param right
*/
private void mergeSort(int[] array, int left, int right) {
if (left >= right)// 已经分治到最细化,说明排序已结束
return;
int mid = (right + left) / 2;// 手动安排那个两情相悦的位置,强制为中间。ㄟ(◑‿◐ )ㄏ
mergeSort(array, left, mid);// 左半部分递归分治
mergeSort(array, mid + 1, right);// 右半部分递归分治
merge(array, left, mid, right);// 强制安排两情相悦,就要付出代价:去插手merge他们的感情。( ͡°͜ʖ°)✧
}
/**
* 通过辅助数组,合并两个子数组为一个数组,并排序。
*
* @param array
* 原数组
* @param left
* 左子数组 [left, mid];
* @param mid
* 那个被强制的两情相悦的位置。(ಠ .̫.̫ ಠ)
* @param right
* 右子数组 [mid+1, right]
*/
private void merge(int[] array, int left, int mid, int right) {
for (int k = left; k <= right; k++) {// 将区间[left,right]复制到temp数组中,这是强硬合并,并没有温柔的捋顺。
temp[k] = array[k];
}
int i = left;
int j = mid + 1;
for (int k = left; k <= right; k++) {// 通过判断,将辅助数组temp中的值按照大小归并回原数组array
if (i > mid)// 第三步:亲戚要和蔼,左半边用尽,则取右半边元素
array[k] = temp[j++];// 右侧元素取出一个以后,要移动指针到其右侧下一个元素了。
else if (j > right)// 第四步:与第三步同步,工作要顺利,右半边用尽,则取左半边元素
array[k] = temp[i++];// 同样的,左侧元素取出一个以后,要移动指针到其右侧下一个元素了。
else if (array[j] > temp[i])// 第一步:性格要和谐,右半边当前元素大于左半边当前元素,取右半边元素(从大到小排序)
array[k] = temp[j++];// 右侧元素取出一个以后,要移动指针到其右侧下一个元素了。
else// 第二步:与第一步同步,三观要一致,左半边当前元素大于右半边当前元素,取左半边元素(从大到小排序)
array[k] = temp[i++];// 同样的,左侧元素取出一个以后,要移动指针到其右侧下一个元素了。
}
}
}
数组长度:32,执行交换次数:0
由于全程代码中并没有涉及交换操作,所以交换次数为0。
归并排序的空间复杂度很高,因为它建立了一个与原数组同样长度的辅助数组,同时要对原数组进行二分分治,所以空间复杂度为
S(n) = O(n*log2^n)
时间复杂度比较低,与空间复杂度的计算方式差不多,也为O(n*log2^n) 。
归并排序是一种渐进最优的基于比较排序的算法。但是它的空间复杂度很高,同时也是不稳定的,当遇到最坏情况,也即每次比较都发生数据移动时,效率也不高。
计数排序
直接上代码,注释里面说:
package sort;
public class CountingSort extends Sort {
@Override
protected int[] sort(int[] array) {
countingSort(array);
return array;
}
/*
* 计数排序
*
* @example [1,0,2,0,3,1,1,2,8] 最大值是8,建立一个计数数组a[]统计原数组中每个元素出现的次数,长度为9(因为是从0到8)
*
* @开始计数:第一个统计0的次数为2,则a[0]=2;第二个统计1的次数为3,则a[1]=3;第三个按照数组下标以此类推,最终获得一个统计数组。
*
* @开始排序:因为按照统计数组的下标,已经是有顺序的,只要循环输出每个重复的数就可以了。
*/
private void countingSort(int[] array) {
int max = max(array);
// 开始计数
int[] count = new int[max + 1];
for (int a : array) {
count[a]++;
}
// 输出回原数组
int k = 0;
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
array[k++] = i;
}
}
}
}
数组长度总共32, 执行交换次数:0
这个计数排序算法也挺巧妙,他巧妙地应用了数组下标本身的顺序性,将下标当做参照物去比对原数组,把与下标相同的数字出现的次数记录到该下标的值中。
然后再遍历计数数组,按次数循环输出数字到原数组,即可得到一个有序数组。
时间复杂度
T(n) = O(n)
计数排序算法的最大优势,是他的时间复杂度很小,远小于其他基于比较的排序算法。
下面说一下这个时间复杂度是如何计算出来的,整段代码中只有一个嵌套循环,其他的都是一层循环,也就是O(n)。观察这个两层的循环可以发现,如果count数组长度为1,只有一个数字,但是原数组长度为100,那么这个两层循环只是遍历100次,仍旧是O(n),而如果count数组长度为100,里面并没有重复的数字出现,那么第二层循环只循环一次,仍旧是O(n),从这两头的极端情况可以发现,这个两层嵌套很好理解,无论原数组是什么结构,他的时间复杂度不会变,仍旧是O(n)。
空间复杂度
S(n) = O(X)
而计数排序的空间复杂度则较高,因为他有一个辅助数组count,这个数组会根据原数组内部元素的重复情况开辟新的内存空间。辅助数组的大小完全取决于原数组的最大值,最大值如果非常大的话,辅助数组也就变得非常长,那空间复杂度会很高,原数组的最大值并不大,那么空间复杂度就不高。而原数组的最大值是无法通过长度N来衡量的,所以计数排序的空间复杂度无法给出。
桶排序
桶排序是一种高级排序算法,是比以上各种的更优化的一种排序算法。基于比较的排序算法的时间复杂度的下限是O(n*log2^n ),不会比这个更小了。但是确实存在更快的算法,这些算法不是不使用比较,而是使用某些限定条件,让参与比较的操作尽可量减小。桶排序是这样的,它的原理与计数排序很像,但更复杂。
桶排序的基本思想:建立一个辅助桶序列,通过某种限定关系,它是一种映射函数f(n)将原数组的元素分配到辅助桶中,每个辅助桶可以存一个数组,最终这个桶序列会按照f(n)把原数组的元素全部存入进来。然后针对每个桶内部的数组进行比较排序,可以选择以上属于比较排序中的任一种,这里我们选择使用快速排序。最后,把辅助桶序列内的元素按顺序输出到原数组内即可。
用上面的计数算法来解释:就是那个辅助数组的每个下标不再存储单个数字的重复次数了,而是在存按照f(n)分配后的大于0个的元素,通俗来讲,就是计数算法中的辅助数组的每个下标现在开始存数组了,这个下标现在就是一个桶,是一个数组,计数排序中的辅助数组现在是一个数组序列,多个数组的集合。
桶排序准备:
1.我们需要一个辅助数组集合。因为数组必须先指定长度,所以这里用自适应大小的List<Integer>来存储数组的元素,作为一个桶,桶集合为List<List<Integer>>
2.一个映射函数f(n)
代码如下:
package sort;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class BucketSort extends Sort {
private List<List<Integer>> buckets = new ArrayList<List<Integer>>();
private int optimizeDivisor = 0;
private int bucketNum = 100;// 这个桶个数要提前定义
private int divisor = 1;
private int f(int n) {
return n / divisor;
}
@Override
protected int[] sort(int[] array) {
bucketSort(array);
System.out.println("divisor=" + divisor + ", 桶排序优化程度:" + optimizeDivisor);
return array;
}
private void bucketSort(int[] arr) {
divisor = max(arr) / bucketNum + 1;
for (int i = 0; i < bucketNum; i++) {
buckets.add(new LinkedList<Integer>());
}
for (int a : arr) {
buckets.get(f(a)).add(a);
}
int k = arr.length - 1;
for (int i = 0; i < bucketNum; i++) {
if (!buckets.get(i).isEmpty()) {
optimizeDivisor++;
List<Integer> list = buckets.get(i);
int[] bucket = new int[list.size()];
for (int j = 0; j < list.size(); j++) {
bucket[j] = list.get(j);
}
Sort quickSort = new QuickSort();
bucket = quickSort.sort(bucket);// 如果是从小到大排序,那就正序插入,反之从大到小则倒序插入
for (int j = bucket.length - 1; j >= 0; j--) {
arr[k--] = bucket[j];
}
}
}
}
}
divisor=1, 桶排序优化程度:29(这个值越大越好,越大说明快排参与的越少)
数组长度总共32, 执行交换次数:0
从代码中可以看出,桶排序是上面其他的比较排序的一个优化算法。但是桶的数量要根据原数组的取值范围去提前计算好,因为桶的数量越多,原数组的值越能平均分配到每个桶中去,相应的快速排序参与的部分就越少,时间复杂度就越低,但是空间复杂度就会越高,这是一个空间换时间的权衡。
桶的数量和每个桶的区间最好是能够隔离开原数组出现频率非常高的元素们,最大个数不要超过原数组最大元素的值,因为超过了将会有很多空桶,我们追求每个桶内元素尽量少的同时,又要追求整个桶集合中空桶数量尽量少。
所以使用桶排序要把握好桶个数和f(n)映射函数,将会大大提高效率。这很纠结,I know.<(▰˘◡˘▰)>
时间复杂度,最优情况就是每个桶都最多有一个元素,那么就完全不需要比较排序了,时间复杂度为O(n)。最坏情况就是只有一个桶拥有了所有原数组的元素,然后这个桶要完全使用比较排序去做,那么再赶上原数组的数值情况在那个比较排序算法里也是最坏情况,那时间复杂度可以达到O(n^2)
空间复杂度就不要说了,桶排序就是一个牺牲空间复杂度的算法。
基数排序
基数排序的中心思想:每次只比较原数组元素的一位数,将顺序记录下来,然后再比较下一位数,逐渐让数组有序起来,比较的位数是从小到大的。
如图所示:
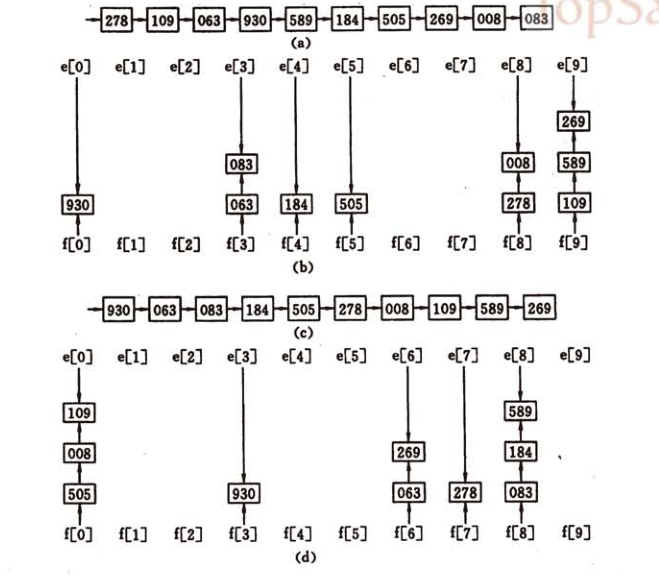
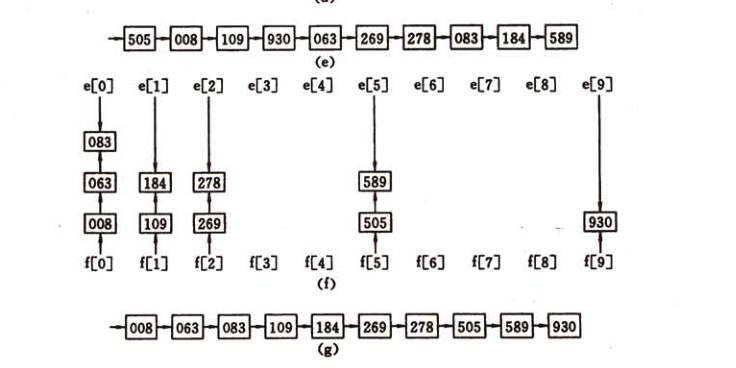
准备工作:
- 我们需要一个集合,因为是动态大小,仍旧采用 List<List<Integer>>
- 需要一个可以获得某数字的某一位数的方法
- 要获得该数组的最大位数
- 分配方法:将数组中的元素按照某一位数的拆分分配到集合中去
- 收集方法:将集合中的元素按顺序传回数组
代码如下:
package sort;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class RadixSort extends Sort {
@Override
protected int[] sort(int[] array) {
return radixSort(array);
}
private int[] radixSort(int[] arr) {
int maxBit = String.valueOf(max(arr)).length();// 获得最大位数
for (int i = 1; i <= maxBit; i++) {// 最大位数决定再分配收集的次数
List<List<Integer>> list = new ArrayList<List<Integer>>();
// list 初始化,位数的值无外乎[0,9],因此长度为10
for (int n = 0; n < 10; n++) {
list.add(new LinkedList<Integer>());
}
// 分配
for (int a : arr) {
list.get(getBitValue(a, i)).add(a);// 将原数组的元素的位数的值作为下标,整个元素的值作为下标的值
}
// 收集
int k = 0;
for (int j = 0; j < list.size(); j++) {
if (!list.get(j).isEmpty()) {// 加一层判断,如果list的某个元素不为空,再进入下面的元素内部循环
for (int a : list.get(j)) {
arr[k++] = a;
}
}
}
}
return arr;
}
/**
* 获得某数字的某一个位的值,例如543的十位数为4
*
* @param target
* 待处理数字
* @param BitNum
* 从右向左第几位数,例如142512,BitNum为3的话,对应的值为5
* @return
*/
private int getBitValue(int target, int BitNum) {
String t = String.format("%" + BitNum + "d", target).replace(" ", "0");// 如果位数不够,则用0补位
return Integer.valueOf(String.valueOf(t.charAt(t.length() - BitNum)));
}
}
数组长度总共32, 执行交换次数:0
这是一个按照最大位数不断分配收集的过程,并不基于比较,也不是交换,如同上面的计数排序,分配时也是将位数的值作为下标,只是不再存储元素重复出现的次数,而是存储该位数相同的值们,有些绕,可以结合基数排序与计数排序的代码慢慢理解。
举例说明:数组在第一次分配收集以后,元素按照个位数的大小被划分出来,再经历第二次分配收集以后,元素在上一次数组的处理结果之上继续按照十位数的大小被划分出来,以此类推,最终,会按照元素进入数组的顺序获得一个有序数组。
时间复杂度:基数排序的时间复杂度计算比较复杂,我们通过代码进行分析,首先是按照最大位数进行循环,这个最大位数很难去定义,它不是数组的长度N,而是要找出最大值然后判断最大值的位数,这是与N无关的,例如数组{1,100001},N为2,但是最大位数为6,这个在时间复杂度中很难表现,就记录为O(X)吧。接着又嵌套了一层,这一层中有三个循环,第一个循环是确定次数的,就是10次,因为是从0到9,确定的;第二个循环是按照数组的长度N,所以这里是O(N);第三个循环是按照集合的大小循环,其实也是数组的长度,仍为O(n)。所以如果N>10,在问题规模的增大下,可以忽略那个10次的循环,时间复杂度就是
T(n) = O(n*X)
如果N<10的话,时间复杂度就是
T(n) = O(10*X)
空间复杂度:这些基于非比较的排序都是比较消耗空间的,因为都需要一个辅助集合,这个集合占用的空间与原数组一致。所以是
S(n) = O(n)
总结
以上十种排序算法介绍完毕,下面对于他们的思路进行一个归纳,如下图所示:
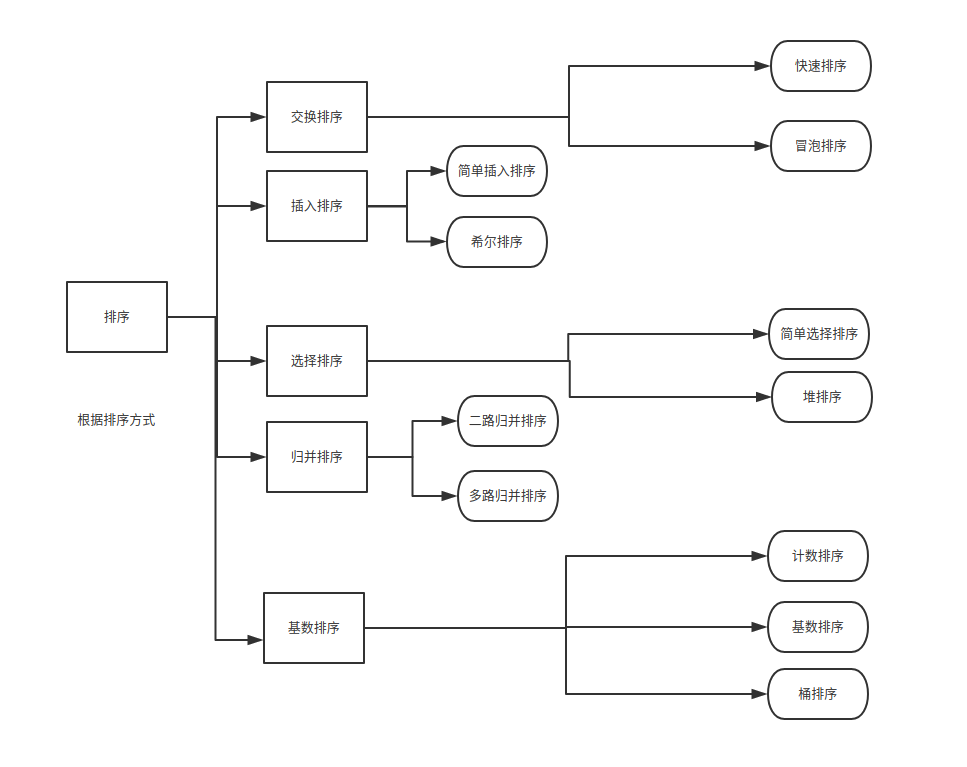
选择排序:
交换:
冒泡排序和快速排序都是基于比较+交换的;
选择排序和堆排序都是基于选择+交换的;
插入排序和希尔排序都是基于比较+插入的;
归并排序是基于比较+合并
非选择排序:
桶排序、计数排序、基数排序
在我们的日常编程之中,很多程序设计语言已经内置了排序方法供我们直接调用,但我们也会遇到亲自去使用他们的时候,平时我们使用的快速排序的概率比较大,这并不代表其他排序算法就是无用的,基于不同的数值情况,选择不同的排序算法,达到最优的效率,帮助整个系统更加高效的运转,这是算法给我们带来的,不是纯靠堆积硬件配置换来的效率,而是靠知识。。。知识是第一生产力 (๑˘ ˘๑) ,而如果你是一名算法工程师,恐怕这些算法你要研究的比程序员要透彻很多,甚至要研究更复杂更适用于你们业务情况的排序算法。在研究这些里程碑的算法时,我们能够发现他们的作者都有着非常创造性的思维,想方设法去寻找更加高效的排序算法,这些大师的作品将被记录成经典,永远在程序员界流传着他们的思想。
文章所有源码位置
参考资料
- 《数据结构》严蔚敏 吴伟民 编著
- 《算法 第四版》
- 网上大牛们的帖子,以及他们的图 (●'◡'●)ノ♥



