数据压缩的元老——哈夫曼树精解
数据结构从逻辑结构上可以分为:集合、线性表、树、图
集合中常用的数据结构是背包等。
线性表包括栈、链表、队列等。
树包括堆、二叉树、哈夫曼树等。
图包括有向图、无向图、最小生成树、最短路径等(就职于高德地图的算法工程师,图的知识必须完全掌握(ง •̀_•́)ง)。
-
背包、栈、链表和队列在之前的一篇博文《基础大扫荡——背包,栈,队列,链表一口气全弄懂》中介绍了一下。二叉树和堆在《面向程序员编程——精研排序算法》中的堆排序部分仔细介绍过。
图若在未来有机会用到我会去研究一下,目前为止我的经历中用到图结构的不多。 -
数据结构从存储结构(也就是物理结构)上可以分为:顺序、链接、索引、散列。这一部分我将会新开一篇博文《精研查找算法》中进行详细分析。(TODO: 挖坑于此)
-
数据结构和算法这一主题我最想做的是排序和查找,然而在此过程中,重温了数据结构的一些知识,发现了哈夫曼树,大学时期,我的数据结构分数很一般(当时心思并没有放在学习上,对不起李晓明老师),但当时对哈夫曼树也有所了解。今天重新认识了它,感觉它是很精妙的算法,也是现代计算机数据压缩的始祖。
下面我们分别从数据压缩的简介,数据(位、字节、字符)的简介,到哈夫曼树,哈夫曼编码来详细分析。
数据压缩
现代IT产业经常提及“大数据”,实际上伴随着计算机行业兴起,数据就占据着最重要的地位,近年来,数据的增长量也是越来越大。
数据压缩可以节省数据存储的空间,以及节省数据传输的时间,在如此巨大的数据量面前,效果显著。
-
数据压缩的原理简介:
图像、电影、音乐,数据不仅仅限制于文本,绝大多数数据会有冗余,例如在文本文件中,很多字符出现的频率远高于其他字符,图片编码中也存在大片的相同区域,电影、声音等类似信号的文件都含有大量重复模式。
将这些重复的区域进行压缩处理,整个文件所占的存储空间将会大大减小。 -
数据压缩的性能指标:就是压缩时间,以及算法的压缩率(比起源文件缩小存储空间的比率)。
-
分类:有损压缩算法,无损压缩算法。我们常听到的“无损音乐”就是通过无损压缩的,无损压缩可以保证不丢失任何信息,解压以后的文件与源文件完全相同,哈夫曼编码就是常见的无损压缩算法。而实际上我们听的大部分音乐的码率是320kbit/s,192kbit/s,128kbit/s,他们都属于有损压缩。随着码率的减小,每秒传输的数据量越来越少,你听到的内容就没那么丰富,音质也就会越来越低,但是压缩率越来越高,文件大小越来越小,网络传输的时候也就越顺畅。
一个简单的例子
计算机内部数据类型最小单元为bit,也叫位、比特。但是一般编程语言处理的最小单位为byte,也叫字节、8位元组。通过定义也能知道,1个byte等于8个bit。Java 中,8位的char编码为1个字节,16位的short编码为2个字节,32位的int编码为4个字节。
《爸爸去哪儿5》10月底一期,山上展示了一串数字是“52088”,现在要把这些数字存进来。下面展示几种方式:
- 直接存入int a = 52088,这将占据32位的空间。
- short a = 52088,这将占据16位的空间。比short再小的单位不能存储52088了,因为short的边界就是65536-1=65535。char的边界是256-1=255。
- 将520和88分开存储,short=520,char=88,将占据16+8=24位的空间。
- 不用Java的数据类型,直接用位输出,520需要10位,88需要7位,总共占17位。
- 直接用位输出,进一步拆分源数据,5,2,0,8,8,分别用位存入,就是3位+2位+1位+4位+4位=14位。
最终第五种方式占用空间最小,这是最粗糙的一种数据压缩的方式。
二进制转储
我们知道计算机中所有类型的数据最终都是用二进制(0和1,计算机用高电平和低电平分别表示0和1)表示。网络传输过程中,数据往往是通过比特流或者字节流的方式在网络中通信。比特流就是我们熟知的种子下载,p2p,免费、自由。字节流就是我们传统并常见的数据传输方式。程序员在调试过程中,是如何查看比特流和字节流的呢?我们如果直接打开一个二进制文件,看到的将是一团乱码,乱码的内容随着你操作系统的不同而不同,转储(dump)就是将这些乱码转换成我们看得懂的方式。例如可以转为二进制,以0和1表示,也可以转为8位的字节,甚至可以转为图片文件,0为白色像素,1为黑色像素。前两天我们公司系统出bug,就是采用的TCP dump的工具进行调试,很快发现了网络通信中的问题根源。代码中,我们一般会用管道方式将二进制文件传给这些dump编解码工具,或者直接重定向到另一个文件。
ASCII编码
单字节编码系统,世界上语言众多,直接拿比特数据给别人看,谁也看不懂,因此诞生了单字节编码对照系统,它规定了哪些二进制数代表哪些字符。第一版的ASCII编码采用7位二进制数共计代表了128个字符,包括数字0-9,大小写字母a-z、A-Z,以及标点符号、运算符号和一些控制命令符号。英语用这128个字符就够了,但是其他语言不行,后来在它的基础上增加一位,也就是8位,可表示256个字符,前128个字符仍旧与第一版保持一致,而后128个字符被称作“扩展字符编码”,扩展字符集,每个地区国家都有自己的一个版本,所以无法达到世界通用的目的。这就造成了很大问题,当你拿到一个文件,如果不按照当初的编码打开,就会得到一堆乱码。这时出现了Unicode编码,它将全世界所有的字符编码集合到了一起。Unicode也有问题,因为某些语言或者符号要用大于一个字节来表示,这就与基础的ASCII出现了冲突,计算机如何知道这一个字节是代表ASCII中的字符还是Unicode中某个字符的一部分呢?随着互联网出现,UTF系列编码出现了,当前最流行的就是UTF-8编码格式,它加长了编码,设立了标志位,可以有效区分出英语和其他语言的字符。
数据压缩的局限
- 不存在能够压缩任意比特流的算法,否则递归调用,原比特流最终会被压缩为0,这显然是荒谬的。
- 不可判定性,由于压缩算法的压缩率非常依赖源数据本身的格式,因此对于源数据的众多情况,我们找不到最佳的压缩算法。
哈夫曼树
带权路径长度最小的二叉树叫哈夫曼树。
- 权:权重,比重,是当前结点所占整体的百分比。
- 树的路径长度:从该二叉树的每一个结点到根结点的路径长度之和。
- 路径长度:一个结点到另一个结点之间的边有几个。
- 带权路径长度:WPL(Weight Path Length),结点的权与路径长度的乘积。
如图:
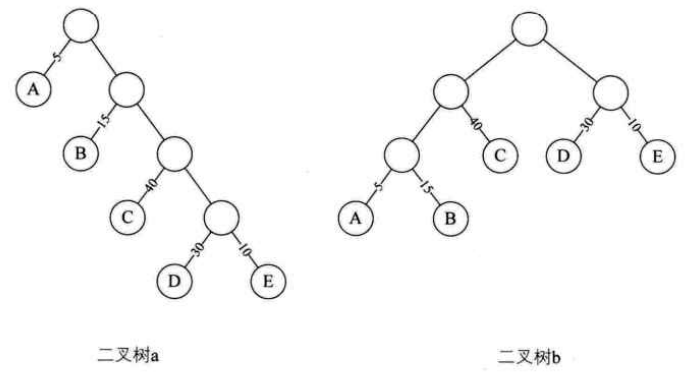
A占5%,B为15%,C为40%,D为30%,E为10%。对应的每个结点的权就是他们所占的百分比。
二叉树a的WPL值为:1*5+2*15+3*40+4*30+4*10=315
二叉树b的WPL值为:3*5+15*3+40*2+30*2+10*2=220
由此可见,二叉树b的带权路径长度要小于二叉树a,我们的目的就是让权值大的结点尽量路径长度小一些,这样可以保证总效率提高。
哈夫曼树的构建:
- 按照权值大小排序,A5,E10,B15,D30,C40。
- 取前两位当做子结点,新建辅助结点N1作为其父结点。
- 让第三位与N1做兄弟结点,此时N1节点的权为其两个子节点的权之和15,注意相对较小的弟弟结点要放在左边,新建辅助结点N2作为其父结点。
- 重复第3步,直到将所有结点都归纳到树中。
如图:
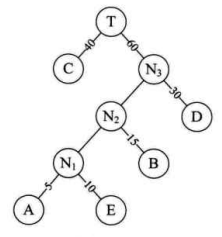
此时该二叉树的WPL值为:4*5+10*4+15*3+30*2+40*1=205
该二叉树的WPL值比上面的二叉树b还少了15,此时构建的二叉树才是WPL最小的,才是标准的哈夫曼树,也叫最优二叉树。
哈夫曼编码
接着使用上面的例子,我们按照他们的权值要传输1个A,2个E,3个B,6个D,8个C。连起来就是:
AEEBBBDDDDDDCCCCCCCC
共20个字符,按约定转为二进制数:
| A | B | C | D | E |
|---|---|---|---|---|
| 000 | 001 | 010 | 011 | 100 |
取数据的时候仍旧按照这个约定再将他们取出即可。
那么存储时就是一串二进制数:
000100100001001001011011011011011010010010010010010010010
三位一组表示一个字母,共60个数。
现在我们要使用哈夫曼编码,利用上面已经构建出来的哈夫曼树,将所有左子路径的权都改为0,右子的权都改为1,如图:
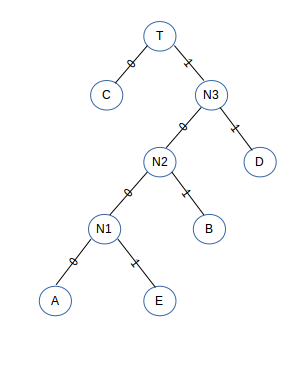
从根节点开始拼凑,我们用这些0和1来编码,得出结果为:
| A | B | C | D | E |
|---|---|---|---|---|
| 1000 | 101 | 0 | 11 | 1001 |
那么,现在的二进制数串为:
10001001100110110110111111111111100000000
共40个数。
也就是说我们的数据被压缩到67%,节约了33%的空间,随着原字符的增加和权重的变化,这种压缩效率会更高。
解码
以上就是哈夫曼编码的内容,那么我们该如何解码呢?
在上面第一种原始的方式中,我们可以直接按照三位一截取,然后对比我们的约定表格,还原源字符串。然而我们利用哈夫曼编码以后,发现每个字符换成的二进制数的长度不同了,二进制数中非0即1,如果长度不同,很容易混淆。
若要设计长短不等的编码,则必须任意字符的编码都不是另一字符的前缀,这种编码称作前缀编码。
我们仔细观察编码后的二进制串,发现按照约定表格,从第一个字符1000换成A以后,第二个是1001,换成E,后面的并没有出错。
注意
-
构建哈夫曼树时,左子一定是较小的弟弟结点。
-
哈夫曼编码时,权改为0和1,一定是要约定好顺序,是从根到结点还是到结点到根,约定好以后,所有结点均按照此顺序执行。
参考资料
- 《大话数据结构》程杰著
- 《算法第4版》



