caffe源码 全连接层

图示全连接层

 

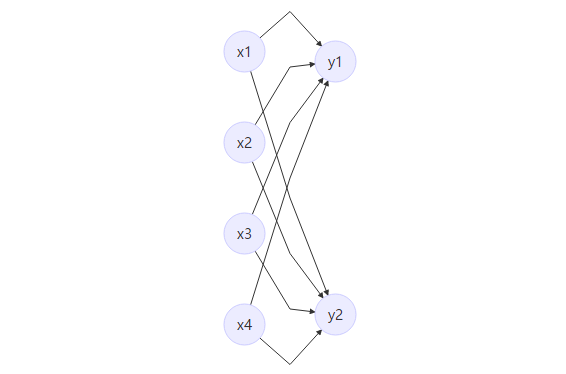
• 如上图所示，该全链接层输入n * 4，输出为n * 2，n为batch
• 该层有两个参数W和B，W为系数，B为偏置项
• 该层的函数为F(x) = W*x + B，则W为4 * 2的矩阵，B 为 1 * 2 的矩阵

从公式理解全连接层

假设第N层为全连接层，输入为Xn，输出为Xn+1，其他与该层无关的信息可以忽略

• 该层公式有Xn+1 = Fn(Xn) = W * Xn + B

前向传播

• 已知Xn，Xn+1 = W * Xn + B， 为前向传播

反向传播

反响传播这里需要求两个梯度，loss 对 W的梯度 和 loss 对 B 的梯度，

• loss 对 W 的梯度
  • 具体公式如下：
• loss 对 B 的梯度
  • 具体公式如下：
• 上面两个梯度都用到了loss 对 该层输出的梯度，所以在这层应该把loss 对该层输入的梯度传递到上一层。
  • 具体公式如下：

caffe中innerproduct的代码

前向传播

这一步在代码里面分为两步：

• Xn+1 = W * Xn，如下图：
  • 
• Xn+1 = Xn+1 + B，如下图：
  • 
• 和上面推导的一样

反向传播

这里需要求三个梯度，loss 对 W的梯度 ，loss 对 B的梯度， loss 对 Xn的梯度

• loss 对 W 的梯度
  • 公式：
  • 代码： 
  • 以上公式和推导的公式有点区别，后面加多loss 对W 的梯度，实现的是累积梯度
• loss 对 B 的梯度
  • 公式：
  • 代码：
  • 以上公式和推导的公式有点区别，后面加多loss 对B 的梯度，实现的是累积梯度
• loss 对 Xn 的梯度,：
  • 公式： 
  • 代码：
  • 公式和推导的并无区别