容斥原理

对容斥原理的描述

容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。

描述

容斥原理可以描述如下：

要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

关于集合的原理公式

上述描述的公式形式可以表示如下：

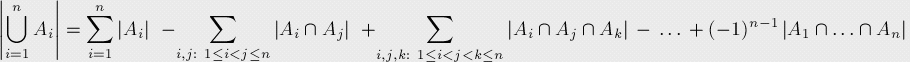
它可以写得更简洁一些，我们将B作为所有Ai的集合，那么容斥原理就变成了：

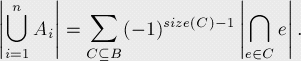
这个公式是由 De Moivre (Abraham de Moivre)提出的。

关于维恩图的原理

用维恩图来表示集合A、B和C：

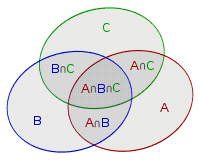
那么的面积就是集合A、B、C各自面积之和减去 , , 的面积，再加上的面积。

由此，我们也可以解决n个集合求并的问题。

关于概率论的原理

设事件，代表发生某些事件的概率（即发生其中至少一个事件的概率），则：

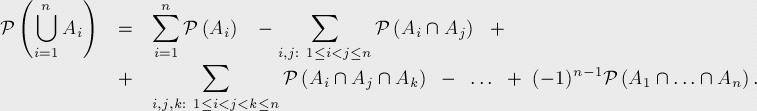
这个公式也可以用B代表Ai的集合：

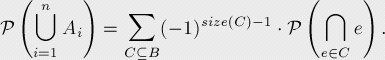
容斥原理的证明

我们要证明下面的等式：

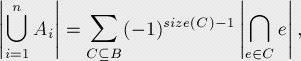
其中B代表全部Ai的集合

我们需要证明在Ai集合中的任意元素，都由右边的算式被正好加上了一次（注意如果是不在Ai集合中的元素，是不会出现在右边的算式中的）。

假设有一任意元素在k个Ai集合中（k>=1），我们来验证这个元素正好被加了一次：

当size(C)=1时，元素x被加了k次。

当size(C)=2时，元素x被减了C(2,k)次，因为在k个集合中选择2个，其中都包含x。

当size(C)=3时，元素x被加了C(3,k)次。

……

当size(C)=k时，元素x被加/减了C(k,k)次，符号由sign(-1)^(k-1)决定。

当size(C)>k时，元素x不被考虑。

然后我们来计算所有组合数的和。

由二项式定理，我们可以将它变成：

我们把x取为1，这时表示1-T（其中T为x被加的总次数），所以，证明完毕。

对于实际问题的应用

容斥原理的理论需要通过例子才能很好的理解。

首先，我们用三个简单的例子来阐释这个理论。然后会讨论一些复杂问题，试看如何用容斥原理来解决它们。

其中的“寻找路径数”是一个特殊的例子，它反映了容斥问题有时可以在多项式级复杂度内解决，不一定需要指数级。

一个简单的排列问题

由0到9的数字组成排列，要求第一个数大于1，最后一个数小于8，一共有多少种排列？

我们可以来计算它的逆问题，即第一个元素<=1或者最后一个元素>=8的情况。

我们设第一个元素<=1时有X组排列，最后一个元素>=8时有Y组排列。那么通过容斥原理来解决就可以写成：

经过简单的组合运算，我们得到了结果：

然后被总的排列数10!减，就是最终的答案了。

（0,1,2）序列问题

长度为n的由数字0，1，2组成的序列，要求每个数字至少出现1次，这样的序列有多少种？

同样的，我们转向它的逆问题。也就是不出现这些数字的序列不出现其中某些数字的序列。

我们定义Ai(i=0…2)表示不出现数字i的序列数，那么由容斥原理，我们得到该逆问题的结果为：

可以发现每个Ai的值都为2^n（因为这些序列中只能包含两种数字）。而所有的两两组合都为1（它们只包含1种数字）。最后，三个集合的交集为0。（因为它不包含数字，所以不存在）

要记得我们解决的是它的逆问题，所以要用总数减掉，得到最终结果：

方程整数解问题

给出一个方程：

其中。

求这个方程的整数解有多少组。

我们先不去理会xi<=8的条件，来考虑所有正整数解的情况。这个很容易用组合数来求解，我们要把20个元素分成6组，也就是添加5块“夹板”，然后在25个位置中找5块“夹板”的位置。

然后通过容斥原理来讨论它的逆问题，也就是x>=9时的解。

我们定义Ak为xk>=9并且其他xi>=0时的集合，同样我们用上面的添加“夹板”法来计算Ak的大小，因为有9个位置已经被xk所利用了，所以：

然后计算两个这样的集合Ak、Ap的交集：

因为所有x的和不能超过20，所以三个或三个以上这样的集合时是不能同时出现的，它们的交集都为0。最后我们用总数剪掉用容斥原理所求逆问题的答案，就得到了最终结果：

求指定区间内与n互素的数的个数：

给出整数n和r。求区间[1;r]中与n互素的数的个数。

去解决它的逆问题，求不与n互素的数的个数。

考虑n的所有素因子pi(i=1…k)

在[1;r]中有多少数能被pi整除呢？它就是：

然而，如果我们单纯将所有结果相加，会得到错误答案。有些数可能被统计多次（被好几个素因子整除）。所以，我们要运用容斥原理来解决。

我们可以用2^k的算法求出所有的pi组合，然后计算每种组合的pi乘积，通过容斥原理来对结果进行加减处理。

关于此问题的最终实现：

 1 int solve (int n, int r) {
 2         vector<int> p;
 3         for (int i=2; i*i<=n; ++i)
 4                if (n % i == 0) {
 5                        p.push_back (i);
 6                        while (n % i == 0)
 7                                n /= i;
 8                }
 9         if (n > 1)
10                p.push_back (n);
11         int sum = 0;
12         for (int msk=1; msk<(1<<p.size()); ++msk) {
13                int mult = 1,
14                        bits = 0;
15                for (int i=0; i<(int)p.size(); ++i)
16                        if (msk & (1<<i)) {
17                                ++bits;
18                                mult *= p[i];
19                        }
20                int cur = r / mult;
21                if (bits % 2 == 1)
22                        sum += cur;
23                else
24                        sum -= cur;
25         }
26         return r - sum;
27 
28 }

算法的复杂度为。

求在给定区间内，能被给定集合至少一个数整除的数个数

给出n个整数ai和整数r。求在区间[1;r]中，至少能被一个ai整除的数有多少。

解决此题的思路和上题差不多，计算ai所能组成的各种集合（这里将集合中ai的最小公倍数作为除数）在区间中满足的数的个数，然后利用容斥原理实现加减。

此题中实现所有集合的枚举，需要2^n的复杂度，求解lcm需要O(nlogr)的复杂度。

能满足一定数目匹配的字符串的个数问题

给出n个匹配串，它们长度相同，其中有一些’?’表示待匹配的字母。然后给出一个整数k，求能正好匹配k个匹配串的字符串的个数。更进一步，求至少匹配k个匹配串的字符串的个数。

首先我们会发现，我们很容易找到能匹配所有匹配串的字符串。只需要对比所有匹配串，去在每一列中找出现的字母（或者这一列全是’?’，或者这一列出现了唯一的字母，否则这样的字符串就存在），最后所有字母组成的单词即为所求。

现在我们来学习如何解决第一个问题：能正好匹配k个匹配串的字符串。

我们在n个匹配串中选出k个，作为集合X，统计满足集合X中匹配的字符串数。求解这个问题时应用容斥原理，对X的所有超集进行运算，得到每个X集合的结果：

此处f(Y)代表满足匹配集合Y的字符串数。

如果我们将所有的ans(X)相加，就可以得到最终结果：

这样，就得到了一个复杂度的解法。

这个算法可以作一些改进，因为在求解ans(X)时有些Y集合是重复的。

回到利用容斥原理公式可以发现，当选定一个Y时，所有中X的结果都是相同的，其符号都为。所以可以用如下公式求解：

这样就得到了一个复杂度的解法。

现在我们来求解第二个问题：能满足至少k个匹配的字符串有多少个。

显然的，我们可以用问题一的方法来计算满足k到n的所有结果。问题一的结论依然成立，不同之处在于这个问题中的X不是大小都为k的，而是>=k的所有集合。

如此进行计算，最后将f(Y)作为另一个因子：将所有的ans做和，有点类似二项式展开：

在《具体数学》( Graham, Knuth, Patashnik. "Concrete Mathematics" [1998] )中，介绍了一个著名的关于二项式系数的公式：

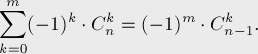
根据这个公式，可以将前面的结果进行化简：

那么，对于这个问题，我们也得到了一个的解法：

路径的数目问题

在一个的方格阵中，有k个格子是不可穿越的墙。一开始在格子(1,1)（最左下角的格子）中有一个机器人。这个机器人只能向上或向右行进，最后它将到达位于格子(n,m)的笼子里，其间不能经过障碍物格子。求一共有多少种路线可以到达终点。

为了方便区分所有障碍物格子，我们建立坐标系，用(x,y)表示格子的坐标。

首先我们考虑没有障碍物的时候：也就是如何求从一个点到另一个点的路径数。如果从一个点在一个方向要走x个格子，在另一个方向要走y个格子，那么通过简单的组合原理可以得知结果为：

现在来考虑有障碍物时的情况，我们可以利用容斥原理：求出至少经过一个障碍物时的路径数。

对于这个例子，你可以枚举所有障碍物的子集，作为需要要经过的，计算经过该集合障碍物的路径数（求从原点到第一个障碍物的路径数、第一个障碍物到第二个障碍物的路径数…最后对这些路径数求乘积），然后通过容斥原理，对这些结果作加法或减法。

然而，它是一个非多项式的解法，复杂度。下面我们将介绍一个多项式的解法。

我们运用动态规划：令d[i][j]代表从第i个点到第j个点，不经过任何障碍物时的路径数（当然除了i和j）。那么我们总共需要k+2个点，包括k个障碍物点以及起点和终点。

首先我们算出从i点到j点的所有路径数，然后减掉经过障碍物的那些“坏”的路线。让我们看看如何计算“坏”的路线：枚举i和j之间的所有障碍物点i<l<j，那么从i到j的“坏”路径数就是所有d[i][l]和d[l][j]的乘积最后求和。再被总路径数减掉就是d[i][j]的结果。

我们已经知道计算总路径数的复杂度为，那么该解法的总复杂度为。

（译注：这段算法有问题，事实上可以用O(k^2)方法解决）

素数四元组的个数问题

给出n个数，从其中选出4个数，使它们的最大公约数为1，问总共有多少中取法。

我们解决它的逆问题：求最大公约数d>1的四元组的个数。

运用容斥原理，将求得的对于每个d的四元组个数的结果进行加减。

其中deg(d)代表d的质因子个数，f(d)代表四个数都能被d整除的四元组的个数。

求解f(d)时，只需要利用组合方法，求从所有满足被d整除的ai中选4个的方法数。

然后利用容斥原理，统计出所有能被一个素数整除的四元组个数，然后减掉所有能被两个素数整除的四元组个数，再加上被三个素数整除的四元组个数…

和睦数三元组的个数问题

给出一个整数。选出a, b, c (其中2<=a<b<c<=n)，组成和睦三元组，即：

· 或者满足，，

· 或者满足

首先，我们考虑它的逆问题：也就是不和睦三元组的个数。

然后，我们可以发现，在每个不和睦三元组的三个元素中，我们都能找到正好两个元素满足：它与一个元素互素，并且与另一个元素不互素。

所以，我们只需枚举2到n的所有数，将每个数的与其互素的数的个数和与其不互素的数的个数相乘，最后求和并除以2，就是要求的逆问题的答案。

现在我们要考虑这个问题，如何求与2到n这些数互素（不互素）的数的个数。虽然求解与一个数互素数的个数的解法在前面已经提到过了，但在此并不合适，因为现在要求2到n所有数的结果，分别求解显然效率太低。

所以，我们需要一个更快的算法，可以一次算出2到n所有数的结果。

在这里，我们可以使用改进的埃拉托色尼筛法。

· 首先，对于2到n的所有数，我们要知道构成它的素数中是否有次数大于1的，为了应用容斥原理，我们还有知道它们由多少种不同的素数构成。

对于这个问题，我们定义数组deg[i]：表示i由多少种不同素数构成，以及good[i]：取值true或false，表示i包含素数的次数小于等于1是否成立。

再利用埃拉托色尼筛法，在遍历到某个素数i时，枚举它在2到n范围内的所有倍数，更新这些倍数的deg[]值，如果有倍数包含了多个i，那么就把这个倍数的good[]值赋为false。

· 然后，利用容斥原理，求出2到n每个数的cnt[i]：在2到n中不与i互素的数的个数。

回想容斥原理的公式，它所求的集合是不会包含重复元素的。也就是如果这个集合包含的某个素数多于一次，它们不应再被考虑。

所以只有当一个数i满足good[i]=true时，它才会被用于容斥原理。枚举i的所有倍数i*j，那么对于i*j，就有N/i个与i*j同样包含i（素数集合）的数。将这些结果进行加减，符号由deg[i]（素数集合的大小）决定。如果deg[i]为奇数，那么我们要用加号，否则用减号。

程序实现：

 1 int n;
 2 bool good[MAXN];
 3 int deg[MAXN], cnt[MAXN];
 4 long long solve() {
 5          memset (good, 1, sizeof good);
 6          memset (deg, 0, sizeof deg);
 7          memset (cnt, 0, sizeof cnt);
 8          long long ans_bad = 0;
 9          for (int i=2; i<=n; ++i) {
10                  if (good[i]) {
11                           if (deg[i] == 0) deg[i] = 1;
12                           for (int j=1; i*j<=n; ++j) {
13                                    if (j > 1 && deg[i] == 1)
14                                             if (j % i == 0)
15                                                     good[i*j] = false;
16                                             else
17                                                     ++deg[i*j];
18                                    cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
19                           }
20                  }
21                  ans_bad += (cnt[i] - 1) * 1ll * (n - cnt[i] - 1);
22          }
23          return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
24 }