LeetCode 133. Clone Graph

原题链接在这里：https://leetcode.com/problems/clone-graph/description/

题目：

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

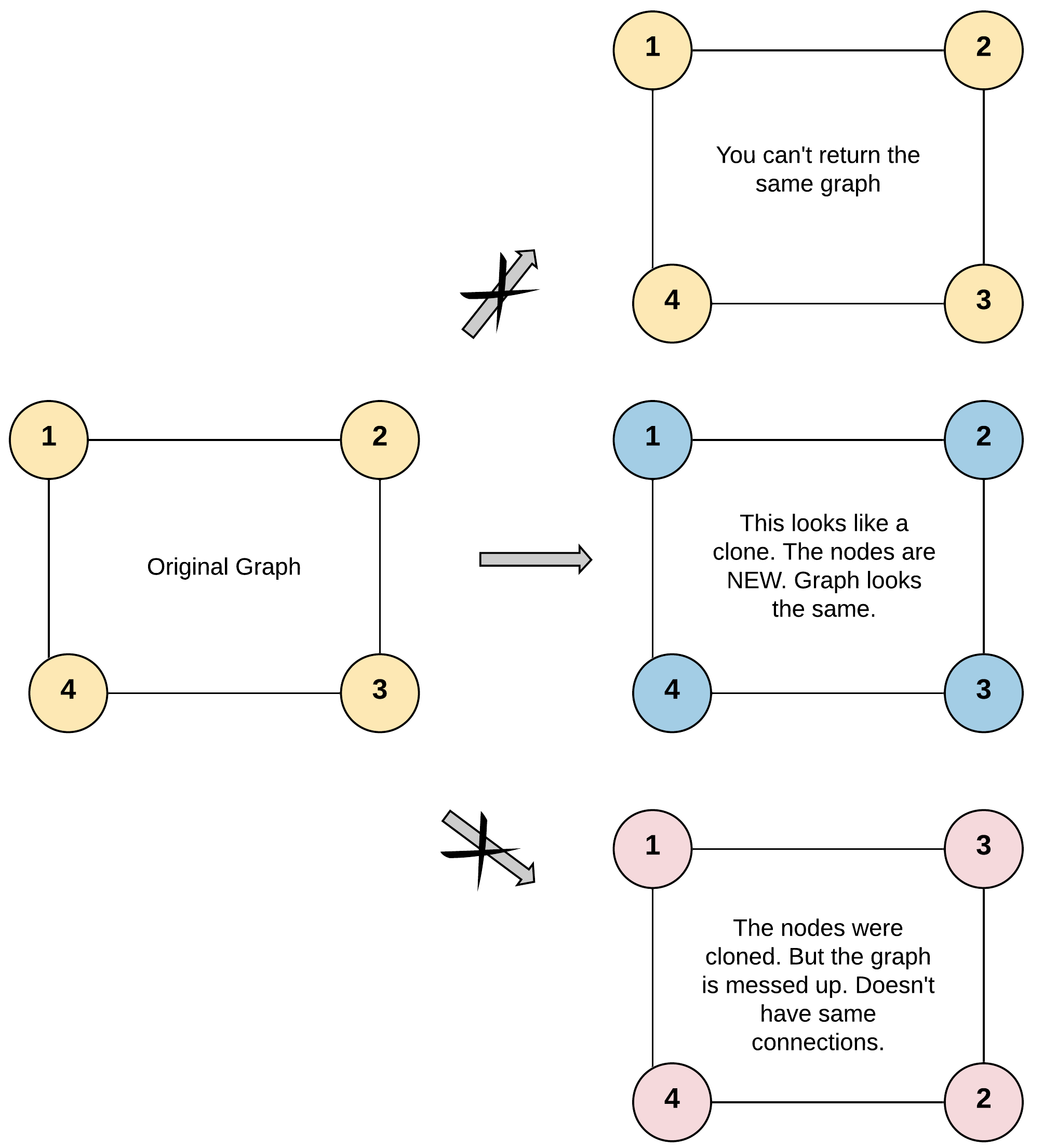
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

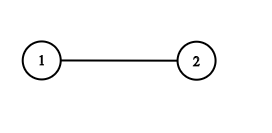
Input: adjList = [[2],[1]]
Output: [[2],[1]]

 

Constraints:

• 1 <= Node.val <= 100
• Node.val is unique for each node.
• Number of Nodes will not exceed 100.
• There is no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

题解：

复制原来的graph, 输入是一个graph node, 返回也是一个 graph node.

可以利用BFS, 同时维护HashMap hm 来记录visited 过的点. 以及 original node 和 copy node 的关系。

key存储原graph的node, value存用原node.label复制出来的node. 检查这个neighbor是不是已经在hm的key中了，如果已经在了就跳过，如果没在就加到queue中，并建立一个自身的copy组成键值对放入hm中。

同时更新当前节点currentNode 复制点 的neighbors list. 此时无论它的neighbor是否在hm中都应该把hm中对应这个heighbor key 的 value 放到 list中。

最后返回 以输入点的label复制的点。

Time Complexity: O(N+E). Space: O(N).

AC Java: 

/**
 * Definition for undirected graph.
 * class UndirectedGraphNode {
 *     int label;
 *     List<UndirectedGraphNode> neighbors;
 *     UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList<UndirectedGraphNode>(); }
 * };
 */
public class Solution {
    public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
        if(node == null){
            return node;
        }
        
        UndirectedGraphNode cloneNode = new UndirectedGraphNode(node.label);
        HashMap<UndirectedGraphNode, UndirectedGraphNode> visited = new HashMap<UndirectedGraphNode, UndirectedGraphNode>();
        visited.put(node, cloneNode);
        
        LinkedList<UndirectedGraphNode> que = new LinkedList<UndirectedGraphNode>();
        que.add(node);
        while(!que.isEmpty()){
            UndirectedGraphNode cur = que.poll();
            for(UndirectedGraphNode neighbor : cur.neighbors){
                if(!visited.containsKey(neighbor)){
                    UndirectedGraphNode cloneNeighbor = new UndirectedGraphNode(neighbor.label);
                    visited.put(neighbor, cloneNeighbor);
                    que.add(neighbor);
                }
                visited.get(cur).neighbors.add(visited.get(neighbor));
            }
        }
        
        return cloneNode;
    }
}

也可以DFS. 

Time Complexity: O(N+E). Space: O(N).

AC Java:

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/
class Solution {
    HashMap<Integer, Node> visited = new HashMap<>();
    
    public Node cloneGraph(Node node) {
        if(node == null){
            return node;
        }    
        
        if(visited.containsKey(node.val)){
            return visited.get(node.val);
        }
        
        Node copy = new Node(node.val);
        visited.put(node.val, copy);
        
        for(Node nei : node.neighbors){
            copy.neighbors.add(cloneGraph(nei));
        }
        
        return copy;
    }
}

类似Copy List with Random Pointer, Employee Importance.