2018年长沙理工大学第十三届程序设计竞赛
链接:https://www.nowcoder.com/acm/contest/96#question
持续更新ing,请多多关注~
A.LL
题目描述:
“LL是什么?这都不知道的话,别说自己是程序猿啊!” “longlong?” “。。。肯定是LoveLive啊!” qwb为了检验你是否是真正的程序猿,决定出道题考考你:现在程序会输入一行字符串,如果恰好是lovelive(不区分大小写)就输出yes,否则输出no。
输入描述:
输入有多组(组数不超过100),每组输入一行字符串(字符串长度不超过100)。
输出描述:
输出占一行,如果输入符合要求则输出yes,否则输出no。
示例1
输入
longlong
LoveLive
love live
输出
no
yes
no
代码实现如下:

1 #include <cstdio> 2 #include <string> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 string s; 9 10 int main() { 11 while(getline(cin, s)) { 12 int len = s.size(); 13 for(int i = 0; i < len; i ++) { 14 s[i] = tolower(s[i]); 15 } 16 if(s == "lovelive") printf("yes\n"); 17 else printf("no\n"); 18 } 19 }
B.奇怪的加法
题目描述:
zhrt是数学大佬,但有一天一道奇怪的数学题把他难住了:题目要求计算两个十进制数相加后的结果,但在本题中是不需要进位的! 现在zhrt弯下他的小蛮腰向你请教,你能帮帮他吗?
输入描述:
输入有多组(组数不超过1000),每组占一行,每行有2个正整数A和B。(A,B<=1e9)
输出描述:
每组输出占一行,输出题目中A和B相加的结果。
示例1
输入
123 321
999 1
99 11
输出
444
990
0
思路:本题模仿大数加,然后对每个和进行模10即可,记得去除前导零。
代码实现如下:

1 #include <cstdio> 2 #include <string> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 string a, b; 9 int c[15]; 10 11 int main() { 12 while(cin >>a >>b) { 13 int len1 = a.size(), len2 = b.size(), t = 0, flag = 0; 14 for(int i = len1 - 1, j = len2 - 1; ; i--, j--) { 15 if(i < 0 && j < 0) break; 16 if(i >= 0 && j >= 0) { 17 c[t] = (a[i] + b[j] - 2 * '0') % 10; 18 } else if(i >= 0 && j < 0) { 19 c[t] = (a[i] - '0') % 10; 20 } else if(j >=0 && i <0) { 21 c[t] = (b[j] - '0') % 10; 22 } 23 if(c[t] != 0) flag = 1; 24 t++; 25 } 26 if(flag == 0) { 27 printf("0\n"); 28 continue; 29 } else { 30 int l; 31 for(int i = t - 1; i >= 0; i--) { 32 if(c[i] != 0) { 33 l = i; 34 break; 35 } 36 } 37 for(int i = l; i >= 0; i--) { 38 printf("%d", c[i]); 39 } 40 printf("\n"); 41 } 42 } 43 }
C.取手机
题目描述:
durong有a台iphonex和b台s8,并且放在一个保险箱里,durong现在一台一台从保险箱随机拿出这些手机,现在他想知道第k次拿出s8的概率是多少
输入描述:
第一行一个正整数T,表示数据组数。(1<=T<=10000)接下来T行输入a,b,k其中(1<=a,b,k<=1e9) k<=a+b;
输出描述:
第k次拿出s8的概率,保留三位小数
示例1
输入
1
1 1 1
输出
0.500
思路:本题为组合数学的一个公式,比赛时自己智障了,在比赛十分钟左右的时候代码都写好了(当时公式是猜的),然后感觉不可能这么简单就没写了。将近两小时时,我就去去推了一下C题公式发现是对的,然后一边骂自己智障,一边把代码提交,然后就A了,不过记得是浮点数且小心爆int。公式推导如下图:
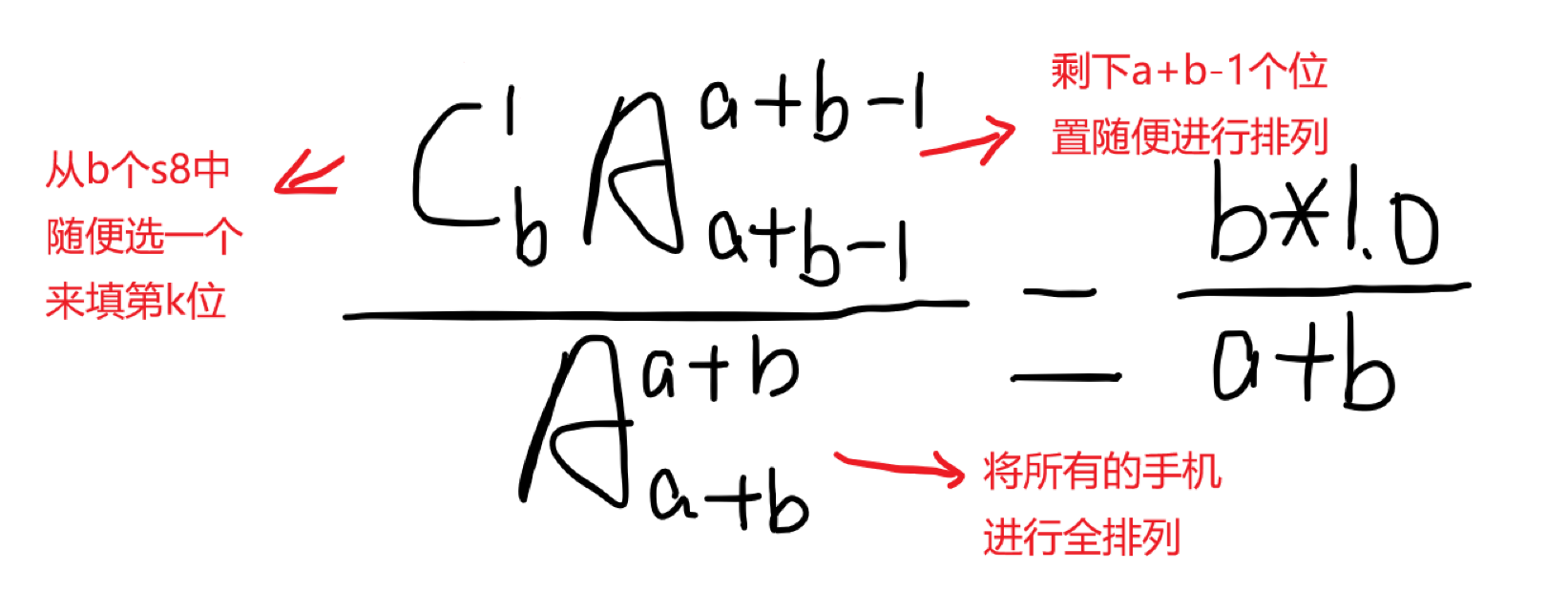

1 #include <cstdio> 2 3 int t; 4 long long a, b, k; 5 6 int main() { 7 scanf("%d", &t); 8 while(t--) { 9 scanf("%lld%lld%lld", &a, &b, &k); 10 printf("%.3f\n", b * 1.0 / (a + b)); 11 } 12 }
D.zzq的离散数学教室1
题目描述:
离散数学中有种名叫“哈斯图”的东西。 在这题中,你们需要计算的是一些正整数在偏序关系“整除”下的哈斯图的边数。用大白话讲,在偏序关系“整除”下的哈斯图,就是把一个个正整数看成一个个图的节点,某些节点之间有边。连边的规则是这样的:对于任意两个正整数a和b(a<b)来说,如果b%a==0,并且不存在一个正整数c(a<c<b),使得条件b%c==0和c%a==0同时成立,那么我们就在节点a和节点b之间连一条边。 现在问题是,给你们2个数L,R(1<=L,R<=1e6)。求由L,L+1,L+2...R这R-L+1个正整数在偏序关系“整除”下的哈斯图的边数。 比如L=1,R=4,节点的组合有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)。组合(1,2),(1,3),(2,4)可以连边。(1,4)因为中间存在c=2,不符合连边条件。所以当L=1,R=4的时候,这个哈斯图有3条边。
输入描述:
多组输入,不超过1000组数据每组数据一行,包含2个正整数L和R,中间由空格分开。
输出描述:
每组数据输出一行,包含一个整数表示哈斯图的边数。
示例1
输入
1 4
4 10
1 10
输出
3
2
11
备注:
哈斯图(英语Hasse发音为/ˈhæsə/,德语: /ˈhasə/)、在数学分支序理论中,是用来表示有限偏序集的一种数学图表,它是一种图形形式的对偏序集的传递简约。具体的说,对于偏序集合(S,≤),把S的每个元素表示为平面上的顶点,并绘制从x到y向上的线段或弧线,只要y覆盖x(就是说,只要x < y并且没有z使得x < z < y)。这些弧线可以相互交叉但不能触及任何非其端点的顶点。带有标注的顶点的这种图唯一确定这个集合的偏序。
思路:本题就是将[l,r]中所有数的素数倍并落在该区间中的个数相加即可,不过需要稍微处理一下,不然会T。

1 #include <cstdio> 2 #include <vector> 3 using namespace std; 4 5 const int maxn = 1e6 + 7; 6 int l, r; 7 int p[maxn]; 8 9 vector<int> v; 10 11 void init() { 12 for(int i = 0; i < maxn; i++) { 13 p[i] = 1; 14 } 15 p[0] = p[1] = 0; 16 for(int i = 2; i * i < maxn; i++) { 17 if(p[i]) { 18 for(int j = i * i; j < maxn; j += i) { 19 p[j] = 0; 20 } 21 } 22 } 23 for(int i = 2; i < maxn; i++) { 24 if(p[i]) v.push_back(i); 25 } 26 } 27 28 int main() { 29 init(); 30 while(~scanf("%d%d", &l, &r)) { 31 int ans = 0; 32 for(int j = 0; j < v.size(); j++) { 33 //所有[l,r]内的倍数落在该区间的数可以通过下面方法求出来,即a * b <= c,那么可以转化成a <= c/b; 34 if(r / v[j] - l + 1 > 0) ans += r / v[j] - l + 1; 35 else break; 36 } 37 printf("%d\n", ans); 38 } 39 }
E.小木乃伊到我家
题目描述:
AA的欧尼酱qwb是个考古学家,有一天qwb发现了只白白圆圆小小的木乃伊,它是个爱哭鬼却很努力。qwb想把这么可爱的小木乃伊送给 AA,于是便找上了快递姐姐,这下可让快递姐姐犯愁了,因为去往AA家的路实在太难走了(甚至有可能没有路能走到AA家),快递姐姐 找上聪明的ACMer,想请你帮忙找出最快到达AA家的路,你行吗?
输入描述:
第一行输入两个整数n和m(2<=n<=m<=200000),分别表示有n座城市和m条路,城市编号为1~n(快递姐姐所在城市为1,AA所在城市为n)。接下来m行,每行输入3个整数u,v,w(u,v<=n,w<=100000),分别表示城市u和城市v之间有一条长为w的路。
输出描述:
输出结果占一行,输出快递姐姐到达AA家最短需要走多远的路,如果没有路能走到AA家,则输出“qwb baka”(不用输出双引号)。
示例1
输入
4 4
1 2 1
2 3 2
3 4 3
2 3 1
输出
5
思路:裸的最短路……

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 5 const int maxn = 2e5 + 7; 6 const int inf = 0x3f3f3f3f; 7 8 int n, m; 9 int d[maxn]; 10 11 struct node { 12 int from, to, cost; 13 }edge[maxn]; 14 15 void short_path(int s) { 16 memset(d, inf, sizeof(d)); 17 d[1] = 0; 18 while(1) { 19 bool update = false; 20 for(int i = 0; i < m; i++) { 21 node e = edge[i]; 22 if(d[e.from] < inf && d[e.to] > d[e.from] + e.cost) { 23 d[e.to] = d[e.from] + e.cost; 24 update = true; 25 } 26 if(d[e.to] < inf && d[e.from] > d[e.to] + e.cost) { 27 d[e.from] = d[e.to] + e.cost; 28 update = true; 29 } 30 } 31 if(!update) break; 32 } 33 } 34 35 int main() { 36 while(~scanf("%d%d", &n, &m)) { 37 for(int i = 0; i < m; i++) { 38 scanf("%d%d%d", &edge[i].from, &edge[i].to, &edge[i].cost); 39 } 40 short_path(1); 41 if(d[n] >= inf) printf("qwb baka\n"); 42 else printf("%d\n", d[n]); 43 } 44 }
F.箱庭的股市(待补)
题目描述
有一天qwb收到来自箱庭的邀请函,准备打倒魔王的qwb来到箱庭后却迷上了炒股。箱庭的股市为了不让股民亏钱便设立了一个有趣的机制:设A[i][j]为qwb所持有的股票第i天第j秒的价格,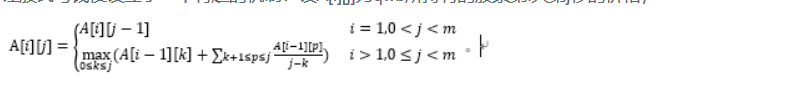
需要注意的是作为异世界的箱庭时间有些奇怪,在箱庭里一天有m秒。由于qwb急需用钱,因此qwb要把股票卖了,他想知道卖股票时自己所持股票的价格,你能帮他算出来吗?
输入描述:
每组的输出占一行,输出qwb所持股票在第x天的第y秒时的价格。输入有多组(组数不超过20000)。每组占一行,输入4个整数m,x,y,p(0<m<=1e4,0<=x <=1e6,0<=y<m,0<p<=1e6),分别表示箱庭的一天有m秒,qwb要在第x天的第y秒卖掉股票,qwb所持股票在第1天的第0秒的价格为p。
输出描述:
每组的输出占一行,输出qwb所持股票在第x天的第y秒时的价格,结果对1e9 + 7取模。
示例1
输入
3 2 2 1
输出
2
G.逃离迷宫
题目描述:
给你一个n*m的图,地图上'.'代表可以走的地方,而'#'代表陷阱不能走, 'P'代表人物位置,'K'代表钥匙,'E'代表出口。人物一个,钥匙有多个, ('K'的数量<=50)),出口一个,每个位置可以向(上,下,左,右)四个 方向走一格,花费一个单位时间,现在你需要花费最少的时间拿到钥匙 然后从迷宫的出口出去(若没有钥匙,则不能进入迷宫出口所在的格子)。
输入描述:
第一行一个整数T(T <= 50),代表数据的组数接下来一行n,m(n<=500,m<=500),代表地图的行和列接下来n行,每行一个长度为m的字符串,组成一个图。
输出描述:
如果可以出去,输出所花费的最少时间。如果不能出去,输出一行"No solution"。
示例1
输入
3
5 5
....P
##..E
K#...
##...
.....
5 5
P....
.....
..E..
.....
....K
5 5
P#..E
.#.#.
.#.#.
.#.#.
...#K
输出
No solution
12
No solution
思路:比较裸的bfs,不过不要采取用vis数组来标记当前点是否已经访问过,因为如果处理不当极容易T,第一场湖南多校赛的血的教训。对于这种,我建议采用最短路中的松弛思想。
代码实现如下:

1 #include <cstdio> 2 #include <queue> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 const int inf = 3e4 + 7; 8 9 int t, n, m, ans; 10 int s[505][505], e[505][505]; 11 char mp[505][505]; 12 13 struct node { 14 int x, y; 15 }nw, nxt; 16 17 int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1}; 18 19 void bfs1(int x, int y) { 20 nw.x = x, nw.y = y; 21 s[x][y] = 0; 22 queue<node> q; 23 q.push(nw); 24 while(!q.empty()) { 25 nw = q.front(), q.pop(); 26 for(int i = 0; i < 4; i++) { 27 nxt.x = nw.x + dx[i], nxt.y = nw.y + dy[i]; 28 if(nxt.x >= 0 && nxt.x < n && nxt.y >= 0 && nxt.y <m && mp[nxt.x][nxt.y] != '#' && mp[nxt.x][nxt.y] != 'E') { 29 if(s[nxt.x][nxt.y] > s[nw.x][nw.y] + 1) { 30 s[nxt.x][nxt.y] = s[nw.x][nw.y] + 1; 31 q.push(nxt); 32 } 33 } 34 } 35 } 36 } 37 38 void bfs2(int x, int y){ 39 nw.x = x, nw.y = y; 40 e[x][y] = 0; 41 queue<node> q; 42 q.push(nw); 43 while(!q.empty()) { 44 nw = q.front(), q.pop(); 45 for(int i = 0; i < 4; i++) { 46 nxt.x = nw.x + dx[i], nxt.y = nw.y + dy[i]; 47 if(nxt.x >= 0 && nxt.x < n && nxt.y >= 0 && nxt.y <m && mp[nxt.x][nxt.y] != '#') { 48 if(e[nxt.x][nxt.y] > e[nw.x][nw.y] + 1) { 49 e[nxt.x][nxt.y] = e[nw.x][nw.y] + 1; 50 q.push(nxt); 51 } 52 } 53 } 54 } 55 } 56 57 int main() { 58 scanf("%d", &t); 59 while(t--) { 60 scanf("%d%d", &n, &m); 61 for(int i = 0; i < n; i++) { 62 scanf("%s", mp[i]); 63 } 64 memset(s, inf, sizeof(s)); 65 memset(e, inf, sizeof(e)); 66 for(int i = 0; i < n; i++) { 67 for(int j = 0; j < m; j++) { 68 if(mp[i][j] == 'P') { 69 bfs1(i,j); 70 } 71 if(mp[i][j] == 'E') { 72 bfs2(i,j); 73 } 74 } 75 } 76 ans = inf; 77 for(int i = 0; i < n; i++) { 78 for(int j = 0; j < m; j++) { 79 if(mp[i][j] == 'K') { 80 ans = min(s[i][j] + e[i][j], ans); 81 } 82 } 83 } 84 if(ans >= inf) printf("No solution\n"); 85 else printf("%d\n", ans); 86 } 87 }
H.数学考试
题目描述:
今天qwb要参加一个数学考试,这套试卷一共有n道题,每道题qwb能获得的分数为ai,qwb并不打算把这些题全做完, 他想选总共2k道题来做,并且期望他能获得的分数尽可能的大,他准备选2个不连续的长度为k的区间, 即[L,L+1,L+2,....,L+k-1],[R,R+1,R+2,...,R+k-1](R >= L+k)。
输入描述:
第一行一个整数T(T<=10),代表有T组数据接下来一行两个整数n,k,(1<=n<=200,000),(1<=k,2k <= n)接下来一行n个整数a1,a2,...,an,(-100,000<=ai<=100,000)
输出描述:
输出一个整数,qwb能获得的最大分数
示例1
输入
2
6 3
1 1 1 1 1 1
8 2
-1 0 2 -1 -1 2 3 -1
输出
6
7
代码实现如下:

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int inf = 1e9 + 7; 4 const int maxn = 1e5 + 10; 5 struct node { 6 int num, id; 7 } qu[2 * maxn]; 8 int cmp(node a, node b) { 9 return a.num > b.num; 10 } 11 int a[2 * maxn]; 12 int sum[2 * maxn]; 13 int main() { 14 int n, t,k; 15 scanf("%d", &t); 16 while(t--) { 17 scanf("%d%d", &n, &k); 18 memset(sum, 0, sizeof(sum)); 19 20 for (int i = 0 ; i < n ; i++) { 21 scanf("%d", &a[i]); 22 } 23 long long m=0,sum1=0,sum2; 24 for(int i=0;i<k;i++) 25 { 26 m+=a[i]; 27 } 28 sum1=m; 29 sum2=0; 30 for(int i=k;i<2*k;i++) 31 { 32 sum2+=a[i]; 33 } 34 long long ans=m+sum2; 35 36 for(int i=k;i+k-1<n-1;i++) 37 { 38 sum1-=a[i-k]; 39 sum1+=a[i]; 40 m=max(sum1,m); 41 sum2-=a[i]; 42 sum2+=a[i+k]; 43 // cout<<m<<endl; 44 // cout<<sum1<<" "<<sum2<<endl; 45 if(m+sum2>ans)ans=m+sum2; 46 } 47 cout<<ans<<endl; 48 } 49 return 0; 50 }
I.连续区间的最大公约数(待补)
题目描述:
给一个数列共n(n<=100,000)个数,a1,a2,...,an.(0<=ai<=1000,000,000).有q(q<=100,000)个询问。每个询问为l,r(1<=l<=r<=n).求gcd(al,al+1,...,ar). 再求区间[l,r]的子区间中(l<=l'<=r'<=r)满足gcd(al,al+1,...,ar) = gcd(al',al'+1,...ar')的子区间个数.
输入描述:
第一行一个数T表示数据组数第二行一个数n接下来一行n个数,a1,a2,...,an接下一行一个数q接下来一行2个数l和r。
输出描述:
首先输出一行“Case #:t”,t代表当前是第几组数据。接下来q行,每行输出2个数,第一个是gcd(al,al+1,...,ar),第二个是区间[l,r]的子区间中(l<=l'<=r'<=r)满足gcd(al,al+1,...,ar) = gcd(al',al'+1,...ar')的子区间个数。
示例1
输入
2
5
1 2 4 6 7
4
1 5
2 4
3 4
4 4
5
1 2 4 2 1
6
1 1
1 3
2 2
2 3
2 4
3 3
输出
Case #1:
1 8
2 4
2 1
6 1
Case #2:
1 1
1 3
2 1
2 2
2 5
4 1
J.杯子(待补)
题目描述:
一天durong同学买了一个无限长的杯子,同时买了n个球,并且标号为1,2,3......n,durong同学突然想到一个问题----如果他把n个球依次,也就是按照1,2,3...n的顺序放进杯子里,然后在全部拿出来(注意不一定要等到全部放进去才能拿出球),并且会记录放进和拿出球的顺序, durong想知道,要满足当第m个球进去后,杯子中此时恰好有k个球,然后仍然要把剩下的n-m个球放进去,最后杯中的球要取光,这样的放进和拿出球的顺序有多少种,答案有可能很大,所以mod上1e9+7
输入描述:
1<=n,m,k<=1e6(m可能大于n,k可能大于m)第一行一个正整数T,表示数据组数。(1<=T<=10000)对于每组数据包含一行三个正整数n,m,k。
输出描述:
对于每组数据输出一个正整数表示答案。由于答案可能过大,所以只需要输出对1e9+7取模后的答案
示例1
输入
2
3 3 3
3 3 2
输出
1
2
K.zzq的离散数学教室2(待补)
题目描述:
离散数学中有种名叫“偏序集”的东西。
在这个题目中,集合中有n个元素,编号从1到n。它们之间共有m对偏序关系(1<=m<=2n),每一对偏序关系的表示形式为以空格分开的两个编号:x y。含义是x和y之间有关系≤。(这里的≤不是传统意义上的小于等于,可以理解为从y到x的一条有向边),记做:x≤y。同时这些关系也具有传递性,例如,如果x≤y并且y≤z,那么可以得到x≤z。数据保证不会出现同时有x≤y,y≤z,z≤x的情况。
现在我们的问题是,要你从n个元素里尽可能多的选出一些元素,使得这些元素之间不满足偏序关系。(即这些点中,任意两点都不存在偏序关系).问你最多能选几个元素。
输入描述:
第一行一个数T,代表有T组数据下一行,包含2个正整数n和m,中间由空格分开。(2<=n<=100,000,n的总和 <= 300,000)接下来m行,为m个偏序关系,每行2个整数x和y,即表示编号为x的元素和编号为y的元素有关系:x≤y
输出描述:
每组数据输出一行,每行一个整数,最多能选的元素数量。
示例1
输入
1
5 5
1 2
2 3
2 4
2 5
4 5
输出
2
备注:
偏序集在百度百科上的定义是这样的:设R为非空集合A上的关系,如果R是自反的、反对称的和可传递的,则称R为A上的偏序关系,简称偏序,通常记作≦。一个集合A与A上的偏序关系R一起叫作偏序集,记作或。其中(自反性)对任一,则x≦x;(反对称性)如果x≦y,且y≦x,则x=y;(传递性)如果x≦y,且y≦c ,则x≦c。
L.仓鼠养殖计划
题目描述:
集训队暑训的时候,是睡在机房的,有几个小伙子不甘寂寞,带了仓鼠来机房。有的还不止带了一只! 为此,贴心的集训队刘队长买了一大一小两种放仓鼠笼子的架子,大的可以放两个仓鼠笼 小的只能放一个。 要注意的是仓鼠是领地动物,一般来讲 仓鼠笼与仓鼠笼之间是不能贴在一起的, 但同一个人带来的仓鼠的仓鼠笼可以被放在一起(既两个仓鼠笼如果属于同一个人,那么这两个仓鼠笼就可以被放在同一个大架子上) 现在告诉你现有的两种架子的数量和多少人带了仓鼠以及每个人带的仓鼠的数量,问你是否能将这些仓鼠放下。
输入描述:
第一行为一个数T 表示测试样例组数对于每组测试数据第1行输入a,b,n; 分别为小架子的数量,大架子的数量,带了仓鼠的人数第2行有n个数字P1-Pn,分别表示每个人带的仓鼠的数量
输出描述:
如果放得下 则输出"Yes" 否则输出"No"
示例1
输入
1
1 2 4
1 1 1 1
输出
No
备注:
1<=n<=50 1<=a,b<=100 1<=Pi<=20
代码实现如下:

1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 5 int t, a, b, n; 6 int p[55]; 7 8 bool cmp(int a, int b) { 9 return a > b; 10 } 11 12 int main() { 13 scanf("%d", &t); 14 while(t--) { 15 scanf("%d%d%d", &a, &b, &n); 16 for(int i = 0; i < n; i++) { 17 scanf("%d", &p[i]); 18 } 19 sort(p, p + n, cmp); 20 for(int i = 0; i < n; i++) { 21 while(p[i] > 0) { 22 if(p[i] >=2 && b > 0) { 23 p[i] -= 2; 24 b--; 25 continue; 26 } else if(p[i] >=1) { 27 p[i]--; 28 if(a > 0) { 29 a--; 30 } else { 31 b--; 32 } 33 } 34 } 35 } 36 if(a < 0 || b < 0) printf("No\n"); 37 else printf("Yes\n"); 38 } 39 }


