Codeforces Round #483 (Div. 2)

Link

A.B

按题意模拟即可

---

C

题意

给出分数p/q，问p/q在b进制下是否为无限循环小数(p,q,b<=10^18)

分析

考虑进制转化过程，若1/q在b进制下为有限小数，则p/q也一定是，那么考虑小数的进制转化，不断的×b，去掉整数，取小数部分继续×b，直至小数部分为0，即(b^k%q）==0，那么b^k的质因子和b完全相同，即b必须有q的全部因子才是有限小数，故不断q/gcd(q,b)直至q为1即可

#include<bits/stdc++.h>
#define ll long long
using namespace std;

int t;
ll p,q,b;

ll gcd(ll a, ll b){
     return b==0?a:gcd(b,a%b);
}
int main()
{

    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%lld%lld",&p,&q,&b);
        ll ans=gcd(p,q);
        q=q/ans,p=p/ans;
        if(p%q==0)
            printf("Finite\n");
        else{
            while(q!=1&&b!=1)
            {
                b=gcd(b,q);
                q/=b;
            }
            if(q==1)printf("Finite\n");
            else printf("Infinite\n");
        }
    }
    return 0;
}

---

D    solved

题意

定义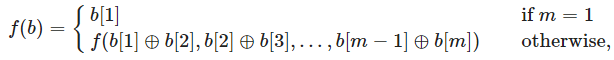，给一个长度为n的数组a，a的一个子区间[l,r]，f[l,r]定义为对该子区间执行f操作的值。定义ans[l,r]为满足l<=i<=j<=r的f[i,j]的最大值，q询问区间 ans[l,r] 的最大值    (n<=5000,q<=1e5,a[i]<=2^30-1)

分析

不难看出，f[i][j] = f[i][j-1] ^ f[i+1][j]，ans[i][j]=max(ans[i][j],max(ans[i+1][j],ans[i][j-1])),区间dp思想，枚举区间长度递推过去即可

#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int maxn=5000+7;

int n,q,l,r,dp[maxn][maxn],f[maxn][maxn],a[maxn];

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        dp[i][i]=f[i][i]=a[i];
    }
    for(int len=2;len<=n;len++){
        for(int j=1;j+len-1<=n;j++){
            f[j][j+len-1]=f[j+1][j+len-1]^f[j][j+len-2];
        }
    }
    for(int len=2;len<=n;len++){
        for(int j=1;j+len-1<=n;j++)
            dp[j][j+len-1]=max(f[j][j+len-1],max(dp[j][j+len-2],dp[j+1][j+len-1]));
    }
    scanf("%d",&q);
    while(q--){
        scanf("%d%d",&l,&r);
        printf("%d\n",dp[l][r]);
    }
    return 0;
}