2017-2018 ACM-ICPC Pacific Northwest Regional Contest (Div. 1)

Time：2018.4.14 8:00-13:00

Link

A sovled by ym&czh

题意

ym：签到，写复杂了，偶数回文串必定存在相邻相同，故可直接判断

题意

有 $n$

分析

C solved by czh&ym

题意

定义F(n)：n的因子和，给出a，b，求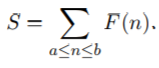(1 ≤ a ≤ b ≤ 1e12，b− a ≤ 1e6 ).

分析

czh : 枚举约数1到√b 的贡献，同时用等差数列求和的方法，求出大于√b一侧的贡献，当时知道另一侧会有贡献，但是没想到另一侧是等差数列，思考不够深入

D solved by ym

题意

给一颗n个节点的树，n-1条边，每条边都被染色，定义彩虹路径为：路径上不存在相邻的边是同一种颜色，定义一条边为good：到达这个点的所有路径都为彩虹路径，问那些点是good点，输出编号

分析

ym：经典树上做标记题，通过画成树形图观察不难发现，相邻的边的颜色相同

按照父节点是否相同可以分为两类

显然父节点相同的情况是：这两个儿子以及子树全部不符合

父节点不同（即一个点是另一个点的爷爷(父亲的父亲) ): 这种情况显然除了连接这两个点的点的子树(除去颜色相同的点)，其余的点全部不符合

那么问题转化为：树上的一个节点如何打标记，使得我们可以找到符合条件的点，即一个节点的子树有哪些点，显然可以想到从一个节点递归的时候，一个节点访问的就时它的子树

所以我们可以任意选取一点为根，按照dfs序为记录每个节点的开始值(即该节点的值)，和该点子树的范围(即子树节点个数)

那么现在我们所有问题全部解决，直接访问所有节点的边一次，差分前缀和打标记即可

#include<bits/stdc++.h>
#define ll long long
#define sc scanf
#define pr printf
#define rep(i,s,e) for(int i=s;i<=e;i++)
using namespace std;
const int maxn = 1e5+7;
const int mod=1e9+7;
int n;
int head[maxn*2],nxt[maxn*2],to[maxn*2],c[maxn*2],tot;
int st[maxn],ed[maxn],ans,f[maxn],orr[maxn*2], sum[maxn];
pair<int,int>g[maxn];

void add(int u,int v,int z)
{
    c[++tot]=z;
    to[tot]=v;
    nxt[tot]=head[u];
    head[u]=tot;
}

void dfs(int now, int fa)
{
    f[now]=fa;
    st[now]=++ans;
    for(int i=head[now];i;i=nxt[i])
    {
        if(to[i]!=fa)
            dfs(to[i], now);
    }
    ed[now]=ans;
}

int main()
{
    sc("%d",&n);
    int u, v, val;
    rep(i,1,n-1)
    {
        sc("%d%d%d", &u, &v, &val);
        add(u,v,val), add(v,u,val);
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
    {
        int t=0;
        for(int j=head[i];j;j=nxt[j])
            g[++t]=make_pair(c[j],to[j]);
        sort(g+1,g+t+1);
        int k;
        for(int j=1;j<=t;j=k)
        {
            for(k=j;k<=t&&g[j].first==g[k].first;k++);
            if(k>j+1)
            {
               for(int w=j;w<k;w++)
               {
                   int y=g[w].second;
                   if(y==f[i])
                   {
                       sum[1]++;
                       sum[st[i]]--;
                       sum[ed[i]+1]++;
                   }
                   else
                   {
                       sum[st[y]]++;
                       sum[ed[y]+1]--;
                   }
               }
            }
        }
    }
    int answer=0;
    for(int i=1;i<=n;i++)
    {
        sum[i]+=sum[i-1];
        if(!sum[i])
            answer++;
    }
    printf("%d\n", answer);
    for(int i=1;i<=n;i++) if(!sum[st[i]]) pr("%d\n", i);
    return 0;
}

E solved by czh

题意

物理题，czh秒了

几何，留坑

G make up by ym &czh

题意

给出n个房间和m扇门，共有k个人，每扇门可以从A_i到Bi，并且编号为Ci~Di的人都可以通过，给出S、T，问有多少人可以从S到T

(2 ≤ n ≤ 1,000; 1 ≤ m ≤ 5,000; 1 ≤ k ≤ 1e9 ) ( 1 ≤ s, t ≤ n; s != t) (1 ≤ ai , bi ≤ n; 1 ≤ ci ≤ di ≤ k; ai != bi)

分析

ym：将区间离散化，最多只有2m个数，考虑每次枚举一个数，则对于所有门的下界一定不会小于当前数比第一小的数，对O(m)进行暴力判断即可，时间复杂度O(m(n+m))

Trick：由于每次检查的区间为[ q[i-1]+1，q[i]]，假设q[i-1]是某个区间的左端点，那么必然是要减1的，反之q[i-1]是某个区间的右端点，不管q[i-1]是否合法，我们都不应该修改

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=10010;
int n,m,k,S,T,i,j,cnt,q[N],K;
int g[N],ed,v[N],vc[N],vd[N],nxt[N],vis[N],ans;
inline void add(int x,int y,int c,int d){
    v[++ed]=y;
    vc[ed]=c;
    vd[ed]=d;
    nxt[ed]=g[x];
    g[x]=ed;
}
void dfs(int x){
    if(vis[x])return;
    vis[x]=1;
    for(int i=g[x];i;i=nxt[i])if(vc[i]<=K&&K<=vd[i])dfs(v[i]);
}
int main(){
    scanf("%d%d%d%d%d",&n,&m,&k,&S,&T);
    for(i=1;i<=m;i++){
        int a,b,c,d;
        scanf("%d%d%d%d",&a,&b,&c,&d);
        add(a,b,c,d);
        q[++cnt]=c-1;
        q[++cnt]=d;
    }
    sort(q+1,q+cnt+1);
    for(i=2;i<=cnt;i++)if(q[i]!=q[i-1]){
        K=q[i];
        for(j=1;j<=n;j++)vis[j]=0;
        dfs(S);
        if(vis[T])ans+=q[i]-q[i-1];
    }
    printf("%d",ans);
}

题意

分析

dp+斜率优化+维护凸壳，留坑

题意

分析

大模拟，留坑

J solve by czh&ym

题意

给一个有n×m个格子的长方形，每个格子可以填B/R，若某个格子是B，则它的左上方全为B，现给出n，m，和一部分已经填充好的，问所有方案数(n,m <= 30)

分析

ym:赛时：辣鸡ym，定义dp[i][j][0/1]：表示格子(i,j)是B/R的状态数，状态有问题，因为这样定义后面的状态显然会影响前面的状态，违背了“无后效性”（一个B前面的所有状态应该都为0)

赛后：dp[i][j]：表示第i行前j个位B和方案数，注意状态不要重复

#include<bits/stdc++.h>
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int maxn = 1e5+7;
const int mod=1e9+7;

ll dp[35][35];
char a[35][35];
int ok[35][35];
int n,m;

int init(int x,int y)
{
    for(int i=1;i<=y;i++) if(a[x][i]=='R') return 0;
    for(int i=y+1;i<=m;i++) if(a[x][i]=='B') return 0;
    return 1;
}

int main()
{
    sc("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        sc("%s", a[i]+1);
    for(int i=0;i<=m;i++)
        dp[1][i]=init(1,i);
    ll ans=0;
    if(n==1)
    {
        for(int i=0;i<=m;i++)
        {
            dp[1][i]=init(1,i);
            ans+=dp[1][1];
        }
        printf("%I64d\n", ans);
        return 0;

    }
    for(int i=2;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {

            for(int k=j;k<=m;k++)
            {

                    dp[i][j]+=dp[i-1][k]*init(i,j);
            }
            if(i==n)
                ans+=dp[n][j];
            //cout<<i<<' '<<j<<' '<<dp[i][j]<<endl;
        }
    }
    printf("%I64d\n", ans);
    return 0;
}

题意

分析

ym：dp，待补

L solved by ym

题意

签到

Summary

Ym：辣鸡ym卡题，学弟上去直接A掉，比赛时卡题，没有迅速换题换人，造成时间上失败，认真听队友建议

Czh:

posted @ 2018-04-14 18:31 Deadlined 阅读(342) 评论(0) 编辑收藏举报

刷新页面返回顶部

Deadline

2017-2018 ACM-ICPC Pacific Northwest Regional Contest (Div. 1)

公告