代码改变世界

动态规划求解0/1背包问题

2011-08-23 18:08  Daniel Zheng  阅读(2387)  评论(0)  编辑  收藏  举报

什么是动态规划？

动态规划是一种在数学和计算机科学中使用的，用于求解包含重叠子问题的最优化问题的方法。其基本思想是，将原问题分解为相似的子问题，在求解的过程中通过子问题的解求出原问题的解。动态规划的思想是多种算法的基础，被广泛应用于计算机科学和工程领域。比较著名的应用实例有：求解最短路径问题，背包问题，项目管理，网络流优化等。

动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。

动态规划只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足，故有时需要引入一定的近似)。简单地说，问题能够分解成子问题来解决。


实施动态规划的步骤：

  1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
  2. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

什么是0/1背包问题？

我们有n种物品，物品j的重量为wj，价格为pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。

如果限定每种物品只能选择0个或1个，则问题称为0-1背包问题。可以用公式表示为：

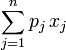
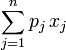
　　maximize \qquad \sum_{j=1}^n p_j\,x_j
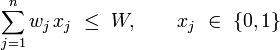
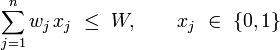
　　subject to \qquad \sum_{j=1}^n w_j\,x_j \ \le \ W, \quad \quad x_j \ \in \ \{0,1\} 

问题求解：

我们将在总重量不超过Y的前提下，前j种物品的总价格所能达到的最高值定义为A(j, Y)。

A(j, Y)的递推关系为：

  • A(0, Y) = 0
  • A(j, 0) = 0
  • 如果wj > Y, A(j, Y) = A(j - 1, Y)
  • 如果wj ≤ Y, A(j, Y) = max { A(j - 1, Y), pj + A(j - 1, Y - wj) }

通过计算A(n, W)即得到最终结果。为提高算法性能，我们把先前计算的结果存入表中。

　　下面给出代码：

 1 #include <iostream>
 2 #include <cstdlib>
 3 using namespace std;
 4 
 5 struct Item
 6 {
 7     void SetItem(int w, int v, bool s)
 8     {
 9         weight = w;
10         value = v;
11         selected = s;
12     }
13     int weight;
14     int value;
15     bool selected;
16 };
17 
18 
19 int Pick(Item goods[],int totalWeight,int amount)
20 {
21     int c[amount + 1][totalWeight + 1];
22 
23     for(int i = 0; i < amount + 1; ++i)
24         c[i][0] = 0;
25     for(int j = 0; j < totalWeight + 1; ++j)
26         c[0][j] = 0;
27 
28     for(int i = 1; i < amount + 1; ++i)
29         for(int j = 1; j < totalWeight + 1; ++j)
30         {
31             if(goods[i].weight < j + 1)
32                 c[i][j] = max(c[i - 1][j], c[i - 1][j - goods[i].weight] + goods[i].value);
33             else
34                 c[i][j] = c[i - 1][j];
35         }
36 
37     for(int i = 0; i < amount + 1; ++i)
38     {
39         for(int j = 0; j < totalWeight + 1; ++j)
40         {
41             cout<<"\t"<<c[i][j]<<" ";
42         }
43         cout<<endl;
44     }
45 
46     for(int i = amount, j = totalWeight; i > 0; --i)
47     {
48         if(c[i][j] > c[i - 1][j])
49         {
50             goods[i].selected = true;
51             j = j - goods[i].weight;
52         }
53     }
54 
55     return c[amount][totalWeight];
56 
57 }
58 
59 int main()
60 {
61     int amount = 5;
62     int totalWeight = 10;
63     Item * goods = new Item[amount + 1];
64     goods[0].SetItem(0, 0, false);
65     goods[1].SetItem(2, 6, false);
66     goods[2].SetItem(2, 3, false);
67     goods[3].SetItem(6, 5, false);
68     goods[4].SetItem(5, 4, false);
69     goods[5].SetItem(4, 6, false);
70 
71     int value = Pick(goods, totalWeight, amount);
72 
73     cout<<"Max value is "<<value<<endl;
74     cout<<"Good picked are :"<<endl;;
75     for(int i = 0; i < amount + 1; ++i)
76     {
77         if(goods[i].selected)
78             cout<<"index = "<<i<<" -> "<<"weight = "<<goods[i].weight<<" "<<"value = "<<goods[i].value<<endl;;
79     }
80 
81     delete [] goods;
82     return 0;
83 }