【LCA最近公共祖先】在线离线
【在线】
1.倍增法
现将深度较大的跳至与深度较小的统一深度。预处理$fa[u][i]$表示$u$往上跳$2^i$个单位后的祖先，则就可以像快速幂一样，将移动的步数化为二进制，如果第$i$位为$1$，那么向上跳$2^i$次方，即$if(1 << i \& d) u = fa[u][i]$。跳至统一深度后，若两点重合，则返回两点的任意一个。若不重合，再一个一个一起往上跳，直到重合。
复杂度为$O(N*logN) $
【code】求两点距离
#include<iostream> #include<cstring> #include<string> #include<algorithm> #include<cmath> #include<cstdio> #include<cstdlib> using namespace std; const int N = 100050; int dep[N], dis[N]; int ecnt, adj[N], go[N << 1], len[N << 1], nxt[N << 1]; int fa[N][20], Log[N], n, m; inline void addEdge(const int &u, const int &v, const int &l){ nxt[++ecnt] = adj[u], adj[u] = ecnt, go[ecnt] = v, len[ecnt] = l; nxt[++ecnt] = adj[v], adj[v] = ecnt, go[ecnt] = u, len[ecnt] = l; } inline void Init_Log(){ Log[0] = -1; for(int i = 1; i <= n; i++) Log[i] = Log[i >> 1] + 1; } inline void dfs(const int &u, const int &f, const int &l){ dep[u] = dep[f] + 1; dis[u] = dis[f] + l; fa[u][0] = f; for(int i = 0; fa[u][i]; i++) fa[u][i + 1] = fa[fa[u][i]][i]; for(int e = adj[u]; e; e = nxt[e]){ int v = go[e]; if(v == f) continue; dfs(v, u, len[e]); } } inline int lca(int u, int v){ if(dep[u] < dep[v]) swap(u, v); int delta = dep[u] - dep[v]; for(int i = Log[delta]; i >= 0; i--) if(1 << i & delta) u = fa[u][i]; if(u == v) return u; for(int i = Log[dep[u]]; i >= 0; i--) if(fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i]; return fa[u][0]; } int main(){ scanf("%d%d", &n, &m); Init_Log(); for(int i = 1; i < n; i++){ int x, y, z; scanf("%d%d%d", &x, &y, &z); addEdge(x, y, z); } dfs(1,0,0); for(int i = 1; i <= m; i++){ int x, y; scanf("%d%d", &x, &y); int L = lca(x, y); cout<<(dis[x] - dis[L]) + (dis[y] - dis[L])<<endl; } return 0; }
2.树链剖分
同样，将点往上跳，不过树链剖分后可以直接从重链尾部跳到重链顶部甚至下一条重链的尾部，直到两点在同一重链上，先判重合，否则就是现在深度较小的点。
复杂度O(mlog2 n)
【code】求两点距离
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<cmath> using namespace std; const int N = 1e5 + 50; const int oo = 0x3f3f3f3f; int dep[N], sze[N], top[N], son[N], pos[N], idx[N], val[N], fa[N]; int ecnt, adj[N], go[N << 1], nxt[N << 1], tot, len[N << 1]; int n, m, dis[N]; inline int Re(){ int i = 0, f = 1; char ch = getchar(); for(; (ch < '0' || ch > '9') && ch != '-'; ch = getchar()); if(ch == '-') f = -1, ch = getchar(); for(; ch >= '0' && ch <= '9'; ch = getchar()) i = (i << 3) + (i << 1) + (ch - '0'); return i * f; } inline void Wr(int x){ if(x < 0) putchar('-'), x = -x; if(x > 9) Wr(x / 10); putchar(x % 10 + '0'); } inline void addEdge(const int &u, const int &v, const int &l){ nxt[++ecnt] = adj[u], adj[u] = ecnt, go[ecnt] = v, len[ecnt] = l; nxt[++ecnt] = adj[v], adj[v] = ecnt, go[ecnt] = u, len[ecnt] = l; } inline void dfs1(const int &u, const int &f, const int &l){ dep[u] = dep[f] + 1; dis[u] = dis[f] + l; fa[u] = f; sze[u] = 1; for(int e = adj[u]; e; e = nxt[e]){ int v = go[e]; if(v == f) continue; dfs1(v, u, len[e]); sze[u] += sze[v]; if(sze[v] > sze[son[u]]) son[u] = v; } } inline void dfs2(const int &u, const int &f){ if(son[u]){ //先查重儿子， 保证重链连续 top[son[u]] = top[u]; idx[pos[son[u]] = ++tot] = son[u]; dfs2(son[u], u); } for(int e = adj[u]; e; e = nxt[e]){ int v = go[e]; if(v == f || v == son[u]) continue; top[v] = v; idx[pos[v] = ++tot] = v; dfs2(v, u); } } inline int lca(int u, int v){ while(top[u] != top[v]){ if(dep[top[u]] < dep[top[v]]) swap(u, v); u = fa[top[u]]; } if(u == v) return u; if(dep[u] < dep[v]) return u; else return v; } int main(){ // freopen("h.in", "r", stdin); n = Re(), m = Re();; for(int i = 1; i < n; i++){ int a = Re(), b = Re(), c = Re(); addEdge(a, b, c); } dfs1(1, 0, 0); pos[1] = top[1] = idx[1] = tot = 1, dep[0] = -1; dfs2(1, 0); for(int i = 1; i <= m; i++){ int a = Re(), b = Re(); int L = lca(a, b); Wr(dis[a] + dis[b] - 2 * dis[L]), putchar('\n'); } return 0; }
【离线】
【tarjan】
奇妙的算法。但要求必须离线，先记录下所有的询问，再挨个找到答案。
用$dfs$的思想，现将子树扫描完，再返回根节点，进入下一颗子树。
tarjan求lca则每扫描完一颗子树，就将他与根节点的并查集进行合并，然后处理有关询问（可能现在还没法回答）。
如下图所示：比如我要查找$(4, 5), (4, 6)$的$lca$
扫描完$4$这颗子树后，4的并查集祖先已经设置为2，就可以开始尝试处理$4$中 的询问了
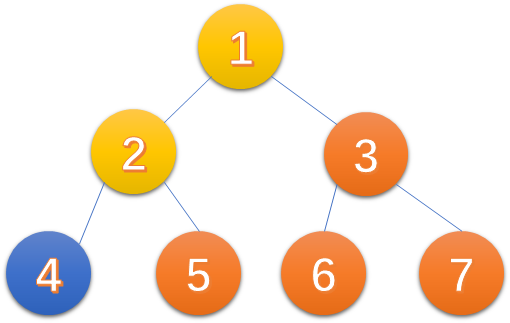
但是，处理4-6, 4-5询问时，发现5、6还没被访问到，所以回答失败，继续dfs。
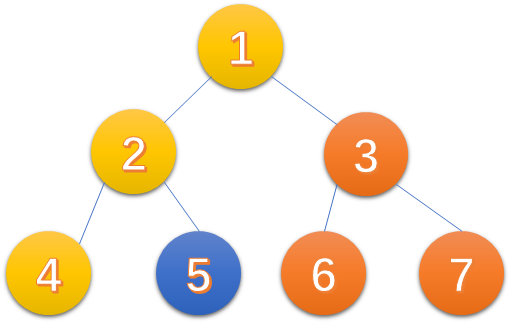
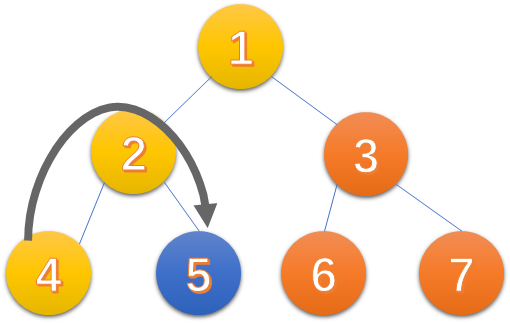
扫描完5，处理询问，发现4已经访问过，而我dfs时从4返回到2，4的并查集祖先已经设置为2，然后我跨过2到达5，所以4和5的祖先一定就是getAnc(4) = 2.
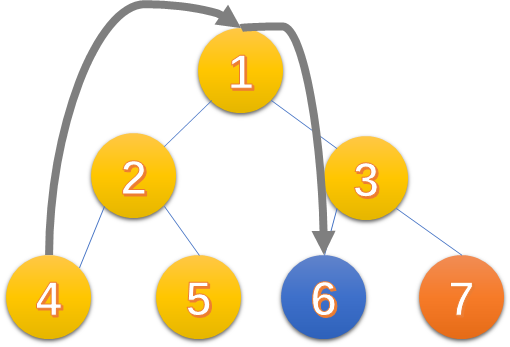4-6同理，,2的祖先被设置为1,那么4通过并查集的维护最终祖先也变为1，跨过1后到达6，那么4-6的lca一定为1.
看懂了这个算法，就明白为什么必须要求离线了。
【code】求两点lca
#include<iostream> #include<cstring> #include<string> #include<cstdio> #include<cstdlib> #include<algorithm> #include<vector> using namespace std; #define mp make_pair const int N = 100005; int ecnt, adj[N], go[N << 1], nxt[N << 1], len[N << 1]; int n, m, qa[N], qb[N], qans[N]; vector<pair<int, int> > vq[N]; int anc[N], dis[N]; bool vst[N]; int read(){ int i=0,f=1;char ch; for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar()); if(ch=='-') {f=-1;ch=getchar();} for(;ch>='0'&&ch<='9';ch=getchar()) i=(i<<3)+(i<<1)+(ch^48); return f*i; } inline void wr(int x){ if(x < 0) putchar('-'), x = -x; if(x > 9) wr(x / 10); putchar(x % 10 + '0'); } inline void addEdge(int u, int v, int l){ nxt[++ecnt] = adj[u], adj[u] = ecnt, go[ecnt] = v, len[ecnt] = l; nxt[++ecnt] = adj[v], adj[v] = ecnt, go[ecnt] = u, len[ecnt] = l; } inline int getAnc(int u){ return (u == anc[u]) ? u : (anc[u] = getAnc(anc[u])); } inline void Merge(int u, int v){ int fu = getAnc(u), fv = getAnc(v); if(fu != fv) anc[fu] = fv; } inline void tarjan(int u, int f, int d){ dis[u] = dis[f] + d; for(int i = adj[u]; i; i = nxt[i]){ if(go[i] == f) continue; if(!vst[go[i]]){ tarjan(go[i], u, len[i]); Merge(go[i], u); anc[getAnc(u)] = u; } } vst[u] = true; for(int i = 0; i < vq[u].size(); i++){ if(vst[vq[u][i].first]) qans[vq[u][i].second] = getAnc(vq[u][i].first); } } int main(){ n = read(), m = read(); for(int i = 1; i < n; i++){ int a, b, c; a = read(), b = read(), c = read(); addEdge(a, b, c); } for(int i = 1; i <= m; i++){ int u, v; u = read(), v = read(); qa[i] = u, qb[i] = v; vq[u].push_back(mp(v, i)), vq[v].push_back(mp(u, i)); } for(int i = 1; i <= n; i++) anc[i] = i; tarjan(1, 0, 0); for(int i = 1; i <= m; i++){ int ans = dis[qa[i]] + dis[qb[i]] - 2 * dis[qans[i]]; wr(ans), putchar('\n'); } return 0; }
