HDU6395-Sequence 矩阵快速幂+除法分块 矩阵快速幂模板

（有任何问题欢迎留言或私聊 && 欢迎交流讨论哦

Catalog

目录

• Catalog
  • Problem：Portal传送门
• Solution：
  • AC_Code：
  • Problem Description：
  • 模板：

Problem：Portal传送门

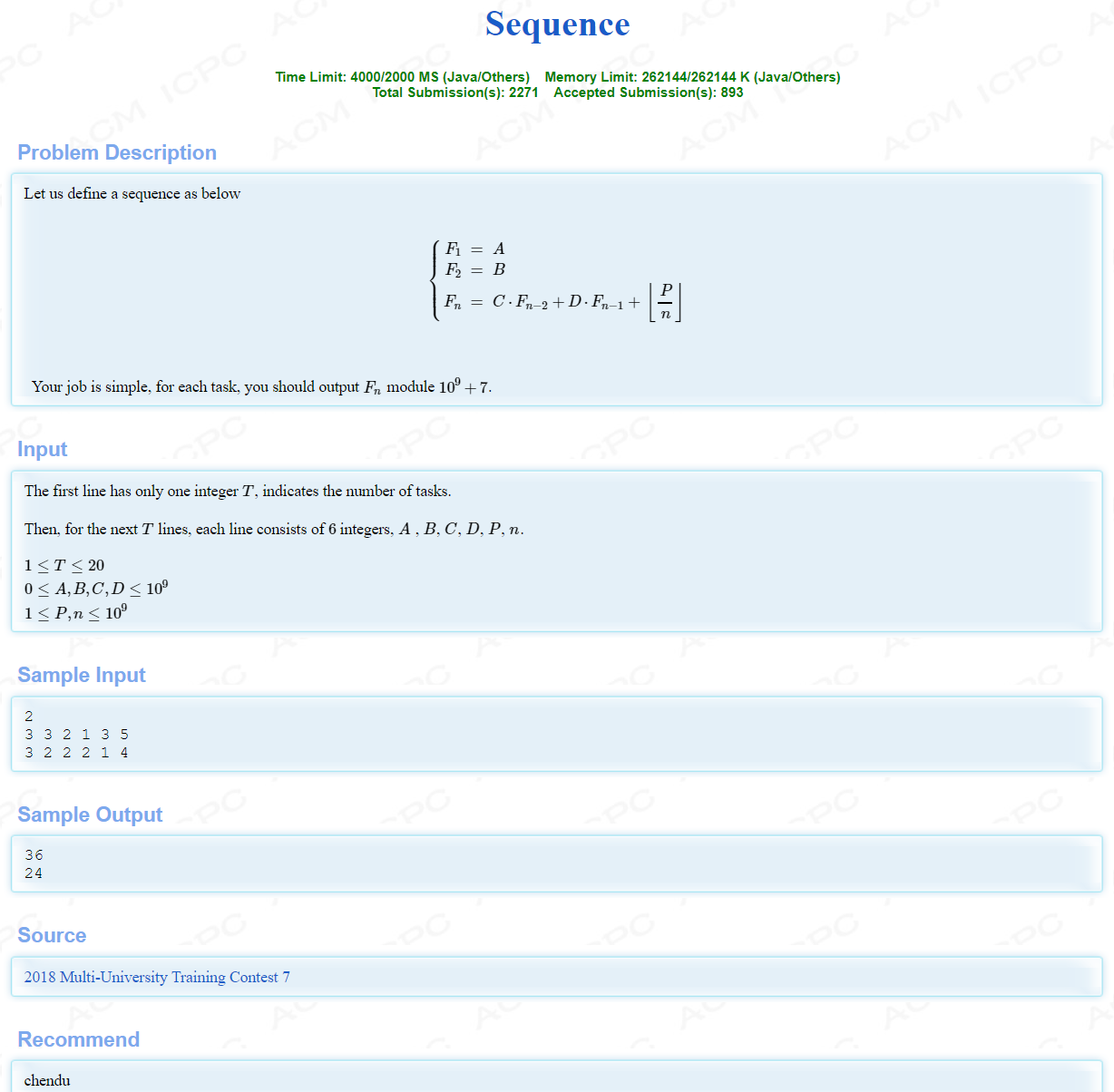
 原题目描述在最下面。

Solution：

 一看矩阵快速幂，再一看怎么多一个变项？\(⌊ \frac{p}{n}⌋\)？
 我去，\(⌊ \frac{p}{n}⌋\)这不是前几天写过的一道除法分块经典题吗？
 关于除法分块，请看这里：GYM101652
 然后，就没有然后了~

AC_Code：

#include<bits/stdc++.h>
#define mme(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const int MXN = 5e5+7;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
int n;
LL A,B,C,D,P;
struct lp{
  LL ar[3][3];
}aa, bb, cc;
lp exe(lp a,lp b,int n,int m,int h){
    lp c; memset(c.ar,0,sizeof(c.ar));
    for(int k = 0; k < m; ++k){
        for(int i = 0; i < n; ++i){
            if(a.ar[i][k] == 0) continue;
              for(int j = 0; j < h; ++j){
                if(b.ar[k][j] == 0) continue;
                c.ar[i][j] += a.ar[i][k] * b.ar[k][j];
                c.ar[i][j] %= MOD;
            }}}
    return c;
}
lp ksm(lp a, LL b, int n){
  lp ret;
  for(int i=0;i<n;++i) for(int j=0;j<n;++j) ret.ar[i][j]=(i==j);
  while(b>0){
    if(b&1) ret=exe(ret, a, n, n, n);
    a = exe(a, a, n, n, n); b >>= 1;
  }
  return ret;
}
int main(){
#ifndef ONLINE_JUDGE
    freopen("E://ADpan//in.in", "r", stdin);
    //freopen("E://ADpan//out.out", "w", stdout);  
#endif
  int tc = 0;
  int tim;
  scanf("%d", &tim);
  while(tim--){
    scanf("%lld%lld%lld%lld%lld%d", &A,&B,&C,&D,&P,&n);
    if(n == 1){
      printf("%lld\n", A);
      continue;
    }else if(n == 2){
      printf("%lld\n", B);
      continue;
    }else if(n == 3){
      printf("%lld\n", (B*D%MOD+A*C%MOD+P/3)%MOD);
      continue;
    }
    /*aa.ar[3][3] = {
      {D,1LL,0LL},
      {C,0LL,0LL},
      {xLL,0LL,1LL},
    };*/
    memset(aa.ar,0,sizeof(aa.ar));
    memset(bb.ar,0,sizeof(bb.ar));
    aa.ar[0][0]=D;
    aa.ar[1][0]=C;
    aa.ar[0][1]=1;
    aa.ar[2][2]=1;
    bb.ar[0][0]=B;
    bb.ar[0][1]=A;
    bb.ar[0][2]=1;
    /*bb.ar[3][3] = {
      {B,A,1},
    };*/

    //这是参考大佬的写法一
    for(LL l = 3, r; l <= n; l = r + 1){
      if(P/l) r = min(P/(P/l),n*1LL);
      else r = n;
      aa.ar[2][0] = P/l;
      cc = ksm(aa, r-l+1, 3);
      bb = exe(bb, cc, 3, 3, 3);
    }
    
    /*这是我本来繁琐的写法
    for(LL l = 3, r; l <= P; l = r + 1){
      r = min(P/(P/l),n*1LL);
      aa.ar[2][0] = P/l;
      cc = ksm(aa, r-l+1, 3);
      bb = exe(bb, cc, 3, 3, 3);
      if(r == n * 1LL)break;
    }
    if(P <= n - 1){
      LL m = n - (P+1)+1;
      aa.ar[2][0] = 0;
      if(P<3)m = n-2;
      cc = ksm(aa, m, 3);
      bb = exe(bb, cc, 3, 3, 3);
    }*/
    printf("%lld\n", bb.ar[0][0]);
  }
  return 0;
}

Problem Description：

模板：

typedef vector<long long> vec;
typedef vector<vec > mat;

mat Mul(mat a, mat b) {
    mat c(a.size(), vec(b[0].size()));
    for(int k = 0; k < b.size(); ++k) {
        for(int i = 0; i < a.size(); ++i) {
            if(a[i][k] == 0) continue;
            for(int j = 0; j < b[0].size(); ++j) {
                c[i][j] = (c[i][j] + a[i][k] * b[k][j])%mod;
            }
        }
    }
    return c;
}
mat mat_ksm(mat a, LL b) {
    mat res(a.size(), vec(a.size()));
    for(int i = 0; i < a.size(); ++i) res[i][i] = 1;
    while(b) {
        if(b&1) res = Mul(res, a);
        a = Mul(a, a);
        b >>= 1;
    }
    return res;
}
LL fib_n(LL n) {
    mat a(2, vec(2));
    a[0][0] = 1; a[0][1] = 1;
    a[1][0] = 1; a[1][1] = 0;
    a = mat_ksm(a, n);
    return a[1][0];
}