北京集训:20180323

T1:

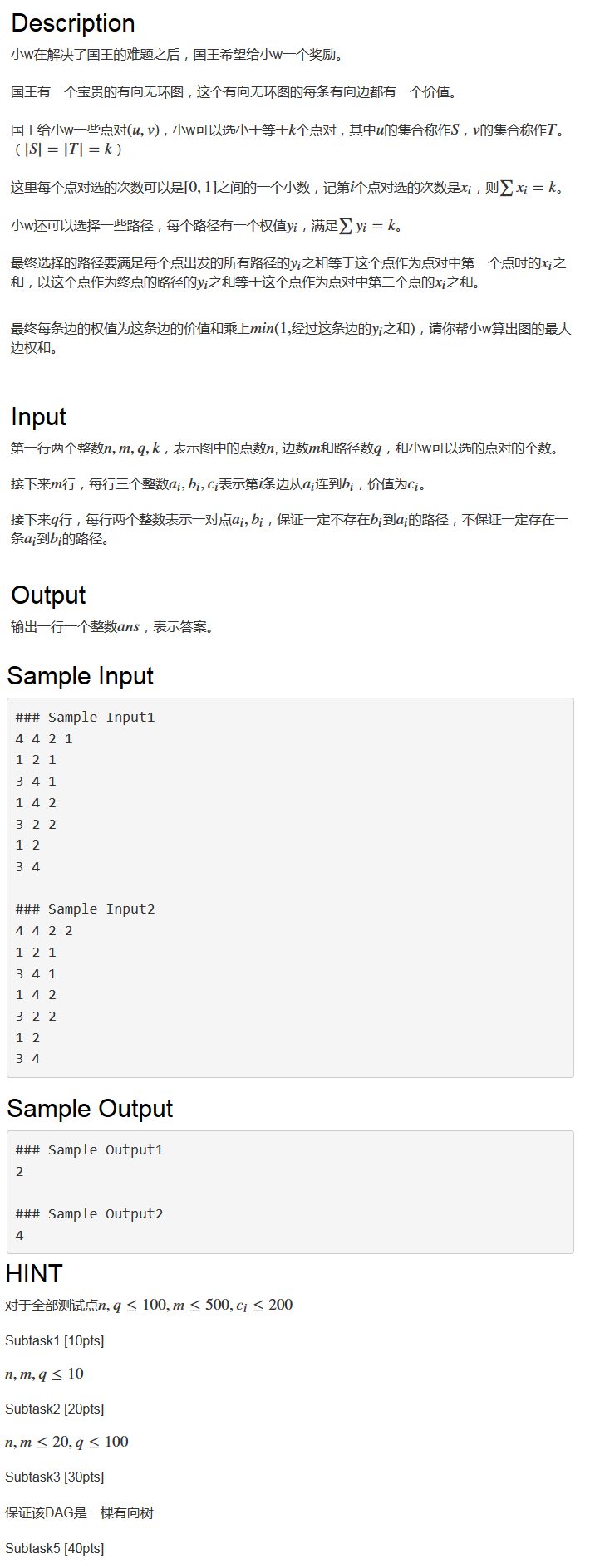
这题又是动态题面问题，一开始连求什么都没告诉你......
当时自然没有看了，现在没人做没人改......
官方题解:

标程:

#include <iostream>
#include <cstdio>
#include <map>
#include <set>
#include <queue>
#include <vector>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define dep(i,a,b) for(int i = a; i >= b; i--) 
#define Rep(i,a) for(int i = 0; i < a; i++)
#define pb(a) push_back(a)
#define mp(a,b) make_pair(a,b)
#define ab(x) ((x) < 0 ? -(x) : (x))
using namespace std;
typedef long long LL;
typedef map<int, int>::iterator mit;
typedef set<int>::iterator sit;
typedef pair<int, int> pii;
#define x first
#define y second
const int N = 1e5, E = 1e5, inf = 1e9;
int n, m, q, k, S, T, C[E << 1];
struct edge{ int to, pre, w, c; } e[E << 1]; int u[N], l = 1;//l==1!
void ins(int a, int b, int w, int c) { e[++l] = (edge){b, u[a], w, c}, u[a] = l; }
void insert(int a, int b, int w, int c) { ins(a, b, w, c), ins(b, a, 0, -c); }
#define v e[i].to
#define reg(i,a) for(int i = u[a]; i; i = e[i].pre)
#define ec e[i].c
#define ew e[i].w
int cost, h[N], c;
bool vis[N];
bool dij() {
    static pii q[E]; int l = 1;
    rep(i,S,T) h[i] = inf, vis[i] = false; q[1] = mp(-(h[S] = 0), S);
    while (l) {
        int x = q[1].y; pop_heap(q + 1, q + l + 1), l--;
        if (vis[x] || h[x] == inf) continue; vis[x] = true;
        reg(i,x) if (ew && h[x] + ec < h[v]) {
            h[v] = h[x] + ec; 
            q[++l] = mp(-h[v], v); push_heap(q + 1, q + l + 1);
        }
    }
    rep(x,S,T) reg(i,x) ec -= h[v] - h[x];
    c += h[T];
    return h[T] < inf;
}
int cur[N];
int dfs(int x, int f) {
    if (x == T) return f;
    int w, used = 0; vis[x] = true;
    for(int i = cur[x]; i; i = e[i].pre) if (ew && !ec && !vis[v] && ~h[v]) {
        w = min(ew, f - used), w = dfs(v, w);
        ew -= w; if (ew) cur[x] = i;
        e[i ^ 1].w += w;
        used += w; if (used == f) break;
    }
    vis[x] = false;
    if (!used) h[x] = -1;
    return used;
}
void flow() {
    while (dij()) { 
        rep(i,S,T) cur[i] = u[i], vis[i] = false;
        int w = dfs(S, inf);
        cost += c * w; 
    }
}
 
int ans = 0, d[N];
void addedge(int a, int b, int c) {
    ans += c;
    insert(a, b, q, 0); d[b]++, d[a]--; insert(b, a, 1, c * 100); 
}
int a[N], b[N];
map<int, int> f;
int check(int c1) {
    if (f.find(c1) != f.end()) return f[c1];
    static int u1[N], l1; 
    rep(i,S,T) u1[i] = u[i]; l1 = l;
    rep(i,1,l) C[i] = e[i].c;
    rep(i,1,q) insert(b[i], a[i], 1, c1 * 100 + 1);
    cost = c = 0; flow();   
    rep(i,S,T) u[i] = u1[i]; l = l1;
    rep(i,1,l) e[i].c = C[i];
    for(int i = 2; i <= l; i += 2) 
        e[i].w += e[i ^ 1].w, e[i ^ 1].w = 0;
    return f[c1] = cost;
}
 
void solve() {
    int l = -1, r = 1e5 + 10;
    while (l + 1 < r) {
        int mid = (l + r) >> 1;
        if (check(mid) % 100 <= k) r = mid; else l = mid; 
    }
    int C = check(r);
    ans = ans - C / 100 + r * k;
}
 
int main() {
    scanf("%d%d%d%d",&n,&m,&q,&k);
    S = 0, T = n + 1;
    rep(i,1,m) {
        int a, b, c; scanf("%d%d%d",&a,&b,&c);
        addedge(a, b, c);
    }
    rep(i,1,n) if (d[i] > 0) insert(S, i, d[i], 0); else if (d[i] < 0) insert(i, T, -d[i], 0);
    rep(i,1,q) scanf("%d%d",a + i, b + i);
    solve();
    printf("%d\n", ans);
    return 0;
}

T2:

多笔画问题，大概是什么网络流吧......
等等，这数据范围怎么流?
大概也会有部分分吧......
于是在想了几种算法都被下面的几种情况叉了后，弃疗了......

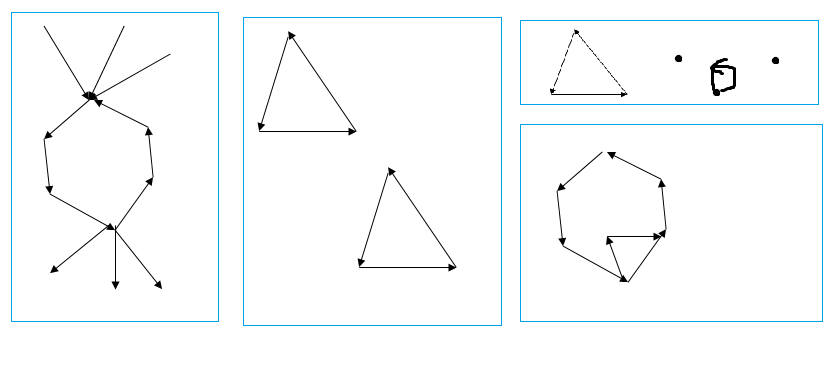
正解真的是费用流。
考虑如果只有有向图的话，答案为多出的总出度求和，也就是每个点度数的绝对值求和除以二。
关于这个结论为什么是正确的，考虑如果某个点的度数不为0的话，一定需要有一些路径从这个点起始或者在这个点终止。
有无向边怎么办?类比混合图欧拉回路问题，先给每个无向边钦定一个方向，然后连反转方向的单向边。
然后考虑每个点怎么向源点汇点连边。考虑当连接向某个点的一条边改变方向，这个点的度数会变化2。
如果一个点的度数为偶数，则直接向源汇连流量为度数除以二的边即可。
然而当一个点的度数为奇数，那么他的最后一次变化会存在1变-1或者-1变1的情况。
这时候这条边的方向改变在这个点上是不会产生价值的，但是可能对另一端的另一个点产生价值。
于是我们需要费用流，对能对这个点产生价值的边价值为1，不能对这个点产生价值的边价值为0。
(为什么混合图欧拉回路没有这个问题?因为如果度数为奇数则直接无解了......)
再次梳理一下我们的建图:为偶数则直接除以二连源汇，费用1，为奇数则除以二连源汇，费用1，最后加一条流量1费用0的边。
然而这样做会WA!看到上面的那张图了吗?他们就是最直接的反例!
因为可能有多个联通块，所以我们需要对联通块分别讨论。
对于没有边的单点联通块，对答案贡献为0。
对于自身形成欧拉回路的联通块，对答案贡献为1。
其余联通块我们的算法能正确处理。
这题数据有自环有独立点，这样分别处理就好了......
其实写的时候也没有这么麻烦，用并查集维护一下联通块，用数组维护一下联通块内有没有边，网络流跑完之后更新一下度数判断下有没有欧拉回路即可。
另外看到这题数据范围了吗?正常单路增广费用流铁定TLE，你需要多路增广费用流。
这又是什么呢?把dinic的bfs换成spfa，然后在增广的时候判定一下路径长度和下一步的点是否在栈中即可(否则长度为0的边可能会导致两个点无限递归)。
这道题告诉我们:有道理的特判能解决的反例都不是反例。
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>
#include<queue>
#include<vector>
#define debug cout
using namespace std;
const int maxn=1e4+1e2,maxe=5e4+1e2;
const int inf=0x3f3f3f3f;

int x[maxe],y[maxe],dir[maxe],mem[maxe];
int mrk[maxn],deg[maxn]; // deg :: in degree .
int n,m,ans;

namespace Flow {
    int s[maxn],t[maxe<<2],nxt[maxe<<2],f[maxe<<2],c[maxe<<2],cnt=1;
    int dis[maxn],inq[maxn],ins[maxn],st,ed;

    inline void coredge(int from,int to,int flow,int cost) {
        t[++cnt] = to , f[cnt] = flow , c[cnt] = cost ,
        nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void singledge(int from,int to,int flow,int cost) {
        coredge(from,to,flow,cost) , coredge(to,from,0,-cost);
    }
    inline bool spfa() {
        memset(dis+1,-1,sizeof(int)*ed) , dis[st] = 0;
        queue<int> q; q.push(st) , inq[st] = 1;
        while( q.size() ) {
            const int pos = q.front(); q.pop() , inq[pos] = 0;
            for(int at=s[pos];at;at=nxt[at]) {
                if( f[at] && dis[t[at]] < dis[pos] + c[at] ) {
                    dis[t[at]] = dis[pos] + c[at];
                    if( !inq[t[at]] ) q.push(t[at]) , inq[t[at]] = 1;
                }
            }
        }
        return dis[ed] > 0 ;
    }
    inline int dfs(int pos,int flow) {
        if( pos == ed ) return flow;
        ins[pos] = 1;
        int ret = 0 , now = 0;
        for(int at=s[pos];at;at=nxt[at]) if( f[at] && !ins[t[at]] && dis[t[at]] == dis[pos] + c[at] ) {
            now = dfs(t[at],min(flow,f[at]));
            ret += now , flow -= now ,
            f[at] -= now , f[at^1] += now;
            if( !flow ) {
                ins[pos] = 0;
                return ret;
            }
        }
        if( !ret ) dis[pos] = -1;
        ins[pos] = 0;
        return ret;
    }
    inline int flow() {
        int ret = 0;
        while( spfa() ) {
            ret += dis[ed] * dfs(st,inf);
        }
        return ret;
    }
}

struct UnionFindSet {
    int fa[maxn];
    inline int findfa(int x) {
        return fa[x] == x ? x : fa[x] = findfa(fa[x]);
    }
    inline void merge(int x,int y) {
        x = findfa(x) , y = findfa(y);
        mrk[fa[x]=y] = 1;
    }
    inline void init() {
        for(int i=1;i<=n;i++) fa[i] = i;
    }
}ufs;

inline void build() {
    using namespace Flow;
    st = n + 1 , ed = n + 2;
    for(int i=1;i<=n;i++) {
        if( deg[i] > 0 ) ans += deg[i];
        if( ! ( deg[i] & 1 ) ) {
            if( deg[i] > 0 ) singledge(st,i,deg[i]>>1,1);
            else if( deg[i] < 0 ) singledge(i,ed,(-deg[i])>>1,1);
        } else {
            if( deg[i] > 0 ) singledge(st,i,deg[i]>>1,1) , singledge(st,i,1,0);
            else singledge(i,ed,(-deg[i]>>1),1) , singledge(i,ed,1,0);
        }
    }
    for(int i=1;i<=m;i++) if( dir[i] ) singledge(y[i],x[i],1,0) , mem[i] = cnt - 1;
}
inline void initans() {
    static vector<int> vec[maxn];
    for(int i=1;i<=n;i++) vec[ufs.findfa(i)].push_back(i);
    for(int i=1;i<=m;i++) if( dir[i] && !Flow::f[mem[i]] ) deg[x[i]]+=2 , deg[y[i]]-=2;
    for(int i=1,fail;i<=n;i++) if( vec[i].size() ) {
        fail = 0;
        for(unsigned j=0;j<vec[i].size();j++) if( deg[vec[i][j]] ) {
            fail = 1;
            break;
        }
        if( mrk[i] && !fail ) ++ans;
    }
}

inline int getint() {
    int ret = 0 , ch;
    while( !isdigit(ch=getchar()) );
    do ret=ret*10+ch-'0'; while( isdigit(ch=getchar()) );
    return ret;
}

int main() {
    n = getint() , m = getint() , ufs.init();
    for(int i=1;i<=m;i++) {
        --deg[x[i]=getint()] , ++deg[y[i]=getint()] , dir[i] = getint();
        ufs.merge(x[i],y[i]) , mrk[ufs.findfa(x[i])] = 1;
    }
    build();
    ans -= Flow::flow() , initans();
    printf("%d\n",ans);
    return 0;
}

T3:

一看就没思路啊......
手玩一下发现 好像长度为2^k的边都有解，于是写了一个puts("ephemeral")骗分。
然而并不会证明QAQ(但是最后竟真的有分)。
说一下正解。
考虑区间长度为len，如果len=r*k，r为循环长度的话。
考虑把长为len的环按照i%r分类，如果i%r相同的每个灯取出来构成的k个长度为r的环，有一个环是endless那么整个就是endless(因为跳蚤们总能只转k的倍数)。
并且如果按照(i-1)/r分类，分成k段长度为r的，如果r是个循环节(也就是说每个小环相同)，那么只要小环是ephemeral的，整个环就一定是ephemeral的。
第一个结论并没有什么用途，但是第二个结论十分重要:
假设len=x*(2^k)，k为可行的最大整数，那么当且仅当这r段完全相同的时候才会有解。
为什么?显然这r段相同的时候一定有解(我们可以对这r段进行相同的操作，那么旋转相当于在一个循环节内进行，而一个循环节有解)，充分性得证。
对于必要性，如果有一段不同，那么这个环上最少有两种状态不同的段，并且这两种段全部点亮的操作序列是不同的(显然不同)。
于是如果对每一段进行相同的操作，则这两种段一定不会同时点亮。
如果进行不同的操作，我们可以通过旋转让最少两个针对某种段的操作不会作用到针对的段上(脑补一下旋转)，并且这会生成种类更多的段，于是必要性得证。
感性理解一下，我们现在为(ABB)，对应的操作为(XYY)，我们通过一次旋转，让最后的序列变成(A^Y)(B^Y)(B^X)，当前存在至少两种段，还可以继续操作。
于是我们得到了一种算法:对于长度为len的一段[l,r]，我们求出最大的k使得(2^k)|len，然后我们只需要判定[l,r-(2^k)]==[l+(2^k),r]即可。
对于这个判定的证明，自己在纸上画一下即理解充分性和必要性。
关于长度为(2^k)的段一定有解的证明，看官方题解吧......

这道题告诉我们:不要纠结证明，大(xia)胆(jb)猜结论能得到正解。
代码:

#include<cstdio>
typedef unsigned long long int ulli;
const int maxn=1e5+1e2;
const int base = 3;
 
char in[maxn];
ulli h[maxn],pows[maxn];
 
inline int lowbit(int x) {
    return x & -x;
}
inline ulli segment(int l,int r) {
    return h[r] - h[l-1] * pows[r-l+1];
}
 
int main() {
    static int n,q;
    scanf("%d%d%s",&n,&q,in+1) , *pows = 1;
    for(int i=1;i<=n;i++) h[i] = h[i-1] * base + in[i] - '0' + 1 , pows[i] = pows[i-1] * base;
    for(int i=1,l,r,len;i<=q;i++) {
        scanf("%d%d",&l,&r) , len = lowbit(r-l+1);
        puts(l==r||segment(l+len,r)==segment(l,r-len)?"ephemeral":"endless");
    }
    return 0;
}

 

话说我这几天被月影洗了脑，满脑子都是里面的剧情，简直失了智。
医生说这种病是没法治的。
于是放几张图吧......

 

 关于我为什么不能让背景不透明?

这CSS已经成精了你知道吗?

我这样写都不行......

<style type="text/css">
.box{
    background-color:white
    position:relative; 
    opacity:1.0; 
    filter:alpha(opacity=100);
    -moz-opacity:1.0
    width:auto; 
    height:auto; 
    z-index:0;
}
</style>

<div class="box">
    <p><img src="......" alt="" /></p>
</div>