插入排序补充
2011-09-12 17:16 Clingingboy 阅读(3073) 评论(1) 编辑 收藏 举报
- 直接插入排序
- 折半插入排序
- 二路插入排序
- 表排序
- 希尔排序
插入排序有许多的变种,所以讨论一下
以此贴为基础
http://www.cnblogs.com/Clingingboy/archive/2010/07/02/1770057.html
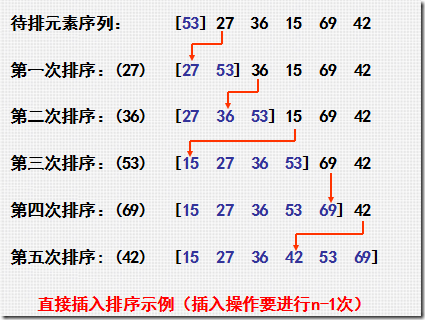
1.直接插入排序
如下图：
以顺序为主
插入排序主要做了2件事
- 寻找插入点
- 将所有插入点右侧元素向右移动
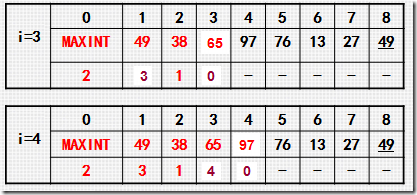
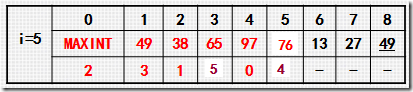
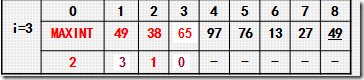
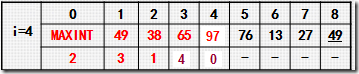
拿如上第二次排序举例:
寻找插入点可以有多种方法,如从头结点27开始找,或者从尾结点53开始找都是可以的.但是第2个步骤移动元素的动作是无法省略的.直接插入排序从尾结点边比较边移动元素,而并非等找到插入点后再移动元素.所以从尾结点开始向头结点找插入点则效率更好.
两种效率较低的做法
从左侧找插入点
//current sort value
int temp = arr[outer];
inner = 0;
//move range right
while (arr[inner] <= temp)
{
if (inner + 1 == arr.Length)
break;
inner++;
}
从右侧找插入点
int temp = arr[outer];
inner = outer;
//move range right
while (arr[inner - 1] >= temp)
{
inner--;
}
然后移动元素
if (inner < outer)
{
for (int j = outer; j > inner; j--)
{
arr[j] = arr[j - 1];
}
arr[inner] = temp;
}
以下则是边比较边移动,效率好些
public static void InsertionSort(this int[] arr)
{
int outer, inner;
//outer loop
for (outer = 1; outer < arr.Length; outer++)
{
arr.Display();
//current sort value
int temp = arr[outer];
inner = outer;
//move range right
while (inner > 0 && arr[inner - 1] >= temp)
{
arr[inner] = arr[inner - 1];
--inner;
}
arr[inner] = temp;
Console.Write(string.Format(" {0} swap with {1} ", arr[outer], temp));
arr.Display();
}
}
2.折半插入排序
改变了直接插入排序的第一个步骤,以折半查找的思想为基础,改善了找到插入点的速度,减少了比较的次数.但依然无法改变第2个步骤
public static void BInsertionSort(int[] arr)
{
int outer, inner;
//outer loop
for (outer = 1; outer < arr.Length; outer++)
{
//current sort value
int temp = arr[outer];
int low = 0, high = outer;
//compute current positon ready for insert
while (low <= high)
{
var mid = (low + high) / 2;
if (temp > arr[mid])
low = mid + 1;
else high = mid - 1;
}
//11,5
//low high
//move range right
for (int j = outer - 1; j > high; j--)
{
arr[j + 1] = arr[j];
}
//set current position value
arr[high + 1] = temp;
}
}
应该来说比较花不了多少时间，由于添加了折半查找反而添加了循环的次数
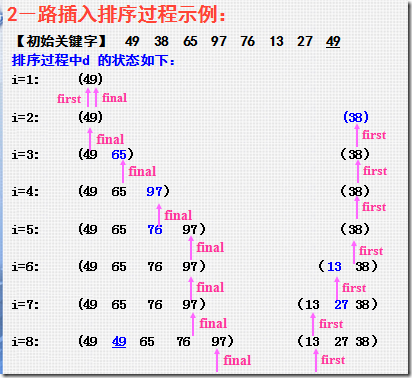
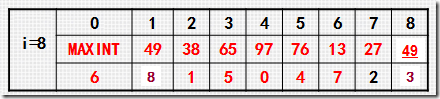
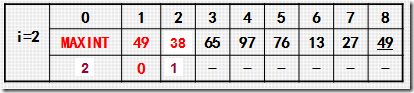
3.二路插入排序
为了减少移动元素的次数,需要一个辅助数组
final和first表示最后索引位置,注意命名：这里的first表示顺序表的第一个元素(最小值),final表示最后一个元素(最大值).因为其索引打乱了，即以第1个元素为准(枢纽),分成2路(左右两边,理解为2个有序的数组)进行插入排序,这样就减少了移动元素的次数
分以下情况:
- 待插入的元素大于最大值或小于最小值
- 最大值<x<最小值
其中第1种情况比较好解决
public static void Path2Insertion(int[] arr)
{
int length = arr.Length - 1;
int[] d = new int[length];
//flag index 1
d[0] = arr[1];
int final = 0, first = 0;
int inner = 0;
//index start from 2
for (int i = 2; i < arr.Length; i++)
{
inner = arr[i];
//miximum
if (inner < d[first])
{
first = (first - 1 + length) % length;
d[first] = inner;
}
//maximum
else if (inner > d[final])
{
d[++final] = inner;
}
}
}
上面两种情况同时更新了final和first的索引值和元素
现在考虑第2种情况,其又可以分两种情况讨论:
1.最大值<x<最小值(视其为一个索引值不以0开头的顺序表,即以first结尾,final开头)
这种比较并没有发挥 2路插入排序的优点,也并未减少移动的次数
int end = final;
while (inner < d[end])
{
//move right
d[(end + 1) % length] = d[end];
//minimum first
end = (end - 1 + length) % length;
}
//insert
d[end + 1] = inner;
//final++
final++;
2.细分最大值<x<最小值
d[0]<x<d[final] || d[first]<x<d[length-1]
这样的做法更能减少移动元素的次数.
所以2路排序选择关键字则非常重要，如果是枢纽是最小值或者是最大值则失去了意义.在移动程度上还是改善了移动的次数的
else if (final > 0 && inner < d[final] && inner >= d[0])
{
int end = final;
while (inner < d[end])
{
//move right
d[end + 1] = d[end];
//minimum first
end--;
}
//insert
d[end + 1] = inner;
//final++
final++;
}
else if (first > 0 && inner > d[first] && inner <= d[length - 1])
{
int end = length - 1;
while (inner < d[end])
{
//move left
d[first-1] = d[first];
//minimum first
end--;
}
//insert
d[end] = inner;
first--;
}
}
完整示例：
参考：http://www.cnblogs.com/wanggary/archive/2011/04/25/2028742.html
基于此修改
public static void Path2Insertion(int[] arr)
{
int length = arr.Length - 1;
int[] d = new int[length];
//flag index 1
d[0] = arr[1];
int final = 0, first = 0;
int inner = 0;
//index start from 2
for (int i = 2; i < arr.Length; i++)
{
inner = arr[i];
//miximum
if (inner < d[first])
{
first = (first - 1 + length) % length;
d[first] = inner;
}
//maximum
else if (inner > d[final])
{
d[++final] = inner;
}
else if (final > 0 && inner < d[final] && inner >= d[0])
{
int end = final;
while (inner < d[end])
{
//move right
d[end + 1] = d[end];
//minimum first
end--;
}
//insert
d[end + 1] = inner;
//final++
final++;
}
else if (first > 0 && inner > d[first] && inner <= d[length - 1])
{
int end = length - 1;
while (inner < d[end])
{
//move left
d[first-1] = d[first];
//minimum first
end--;
}
//insert
d[end] = inner;
first--;
}
}
for (int i = 1; i < arr.Length; i++)
{
arr[i] = d[(i + first - 1) % length];
}
}
4.表插入排序
先来理解一下概念,如下图
首先每个元素以三个变量来表示.数据结构定义如下
typedef struct
{
KeyType key; // key
InfoType otherinfo; //order
}RedType;
typedef struct
{
RedType rc;
int next; // next pointer
}SLNode;
typedef struct
{
SLNode r[SIZE];
int length;
}SLinkListType;
特征：
- 其是一个循环链表,第一个元素的值为最大值,其next永远指向最小值
最大值的next永远指向第一个元素(以形成循环链表) - 基于第1点的理解,当插入一个元素时,就需要更新之前值比该元素小的next
- 若遇到比自身值元素大的则更新自身的next
下图根据第3点
下图根据第2点
插入76,则需要同时更新65和76的next
实现：
初始化头结点
void TableInsert(SLinkListType *SL,RedType D[],int n)
{
int i,p,q;
//init firstNode
SLNode *firstNode=&SL->r[0];
firstNode->rc.key=INT_MAX;
firstNode->next=0;
SL->length=n;
}
插入结点情况:
- 插入最小值：更新头结点和自身结点next形成循环链表
for(i=0;i<n;i++)
{
//next node
SLNode *node=&SL->r[i+1];
node->rc=D[i];
q=0;
p=SL->r[0].next;
node->next=p;
SL->r[q].next=i+1;
SL->length=i+1;
}
2.插入一个最大值
q=0;
p=SL->r[0].next;
while(SL->r[p].rc.key<=node->rc.key)
{
q=p;
p=SL->r[p].next;
}
如下插入97,注意遍历是从第一个元素的next开始的
即38,49,65(按顺序遍历),q(3)指向前一个节点,p(0)指向查询节点的最后一个节点的next.
所以插入后更新如下
q的next为4(当前节点),4的next为p(前个节点)
完整示例:
void TableInsert(SLinkListType *SL,RedType D[],int n)
{
int i,p,q;
//init firstNode
SLNode *firstNode=&SL->r[0];
firstNode->rc.key=INT_MAX;
firstNode->next=0;
for(i=0;i<n;i++)
{
//next node
SLNode *node=&SL->r[i+1];
node->rc=D[i];
q=0;
p=SL->r[0].next;
while(SL->r[p].rc.key<=node->rc.key)
{
q=p;
p=SL->r[p].next;
}
node->next=p;
SL->r[q].next=i+1;
}
SL->length=n;
print(*SL);
printf("------------------------\n");
}
算法总结:更新插入节点的next值为前驱的next,更新前驱的next值为当前
插入节点的索引值.
根据以上规则,就可以得出表排序结果.又花了一些时间理解这么一小段代码,得出这么一句话的结论
http://wenku.baidu.com/view/30799f21bcd126fff7050bfc.html
http://wenku.baidu.com/view/6291e14c852458fb770b5642.html
http://wenku.baidu.com/view/c894023043323968011c9261.html
