[Codeforces] #436 E. Fire

E. Fire

time limit per test 2 seconds

memory limit per test 256 megabytes

input standard input

output standard output

 

Polycarp is in really serious trouble — his house is on fire! It's time to save the most valuable items. Polycarp estimated that it would taketi seconds to save i-th item. In addition, for each item, he estimated the value of di — the moment after which the item i will be completely burned and will no longer be valuable for him at all. In particular, if ti ≥ di, then i-th item cannot be saved.

Given the values pi for each of the items, find a set of items that Polycarp can save such that the total value of this items is maximum possible. Polycarp saves the items one after another. For example, if he takes item a first, and then item b, then the item a will be saved in ta seconds, and the item b — in ta + tb seconds after fire started.

Input

The first line contains a single integer n (1 ≤ n ≤ 100) — the number of items in Polycarp's house.

Each of the following n lines contains three integers ti, di, pi (1 ≤ ti ≤ 20, 1 ≤ di ≤ 2 000, 1 ≤ pi ≤ 20) — the time needed to save the item i, the time after which the item i will burn completely and the value of item i.

Output

In the first line print the maximum possible total value of the set of saved items. In the second line print one integer m — the number of items in the desired set. In the third line print m distinct integers — numbers of the saved items in the order Polycarp saves them. Items are 1-indexed in the same order in which they appear in the input. If there are several answers, print any of them.

Examples

input

3
3 7 4
2 6 5
3 7 6

output

11
2
2 3 

input

2
5 6 1
3 3 5

output

1
1
1 

Note

In the first example Polycarp will have time to save any two items, but in order to maximize the total value of the saved items, he must save the second and the third item. For example, he can firstly save the third item in 3 seconds, and then save the second item in another 2 seconds. Thus, the total value of the saved items will be 6 + 5 = 11.

In the second example Polycarp can save only the first item, since even if he immediately starts saving the second item, he can save it in3 seconds, but this item will already be completely burned by this time.

 

Analysis

背包问题= =（这数据暴露了啦！）

每一个物品有一个Deadline，超过Deadline这个物品就焚毁了（即无价值）

（其实我很好奇焚毁前一秒和焚毁时有什么区别吗 = = 改成Deadline时就蔓延到可能会更好）

除了这个额外的Deadline之外，剩下的就是背包的常规部分了

那么两层循环：

    for(int i = 1;i <= n;i++){
        for(int j = arr[i].d-1;j >= arr[i].t;j--){
            if(DP[j] < DP[j-arr[i].t]+arr[i].p){
                DP[j] = DP[j-arr[i].t]+arr[i].p;
            }
        }
    }

对于每一个物品，时间指针是从他的Deadline-1开始，逆向行走到营救所需时间结束

显然如果如果到了Deadline这个物品也是救不了的，因此 -1

但是根据问题我们还需要：最佳营救方案的营救物品数，最佳营救方案所营救到的物品列表

物品数，嗯，跟着DP[ j ]一起转移即可，物品列表可以在转移的时候登记前一个物品

于是乎

    for(int i = 1;i <= n;i++){
        for(int j = arr[i].d-1;j >= arr[i].t;j--){
            if(DP[j] < DP[j-arr[i].t]+arr[i].p){
                DP[j] = DP[j-arr[i].t]+arr[i].p;
                con[j] = con[j-arr[i].t]+1;
                last[j] = j-arr[i].t; // Means that: At i-Decide j-Item was chosen
                obj[j] = i;
            }
        }
    }

如此简单的码出来了=w=美滋滋

（ last 形似SPFA中记录最短路径的方式：只记录营救该物品时的前一个物品，也就是从状态转移过来的地方）

美滋滋地交上去，美滋滋地 Wrong Answer at Pretest 3

qwq

事实是这样：首先要根据Deadline排序

证明：正向证明-- 根据Deadline营救肯定是最优方案，从逻辑上来说这样是最正常的方式

　　　反向证明-- 已经码出来的背包DP从逻辑上来说，当前决策的 i 所继承的状态，是默认先救了那个被继承状态的物品然后再救 i 的，所以要根据Deadline排序才会是最优解

　　　最强证明-- 数据：物品A d=10 t=5 p=1，物品B d=5 t=1 p=1

（感谢CZL orz，CZL见我无法证明不排序的错误所在直接给了我这个数据，根据之前做法确实出了问题，但是我至今还是没法获得一个更优雅的证明qwq）

哪位大佬有更优雅的证明（不是拿数据去Hack qwq）欢迎留言qwq

真的急需qwq

排完序之后这部分DP就不会炸了，二维和一维都是一样的

那么接下来处理物品列表的问题

首先变路径数组 Last 为二维：

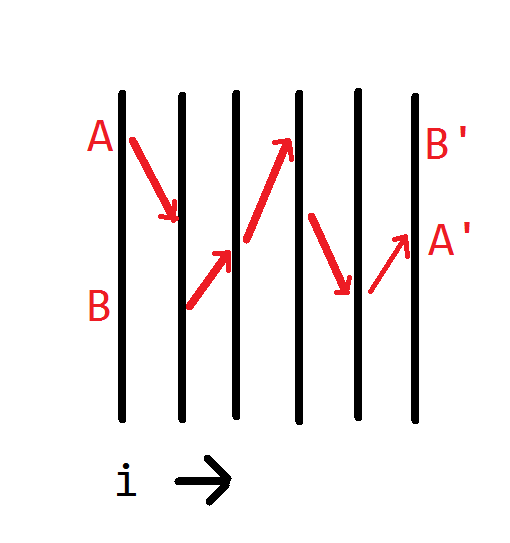
两个维都和背包一致，第一维 i 是决策的物品列表，第二维 j 是时间轴

那些红箭头表示当前状态是由上个物品决策的哪一次状态转移而来的

没有转移：那就是自己了

所以上图中有两条主要线路：A线和B线

A B为两条路线的起点，而A‘ B’为两条线路的终点

（思考思考 =w=）

那么如果开成我之前的一维，不难想象结果是一团糟

（事实上，因为某种原因，在检查Pretest 3的数据的时候，我发现我输出了5 5 5 5 5 5 5 5 7 7 7 7 7 ...）

将上述两个重点改进去后，总算是当晚补掉了E

= =不过难得会写E居然挂在背包上有点不甘

 

Code

#include<cstdio>
#include<algorithm>
#include<iostream>
#define maxn 3000
using namespace std;

int n,Poi,sPoi,con[maxn],last[maxn][maxn],obj[maxn],DP[maxn];
int stack[maxn],maxline;

struct item{
    int ord,d,t,p;
}arr[2000];

bool cmp(const item &a,const item &b){
    return a.d < b.d;
}

int main(){
    scanf("%d",&n);
    
    for(int i = 1;i <= n;i++){
        int d,t,p;
        scanf("%d%d%d",&t,&d,&p);
        arr[i].t = t;
        arr[i].d = d;
        maxline = max(maxline,d);
        arr[i].p = p;
        arr[i].ord = i;
    }
    
    sort(arr+1,arr+1+n,cmp);
    
    for(int i = 1;i <= n;i++){
//        for(int j = 1;j <= maxline;j++) last[i][j] = 0;
        for(int j = arr[i].d-1;j >= arr[i].t;j--){
            if(DP[j] < DP[j-arr[i].t]+arr[i].p){
                DP[j] = DP[j-arr[i].t]+arr[i].p;
                con[j] = con[j-arr[i].t]+1;
                last[i][j] = 1; // Means that: At i-Decide j-Item was chosen
                obj[j] = i;
            }
        }
    }
    
    int ans = -1,id = 0;
    for(int j = 0;j <= 2000;j++){
        if(ans<DP[j]){
            ans = DP[j];
            id = j;
        }
    }
    
    for(int i = n;i >= 1;i--){
        if(last[i][id]){
            id -= arr[i].t;
            stack[sPoi++] = arr[i].ord;
        }
    }
    
    printf("%d\n%d\n",ans,sPoi);
    
    for(int i = sPoi-1;i >= 0;i--) printf("%d ",stack[i]);
    
    return 0;
}