螺旋数组算法[上篇]--直接模拟算法

引子：

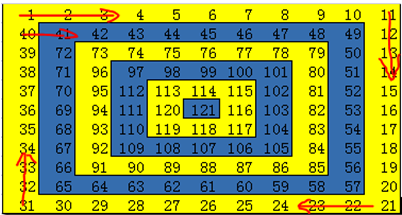
螺旋矩阵是一个比较经典的算法练习题。多数场景下要求练习者编写程序按螺旋方式填充一个边长为N (N>0) 的二维整形数组。如图

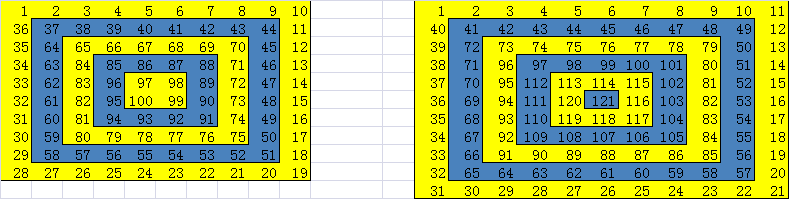
另外，还有的是将1至于螺旋中心，或者逆时针方向演进的。之所以今天发文讨论这个螺旋数组，主要有以下几点：

1、螺旋数组是一个经典习题

2、很多初级程序员至今没有找到理想的解。

由于缺乏正确的程序设计“世界观”，很多初级程序员无法独立探寻比单纯模拟更为巧妙地解，本系列也是为了总结一些常规的分析方法。

3、履行对园友的承诺

本人之前曾在园子里承诺过要发布一个能直接按坐标计算对应值的螺旋矩阵算法，结果迟迟没有成文。并且本人有一个解法至今在网上没有看见有相同或类似的解。因此发布一下，为广大算法爱好者做贡献。

4、为广大被面试的同学出口恶气

用螺旋数组做面试题，我听说过很多次。是不是在1小时内写不出来就是水平差呢？我感觉未必，我会用努力证明所有现有的算法都是有问题的，不优雅的。当你手握“标准”答案的时候，批评对方能力不足是太轻松的事情了。

场景简介

大多数的题目是这样的

常规思路

是人都知道这个螺旋矩阵里面是有规律的，但是这规律却也不是像打印星号直角三角形那么容易发现。

因此多数程序员都是采用“直接模拟算法”。

所谓直接模拟算法，就是很直白得把问题中提出的需求直接用代码方式模拟完成。

其实在多如牛毛的中小型项目中，用这种思路去实现客户需求的做法不说100%吧，95%是一定的。这是一个问题。

回到我们的这个需求，自然就是用一个大循环产生1到N平方的所有整数，然后在循环体内精确地判断矩形的四个边界，并调整实际的X，Y坐标，然后对目标数组的对应位置进行赋值

参考代码

以下代码收集自网络, 没有验证过

http://www.cppblog.com/issayandfaye/archive/2009/11/15/100976.html

#include<stdio.h>
#include<string.h>
#define MAX_SIZE 100
const  int  intx[]= {0,1,0,-1};
const  int  inty[]= {1,0,-1,0};
int  main()
{
    int  dir,i,j,n,data,x,y,nextx,nexty;
    int  arr[MAX_SIZE][MAX_SIZE];
    /**//*Read size*/
    printf("please input the size\n");
    scanf("%d",&n);
    /**//*Init*/
   x= y= 0;
   dir= 0;
   memset(arr,0,sizeof(arr));
    /**//*fill*/
    for(data=1; data<=n*n; data++)
   {
       arr[x][y]= data;
       nextx= x+intx[dir];
       nexty= y+inty[dir];
        if(arr[nextx][nexty] || nextx>=n || nexty>=n || nextx<0 || nexty<0)
       {
           dir++;
            if(dir==4)dir=0;
       }
       x+= intx[dir];
       y+= inty[dir];
   }
    for(i=0; i<n; i++)
   {
        for(j=0; j<n; j++)
            printf("%d\t",arr[i][j]);
        printf("\n");
   }
}

http://www.cnblogs.com/drizzlecrj/archive/2007/04/10/706784.html

void Simulate(int n)
{
    int x, y;
    x = y = (n - 1) / 2; //1的位置
    data[x][y] = 1;
    int len = 1;
    int count = 0;
    int num = 2;
    DIRECTION dir = RIGHT;
    while(num  <= n * n)
    {
        for(int i = 0; i < len; i++)
        {
            switch(dir)
            {
            case LEFT:
                --y;    break;
            case RIGHT:
                ++y;     break;
            case UP:
                --x;    break;
            case DOWN:
                ++x;    break;
            default:    break;
            }
            data[x][y] = num++;
        }
        count++;
        if(count == 2)
        {
            count = 0;
            len++;    
        }
        dir = (DIRECTION)((dir + 1) % 4);
    }
}
 

 

算法点评

直接模拟算法能解决很多问题,写起来还特别快速.

优点

算法思想直观, 实现简单, 在成功精确控制边界变量时很有成就感。

缺点

由于对目标数组的访问不是线性的, 在50%的情况下是跨行访问, 在数组尺寸较大时会出现细微性能问题。这个可以参考老赵的文章

计算机体系结构与程序性能 。我就是从那里学来的。

 

但是

从园友　农夫三拳 2007年的文章 面试题-螺旋矩阵(模拟) 中我们就已经可以发现其实可以找到一定的数学规律，因此下一篇我们开始讨论究竟有多少隐藏的意义在这个螺旋数组当中。

本篇总结

以下是个人牢骚，时间宝贵或不愿意听牢骚的情直接无视。

直接模拟算法，是我们广大程序员最熟悉的码代码的模式。而且它的确能胜任很多工作场合。错不在这个模式，在于我们的思维模式。

当思维模式成为思维定式，框死了我们的思想，从而感觉这个世界就是这样的，编码就是如此的，老子已经有5年编码经验了，老鸟了…..

那么，不幸的是，我们已经失去进步的机会了。

有很多事情我们不敢做，要么没时间做，但是如果连想都不敢想，甚至从来没主动尝试去想。

那么，没有自主思想的人，就是机器人，难听点的是僵尸。

 

导读：

螺旋数组算法[上篇]--直接模拟算法

螺旋数组算法[中篇]--常规数学分析

螺旋数组算法[下篇]--努力接近需求的本质 预计12/23日发布