《算法导论》第四章练习题 Exercise

4.1-1

　　通过分析知由于 FIND-MAX-CROSSING-SUBARRAY 返回的是数组A最中间的两个负数组成的数组，则经过分治算法 FIND-MAXIMUM-SUBARRAY 处理后，返回的是一个长度为1的只含最大负数的数组。

4.1-2

　　伪代码如下：

//Brute force to find max subArray
findMaxSubArray (A, low, high)
    max = -INF 
    for i = low to high
        sum = 0
        for j = i+1 to high
            sum = sum + A[j]
            if sum > max
                max = sum
                maxRight = i
                maxLeft = j

    return (max, maxRight, maxLeft) //return max subArray

4.1-3

　　性能交叉点要根据具体而定，大概在长度为 20 的数组时候可以发现此后递归算法的时间要明显低于暴力算法。

　　修改基本情况——当规模小于n₀时采用暴力算法可以优化递归算法的运行时间，性能交叉点不会发生变化。

4.1-4

　　允许结果返回空子数组的原因可能有二：1、该时期股票价格不变，无需买股票 2.该时期股票持续下跌，不买股票。

　　在 FIND-MAXIMUM-SUBARRAY 7～11行的语句中，增加判断：如果三个 sum 值中最大值的是 0 或者负数，那么返回空数组，即代表该时期股票价格保持不变甚至持续下跌，不买股票。更巧妙的方法是在执行该算法时先进行一次线性扫描，如果没有一个正数存在，说明股票没有增长，那么就返回空数组，代表该时期不买股票。

4.1-5

　　感觉这个算法是基于DP的思想，当前状态是由前面某一个阶段的状态转移决定的，子问题并不互相独立，也就是题目中说的：A[1..n+1] 的最大子数组要么是 A[1..n] 的最大子数组，要么是某一子数组 A[i..n+1] （ 1 <= i <= n+1）。

　　其实最大子数组问题等价于”最大连续和“ 问题，只不过还要把数组的右左索引记录下来，才可以得到一个数组。所以我们现在先把目标转到如何用DP求出最大连续和。

　　如何求出 A[1..i] 的最大连续和？分析知，A[1..i] 的最大连续和要么是 A[1..i-1] 的最大连续和加上 A[i]，要么就是 A[i] 。那么，设 b[i] 为最后一个元素是 A[i] 的数组的最大连续和，有 b[i] = max(b[i-1] + A[i], A[i]) ，看得出来，如果想要满足 b[i-1] + A[i] > A[i] ，那么就要满足 b[i-1] > 0 。

　　可以看得出来，这里影响下一步决策的因素就是 b[i] ，我们把它叫做状态。

　　举个例子，现有一数组 A = <-23, 18, 20, -7, 12, -5, -22> ，设最大连续和问题为状态，即 dp[i] 表示最后一个元素是A[i] 的数组的最大连续和，则有如下推导：

- dp[1] = A[1] = -23 (边界条件，只有一个元素的数组的连续最大和就等于该元素)
- dp[2] = max( dp[1] + A[2], A[2] ) = 18 (递归定义最优解 dp 的值)
- dp[3] = max( dp[2] + A[3], A[3] ) = 38
- dp[4] = max( dp[3] + A[4], A[4] ) = 31
- dp[5] = max( dp[4] + A[5], A[5] ) = 43
- dp[6] = max( dp[5] + A[6], A[6] ) = 38
- dp[7] = max( dp[6] + A[7], A[7] ) = 16
- ...
- dp[i] = max( dp[i-1] + A[i], A[i] ) (状态转移方程)

　　通过状态转移方程，我们可以得到数组 A[1..i] 的所有子数组的最大连续和。但是实际的编程中我们只需要存储所有最大连续和中的最大值，就不用数组存储了，用变量就足够了。

　　求最大连续和算法的伪代码如下：

maxSeqSum (A)
    dp = A[1]        //存储最大连续和，A[1] 本身就是 i =1 时的最大连续和
    res = A[1]        //存储所有子数组最大连续和的最大值
    for i = 2 to A.length           
        if dp > 0        //对应 " dp[i-1] + A[i] > A[i] ” 的情况
            dp += A[i] 
        else              //对应 “ dp[i] + A[i] <= A[i] ”的情况
            dp = A[i]
        if dp > res
             res = dp
    return res

　　这个时候，只要再计算索引，就可以解出 A 的最大子数组。计算索引的方法就很简单了，设 start、end 分别是最大子数组的左边界索引、右边界索引，每次需要缩短最大连续和数组为 A[i] 时就更新左边界为 i ，每次将A[i]添加到最大子数组的时候就更新右边界。需要注意的是求最大连续和的时候，扩充的元素不一定会添加到最大子数组里。

　　求最大子数组算法的伪代码如下：

findMaxSubarray (A)
    dp = A[1]
    res = A[1]
    start = end = 1
    for i = 2 to A.length
        if dp > 0
            dp += A[i]
        else
            dp = A[i]
            start = i
        if dp > res
            res = dp
            end = i
    return (start, end, res)

　　感觉 DP 确实很强，就这道题而言它比分治策略利用到更多的旧信息。　　

4.2-1

　　A11 = [1] ，A12 = [3] ，

　　A21 = [7] ，A22 = [5] 。

　　B11 = [6] ，B12 = [8]，

　　B21 = [4] ，B22 = [2]。

　　S1 = B12 - B22 = [6]，

　　S2 = A11 + A12 = [4]，

　　S3 = A21 + A22 = [12]，

　　S4 = B21 - B11 = [-2]，

　　S5 = A11 + A22 = [6]，

　　S6 = B11 + B22 = [8]，

　　S7 = A12 - A22 = [-2]，

　　S8 = B21 + B22 = [6]，

　　S9 = A11 - A21 = [-6]，

　　S10 = B11 + B12 = [14] 。　　

　　P1 = A11 • S1 = [6]，

　　P2 = S2 • B22 = [8]，

　　P3 = S3 • B11 = [72]，

　　P4 = A22 • S4 = [-10]，

　　P5 = S5 • S6 = [48]，

　　P6 = S7 • S8 = [-12]，

　　P7 = S9 • S10 = [-84]。

　　C11 = P5 + P4 - P2 + P6 = [18]，

　　C12 = P1 + P2 = [14]，

　　C21 = P3 + P4 = [62]，

　　C22 = P5 + P1 - P3 - P7 = [66]，

　　所以，

4.2-2

　　Strassen 算法的伪代码如下：

square-Matrix-Strassen (A, B)
    n = A.row     
    let C be a new n*n matrix
    if n == 1 //base case
        C11 = A11 • B11
    else //recursive case
        partition A, B, and C as in equations 4.9
        let S1, S2, S3, S4, S5, S6, S7, S8, S9, S10 be new n/2 * n/2 matrixs
        S1 = B12 - B22
        S2 =  A11 + A12
        S3 = A21 + A22
        S4 = B21 - B11
        S5 = A11 + A22
        S6 = B11 + B22
        S7 = A12 - A22
        S8 = B21 + B22
        S9 = A11 - A21
        S10 = B11 + B12
        P1 = square-Matrix-Strassen (A11, S1)
        P2 =  square-Matrix-Strassen (S2, B22)
        P3 =  square-Matrix-Strassen (S3, B11)
        P4 =  square-Matrix-Strassen (A22, S4)
        P5 =  square-Matrix-Strassen (S5, S6)
        P6 =  square-Matrix-Strassen (S7, S8)
        P7 =  square-Matrix-Strassen (S9, S10)
    C11 = P5 + P4 - P2 + P6
    C12 = P1 + P2
    C21 = P3 + P4
    C22 = P5 + P1 - P3 - P7
    return C

4.2-3

　　如果矩阵规模 n 不是 2的幂的情况，那就填充 0 使之成为方阵。填充的时间主要花费在复制上，最多 O(n2) ，所以算法的运行时间还是 Θ(n^lg7)　　　　

4.2-4

4.2-5

4.2-6

4.2-7

4.3-1

　　先吐槽一下，T(n) = T(n-1) + n，这不是插入排序（递归)的执行时间么，又在这见到了。

　　猜测：T(n) <= c · n²

　　证明：T(n) = T(n-1) + n <= c · (n-1)² + n = c · n² + (1-c) · n + (1-n) <= c · n² ，其中只要 c >= 1 、n >= 1 最后一步推导就成立。

　　所以 T(n) = T(n-1) + n = O(n²)

4.3-2

　　T(n) = T(⌈n/2⌉) + 1 ，这应该是二分查找（递归）的执行时间。

　　猜测：T(n) <= c · lgn

　　证明：n = 1 为递归式的基本情况，T(1) = 1。n >= 2 时， T(n) = T(⌈n/2⌉) + 1 <= c · lg(n/2) + 1 = c · lgn - c + 1 <= c · lgn ，其中只要 c >= 1 ，最后一步推导就会成立。　　

　　所以 T(n) = T(⌈n/2⌉) + 1 = O( lgn )　

4.3-3

　　猜测：T(n) >= c · n · lgn

　　证明：n = 1 为递归式基本情况，T(1) = 2T(⌊n/2⌋) + n = 1 。当 n >= 2 时，有 T(n) = 2T(⌊n/2⌋) + n >= 2 · c · ( ⌊n/2⌋ · lg⌊n/2⌋ ) + n >= ？，我的思路到这就卡着了，因为向下取整的符号会让左边 <= 右边，让接下去的推导无法成立，。如果这里是向上取整的符号的话，就可以推出 2 · c · ( ⌈n/2⌉ · lg⌈n/2⌉ ) + n >= c · n · (lgn - 1)+ n = c · n · lgn 。

　　看来是要换猜想了。加上些常数如何？

　　参考了别人的解法，新猜测：

　　证明：还是一样，n = 1 为递归式的基本情况，T(1) = 2T(⌊n/2⌋) + n = 1 。当 n >= 2 时，T(n) = 2T(⌊n/2⌋) + n >= 2c · ((⌊n/2⌋ + 2) · (lg⌊n/2⌋ + 2) + n >= 2c · ((n/2 - 1 + 2) · (lg(n/2) - 1 + 2) + n = 2c · ((n/2 + 1) · lgn) + n = c · (n + 2) · lgn + n >= c · n · lgn ，其中存在 c > 0，使得最后一步推导成立

　　所以 T(n) = Ω( n·lgn )

4.3-4

　　我前面的两道题都不对 n=1 进行归纳证明，而是把它们视为递归式中的基本情况而不是归纳证明的基本情况，即把 n=1 视为 ”边界条件“。然而可以通过做出不同的归纳假设，可以对边界条件进行归纳。下面是对 T(n) = 2T(⌊n/2⌋) + n 重新做出归纳，把边界条件 n = 1 包含到归纳证明里。

　　猜测：T(n) <= c · n·lgn + n 。n 是一个低阶项，不影响渐进解。

　　证明：T(n) = 2T(⌊n/2⌋) + n <= 2 · (c ·⌊n/2⌋ · lg⌊n/2⌋ + ⌊n/2⌋) + n <= 2 · (c · n/2 · lg(n/2) + n/2) + n = c · n · lgn + (2-c) · n <= c · n · lgn + n ，当 c >= 1 推导成立。

　　由 T(1) = 1 = c · 1 · lg1 + 1 = 1，可知边界条件 n =1 时归纳证明也成立。

4.3-5

　　”严格递归式“的意思是要对归并排序的奇偶输入进行区分，并非都为 T(n) = 2T(⌊n/2⌋) + n ，而是 T(n) = T(⌊n/2⌋) + T(⌈n/2⌉) + n 。

　　证明方法和 4.3-3 很类似，这就直接贴图了：

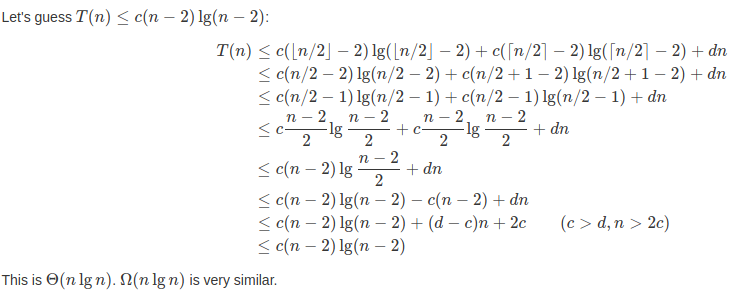
4.3-6

　　猜想：T(n) <= c · (n - a) · lg(n-a)

　　证明：T(n) = 2T(⌊n/2⌋ + 17) + n <= 2c · (⌊n/2⌋ + 17 - a) · lg(⌊n/2⌋ + 17 - a) + n <= 2c · (n/2 + 17 - a) · lg(n/2 + 17 - a) + n = c · (n + 34 - 2a) · lg((n + 34 - 2a)/2) + n = c · (n + 34 - 2a) · lg((n + 34 - 2a) - c · (n + 34 - 2a) + n <= c · (n + 34 - 2a) · lg((n + 34 - 2a) <= c · (n - a) · lg(n-a)

　　当 c > 1 、a >= 34 、n > n₀ = f(a) 时，才有后三步的推导。

　　所以 T(n) = 2T(⌊n/2⌋ + 17) + n = O(n · lgn)

　　也就是说，在递归式 T 的参数中增减一个常数，对递归式的解影响不大。

4.3-7

　　猜想：

　　证明：

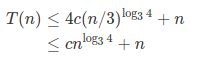
　　之后就无法缩放成猜想的形式了，gg。

　　再次猜想，这次减去一个低阶项：

　　证明：

　　再缩放一步就是我们想要的形式：

4.3-8

　　猜想：T(n) <= cn²

　　证明：T(n) = 4T(n/2) + n <= 4c · (n/2)² + n = c·n²+ n

　　凉了，存在多余的 n 且没法通过缩放而删除。

　　减去一个低阶项，再猜想T(n) <= cn² - n

　　证明：T(n) = 4T(n/2) + n <= 4 · (c(n/2)² - n/2) + n = cn²- n <= cn²

　　得到 T(n) = 4T(n/2) + n 的解为 Θ(n^2)　　

4.3-9

　　偷了点懒，过程借用书上改变变量的例题与主定理。

　　设 m = lgn ，由例题可知，T(2^m) = 3T(2^m/2) + m

　　记 S(m) = T(2^m) ，得 S(m) = 3S(m/2) + m

　　通过主定理，该情况对应 case 1 ，有 S(m) = Θ(m^lg3)

　　从 S(m) 转换成 T(n) ，得 T(n) = T(2^m) = S(m) = Θ(m^lg3) = Θ(lg^lg3n)

4.4-1

　　画出递归树，如下图：

　　树的深度 = lgn ，每层有 3ⁱ 个结点，i = lgn 。最底层有 3^lgn 个结点，其代价为 n^lg3 · T(1) = Θ(n^lg3) 。

　　接下来就是计算每层代价之和，这步比较简单，唯一的坑点就是得到的数列的指数是大于 1 的，不能用无穷等比级数公式对其进行简化得到上界，推导的时候可能稍微慢了一些。

　　该递归树得到渐进上界的推导过程：

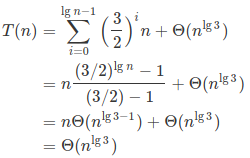
　　代入法还是比较坑，我先拿了 T(n) <= n^lg3 作为猜想去证明，但是多了一个 n ，gg。那么就换猜想，猜想是：(n) <= n^lg3- n 。接下来就小菜一碟了，很简单的证明过程，不贴了。

4.4-2

　　本题的递归树如下：

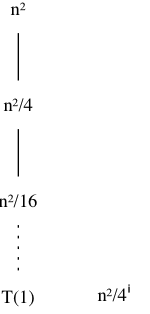
　　树的深度 lgn ，叶子结点有 1 个，叶子结点总代价为 (1/4)^lgn·c·n²，递归树总代价很容易求，这里直接贴图了：

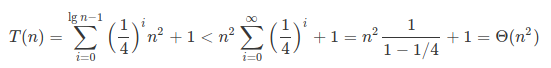
　　接下来用代入法验证，猜想为 T(n) <= cn²，一发入魂。证明很简单，如下：

4.4-3

　　这题可以猜的出来 T(n) = O(n^2) ，因为之前证明过递归式 T(n) = 2T(n/2) + n 中 T 的参数增减一个常量，它对执行时间没有显著影响。然后就可以当作普通的 T(n) = 4T(n/2) + n 去解，为 O(n2) 。

　　如果想更严谨一点，考虑常量的话，那么先画出递归树，注意递归式 T(n/2 + 2) 的意思是每次分解成规模为 n/2 + 2 的子问题。画出递归树如下：

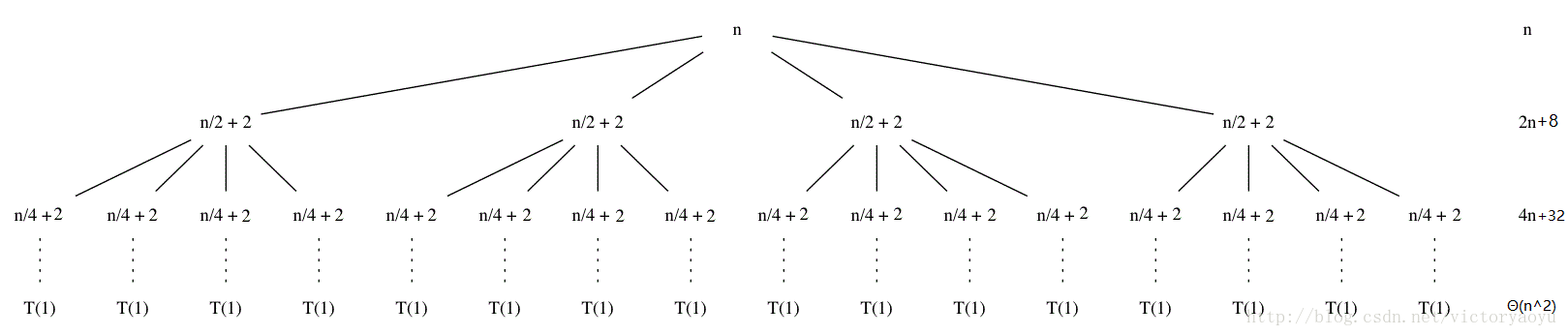
　　把 T(n) 看成两个数列求和，前一个数列 n, 2n, 4n ...很好解决，但是后一个数列 8, 32 .... 的关系还不会很明显，最好再画出第四层并计算这一层的时间代价。第四层是 128，为了计算方便，让深度 0, 1, 2, 3 ... lgn - 1, lgn ，对应 0, 8, 32, 128 ... 2^2lgn-1, 2^2lgn+1，和式为（由于最后一层叶子结点用于判断上界，这里先不计叶子结点那一层），求和要用到等比数列求和，高中的公式不能忘。

　　计算叶子结点那一层的代价:

　　所以总代价如下，很好求和的，这里我懒就不细写了：

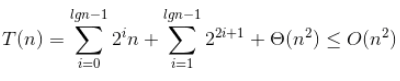
　　用代入法验证：

　　　　Guess:

　　　　　　T(n) <= cn^2 - an , a > 0

　　　　Prove:

　　　　　　T(n) = T(n/2 + 2) + n

　　　　　　　 <= c(n/2 + 2)² - (a/2 - 1)n - 2a = c/4 · n2 - (a/2 - 1 - 2c)n + 4c - 2a　　　　　　　　

　　　　　　　　<= c/4 · n²(a > 4c + 1, c> 0)

　　　　　　　　= Θ(n²)

4.4-4

　　这道题对中英文版会有差别，我书上的递归式是 T(n) = T(n-1) + 1 （中文版），而英文版的是T(n) = 2T(n-1) + 1。

　　递归树的形式和 4.4-2 一样，是一条线。每一层的代价都是 c ，共递归 n-1 次，所以很容易得到 T(n) = O(n)

　　代入法：

　　　　Guess: T(n) <= cn

　　　　prove: T(n) = T(n-1) + 1 <= cn -c + 1 <= n ，当 c >= 1 时最后一步推导成立。

4.4-5

　　种缺失结点的递归树只能得到一个不精确的上界。

　　把递归树的图画出来，取两种极端情况，一种是树高为 lgn ，此时上界应该是 O(n^2) ；一种树高是 n-1 ，此时上界应该是 O(2ⁿ) 。取更大的上界当作是本题的上界，并用代入法证明：

　　　　　Gress: T(n) <= c·2ⁿ - n

　　　　　Prove: T(n) = T(n-1) + T(n/2) + n <= c · 2^n-1 - c· (n+1) - c · n/2 + c · 2^n/2 + n <= c2ⁿ - c·n/2 <= c · 2ⁿ ，当 c>=1 且 n 足够大时最后两步推导成立

4.4-6

　　递归树的图就是书上的图 P4-6。

　　如果想得到下界，那么得找到最短路径，然后剪去最短路径终点那一层下方所有的枝，此时通过第一层的根结点到叶子结点之间的时间的总代价就是下界。

　　最短路径也很好找到，就是最左边不断地把 n 化为 n/3 的那一条路径。此时，树的深度为 log₃n ，叶子结点的数量是 2^log₃n ，每个叶子结点花费的时间代价是常数，且此时的树是完全二叉树，所以每一层时间代价都是 cn ，则有 T(n) = Ω(log₃n · n) ，由于在这里 log₃n 严格大于 log₂n，所以又有 T(n) = Ω(n·lgn)

4.4-7

4.4-8

4.4-9

4.5-1

　　a. T(n) = Θ(n^log₄2) = Θ(n^(1/2))

　　b. T= Θ(lgn · n^log₄2) = Θ(lgn · n^(1/2))

　　c. T(n) = Θ(n)

　　d. T(n) = Θ(n^2)

4.5-2

　　log₄a < log₂7 ，意味着 a < 49 （ log2 相当于开根号，解 log4 相当于开两次根号），所以 a 的最大整数是 48

4.5-3

　　n^log_ba = 1 ，f(n) = Θ(1) ，有 T(n) = Θ(n^log_ba· lgn) = Θ(lgn)

4.5-4

　　不可以，不是多项式大于。

　　画出递归树，根结点的时间代价为 n² · lgn ，其叶子结点的时间代价为 Θ(n^2) 。发现得到的和式很不好化简，但是很容易 Guess: T(n) = O(n² · lgn) ，那么就用代入法咯。

　　之后就是证明的过程了：

4.5-5

　　挺多的，但是我自己脑洞不够大，没想出来具体的。

4.6-1

4.6-2

4.6-3

　　...

posted @ 2018-01-20 12:58 bw98 阅读(1597) 评论(0) 编辑收藏举报

刷新页面返回顶部

大峰子的博客

实践你的热爱

《算法导论》第四章练习题 Exercise

大峰子的博客

实践你的热爱

《算法导论》第四章 练习题 Exercise

《算法导论》第四章练习题 Exercise