查找二叉树(插入、删除、查找)实现
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
如图:
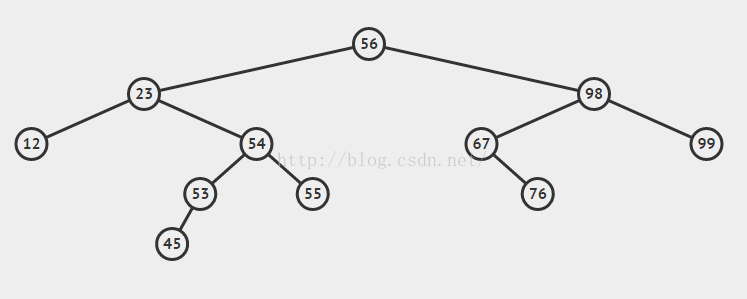
基于这样的特性,查找的时候就很好操作了,从根节点开始,查找,如果值大于节点值,往右找;如果值小于节点值,往左找;如果值刚好相等,就找到了。是不是看着就能写出代码了?这种查找过程很像二分查找法,但是那个是数组结构,这个是树结构。
二叉查找树的操作基本概括为:插入值,删除值,查找值以及二叉树的遍历。
注意的是:这里面,删除是最麻烦的。
(本来觉得写数据结构还是用c语言最好的,直接可以操作指针,清晰明了效率高,但是c确实丢了太久了,而且现在主要目的是温习数据结构和算法的知识,所以只能放弃用c的想法,以后如果需要再学习,先用最熟悉的java来实现代码)
下面来看具体的操作和逻辑,附带贴上代码。
我们直接说最麻烦的删除节点吧!!
首先我们要删除一个节点,而这个节点他可能有左子节点或者右子节点或者没有子节点。。就比如图中
(1)我要删除55这个节点,我们可以直接删除他,中序遍历的结果还是很正常
(2)我要删除53这个节点,这是个有左无右的节点,那我们可以直接让被他的左子节点取代
(3)我要删除67或者98这种节点,因为他们都有右子树,我们就要找到右子树的最小值来作为前继节点(比要删除的节点大的节点里最小的)用来取代当前node的值,并且把前继节点从原先位置删除!
具体实现代码如下所示:
public class SearchTree {
private TreeNode root;
public SearchTree() {
}
// 中序遍历(递归)
public void midOrder(TreeNode node) {
if (node == null) {
return;
}
// 对该节点继续进行左右子节点的遍历
// 先输出根节点,因为这是前序遍历,根左右
midOrder(node.lchild);
System.out.println("二叉树节点 : " + node.data);
midOrder(node.rchild);
}
public TreeNode putTreeNode(int key) {
TreeNode node = null;
TreeNode parent = null;
if (root == null) {
node = new TreeNode(0, key);
root = node;
}
// 如果根节点已经存在,就要开始判断了
node = root;
while (node != null) {
parent = node;
if (key > node.data) {
// 获取右节点
node = node.rchild;
} else if (key < node.data) {
// 获取左节点
node = node.lchild;
} else {
// 相等的话,就啥也不做
return node;
}
}
// 如果跳出了循环,代表这个节点不存在,需要创建
node = new TreeNode(0, key);
// 找到此时node的父节点
if (key > parent.data) {
parent.rchild = node;
} else if (key < parent.data) {
parent.lchild = node;
}
node.parent = parent;
return node;
}
// 删除节点
public void deleteNode(int key) {
TreeNode node = searchNode(key);
if (node == null) {
throw new RuntimeException("查找该节点不存在!!");
}
delete(node);
}
public void delete(TreeNode node) {
if (node == null) {
throw new RuntimeException("删除该节点不存在!!");
}
TreeNode parent = node.parent;
if (node.lchild == null && node.rchild == null) {
// 直接删除,不要顾及太多
if (parent.lchild == node) {
parent.lchild = null;
}
if (parent.rchild == node) {
parent.rchild = null;
}
return;
}
// 如果是有左无右的,左节点默认是要删除节点的后继节点
if (node.lchild != null && node.rchild == null) {
if (parent.lchild == node) {
parent.lchild = node.lchild;
}
if (parent.rchild == node) {
parent.rchild = node.lchild;
}
return;
}
// 如果是有右无左或者是有右有左,我们都选择拿到右子树的最小值当前继节点
// 我们首先获取到前继节点
TreeNode next = getNextNode(node);
// 我们要确定一点的是,我们拿到的前继节点一定是没有左子节点的
// 拿到前继节点后,我们要删除这个节点,
// 就是说要把前继节点的右子树设置为前继节点的父节点的左子树
delete(next);
// 把前继节点的值赋值给要删除的node
node.data = next.data;
}
/**
* @param node
* 查找后继节点
* @return
*/
public TreeNode getNextNode(TreeNode node) {
if (node == null) {
return null;
}
// 其实既可以找左子树最大的那个值也可以找右子树最小的值
if (node.rchild != null) {
// 这里选择的是拿右子树最小的值
// 找某节点最小关键字节点(右子树最小值)
return getMinTreeNode(node.rchild);
}
return null;
}
private TreeNode getMinTreeNode(TreeNode node) {
// 一直找左孩子
if (node == null) {
return null;
}
TreeNode parent = null;
while (node != null) {
parent = node;
node = node.lchild;
}
return parent;
}
// 查找节点
public TreeNode searchNode(int key) {
if (root == null) {
return null;
}
TreeNode node = root;
while (node != null) {
if (key > node.data) {
node = node.rchild;
} else if (key < node.data) {
node = node.lchild;
} else {
return node;
}
}
// 跳出了上面循环的话,就代表没有该节点。。。
return null;
}
public class TreeNode {
private int index;
private int data;
private TreeNode lchild;
private TreeNode rchild;
private TreeNode parent;
public TreeNode(int index, int data) {
this.index = index;
this.data = data;
}
}
public static void main(String[] args) {
SearchTree searchTree = new SearchTree();
int[] array = { 50, 30, 15, 45, 60, 55, 70, 58 };
for (int data : array) {
searchTree.putTreeNode(data);
}
searchTree.midOrder(searchTree.root);
System.out.println("============");
searchTree.deleteNode(60);
searchTree.midOrder(searchTree.root);
}
}




