《BI那点儿事》三国人物智力分布状态分析
献给广大的三国爱好者们,希望喜欢三国的朋友一起讨论,加深对传奇三国时代的了解
数据分析基础概念:
数据分为“不可测量”的数据和“可测量”的数据。
不可测量的数据称为“分类数据”(Category Data或Categorical Data。),而可测量的数据称为“数值数据”(Numerical Data)。
组中值:Class Midpoint
次数:Frequency
相对次数:Relative Frequency
相对次数=所属各组的数据个数÷数据总数
次数分布表和直方图
组距分组掩盖了各组内间的数据分布状况,为反映各组数据的一般水平,我们通常用组中值来作为该组数据的一个代表值(class midpoint)。上限与下限之间的中点数值称为组中值,它是各组上下限数值的简单平均,即组中值=(下限+上限)/2。
若遇到开口组,则上开口组组中值=下限+邻组组距/2; 下开口组组中值=上限-邻组组距/2。
使用组中值代表一组数据时有一个必要的假定条件,即各组数据在本组内呈现均匀分布或在组中值两侧呈对称分布。如果实际数据的分布不符合这一假定,用组中值作为一组数据的代表就会有一定的误差。
建立数据分析环境:
SELECT CASE WHEN 智力 > 0 AND 智力 < 10 THEN '0-9' WHEN 智力 >= 10 AND 智力 < 20 THEN '10-19' WHEN 智力 >= 20 AND 智力 < 30 THEN '20-29' WHEN 智力 >= 30 AND 智力 < 40 THEN '30-39' WHEN 智力 >= 40 AND 智力 < 50 THEN '40-49' WHEN 智力 >= 50 AND 智力 < 60 THEN '50-59' WHEN 智力 >= 60 AND 智力 < 70 THEN '60-69' WHEN 智力 >= 70 AND 智力 < 80 THEN '70-79' WHEN 智力 >= 80 AND 智力 < 90 THEN '80-89' WHEN 智力 >= 90 AND 智力 <= 100 THEN '90-100' END 分组 , COUNT(*) 人数 FROM FactSanguo11 GROUP BY CASE WHEN 智力 > 0 AND 智力 < 10 THEN '0-9' WHEN 智力 >= 10 AND 智力 < 20 THEN '10-19' WHEN 智力 >= 20 AND 智力 < 30 THEN '20-29' WHEN 智力 >= 30 AND 智力 < 40 THEN '30-39' WHEN 智力 >= 40 AND 智力 < 50 THEN '40-49' WHEN 智力 >= 50 AND 智力 < 60 THEN '50-59' WHEN 智力 >= 60 AND 智力 < 70 THEN '60-69' WHEN 智力 >= 70 AND 智力 < 80 THEN '70-79' WHEN 智力 >= 80 AND 智力 < 90 THEN '80-89' WHEN 智力 >= 90 AND 智力 <= 100 THEN '90-100' END ORDER BY 分组 SELECT * FROM FactSanguo11 WHERE 智力 >= 90 AND 智力 <= 100 ORDER BY 智力 DESC
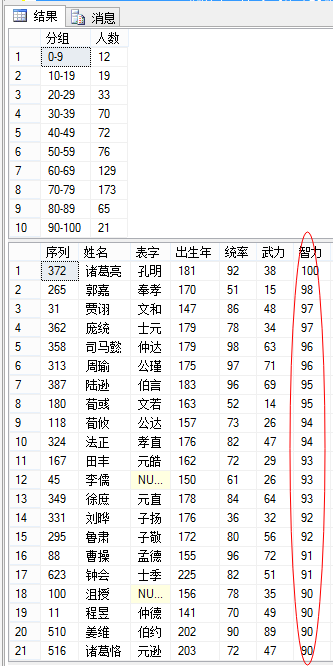
三国人物智力分布表
|
智力分组 |
组中值 |
人数 |
相对次数 |
|
0-9 |
5 |
12 |
0.02 |
|
10-19 |
14.5 |
19 |
0.03 |
|
20-29 |
25 |
33 |
0.05 |
|
30-39 |
34.5 |
70 |
0.10 |
|
40-49 |
44.5 |
72 |
0.11 |
|
50-59 |
54.5 |
76 |
0.11 |
|
60-69 |
64.5 |
129 |
0.19 |
|
70-79 |
74.5 |
173 |
0.26 |
|
80-89 |
84.5 |
65 |
0.10 |
|
90-100 |
95 |
21 |
0.03 |
|
合计 |
|
670 |
1.00 |
直方图: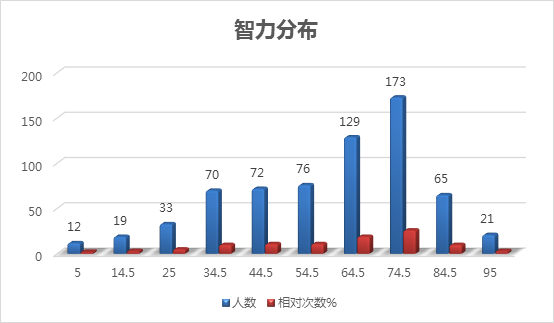
如各位所见,上表中的组距是9。之所以选择9,并没有什么数学上的规定,而是全由本人主观决定的。没错,组距该设多少,完全依照分析者本身的判断。
以主观设定的组距而做成的人数分布表没有说服力,无法在他人面前公开,难道就没有按数学原理制定组距的方法吗?也许有人会产生这样的疑问。事实上,方法是有的。

以步骤2求出的组距为基础,做出如下的人数分布表:
|
智力分组 |
组中值 |
人数 |
相对次数 |
|
0-10 |
5 |
13 |
0.02 |
|
11-20 |
15 |
18 |
0.03 |
|
21-30 |
25 |
39 |
0.06 |
|
31-40 |
35 |
71 |
0.11 |
|
41-50 |
45 |
70 |
0.10 |
|
51-60 |
55 |
78 |
0.12 |
|
61-70 |
65 |
146 |
0.22 |
|
71-80 |
75 |
160 |
0.24 |
|
81-90 |
85 |
58 |
0.09 |
|
91-100 |
95 |
17 |
0.03 |
|
合计 |
|
670 |
1.02 |
直方图:
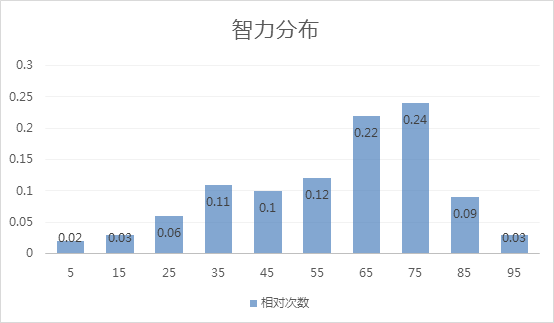





 浙公网安备 33010602011771号
浙公网安备 33010602011771号