FDR错误发现率-P值校正学习[转载]
转自:https://baike.baidu.com/item/FDR/16312044?fr=aladdin https://blog.csdn.net/taojiea1014/article/details/79681249
http://www.360doc.com/content/18/0914/21/19913717_786724085.shtml https://www.sohu.com/a/165109778_785442
https://www.jianshu.com/p/13f46bebebd4
1.定义
FDR(false discovery rate),是统计学中常见的一个名词,翻译为伪发现率,其意义为是 错误拒绝(拒绝真的(原)假设)的个数占所有被拒绝的原假设个数的比例的期望值。

//FDR是个期望值
2.利用Benjamini–Hochberg方法计算FDR的计算及R语言实现
FDR的计算相当简单,包括以下几步:
1.对p值进行从小到大的排序,标记上序号1~n;
2.其中,最大的FDR(不考虑重复则为第n位)等于最大的p值;
3.对于n-1位的FDR,取下面两者的较小值:
-
上一步(第n位)计算得出的FDR值;
-
p值*n/(n-1)
4.不断迭代第三步(n-2,n-3....),直至计算到最小p值对应的FDR。
例子:
temp <-c(0.01,0.11,0.21,0.31,0.41,0.51,0.61,0.71,0.81,0.91) p.adjust(temp,method = "fdr") 结果: [1] 0.1000000 0.5500000 0.7000000 0.7750000 0.8200000 0.8500000 0.8714286 [8] 0.8875000 0.9000000 0.9100000
另外,如果对temp的倒数第二个P值进行更改:
temp2 <-c(0.01,0.11,0.21,0.31,0.41,0.51,0.61,0.71,0.90,0.91) p.adjust(temp2,method = "fdr") [1] 0.1000000 0.5500000 0.7000000 0.7750000 0.8200000 0.8500000 0.8714286 [8] 0.8875000 0.9100000 0.9100000
第一次:min(0.91,0.81*10/9)=0.90
第二次:min(0.91,0.90*10/9)=0.91
分别演示了两个取到不同值的过程。
这样可以保证从统计学上FDP不超过q。
3.确定FDR

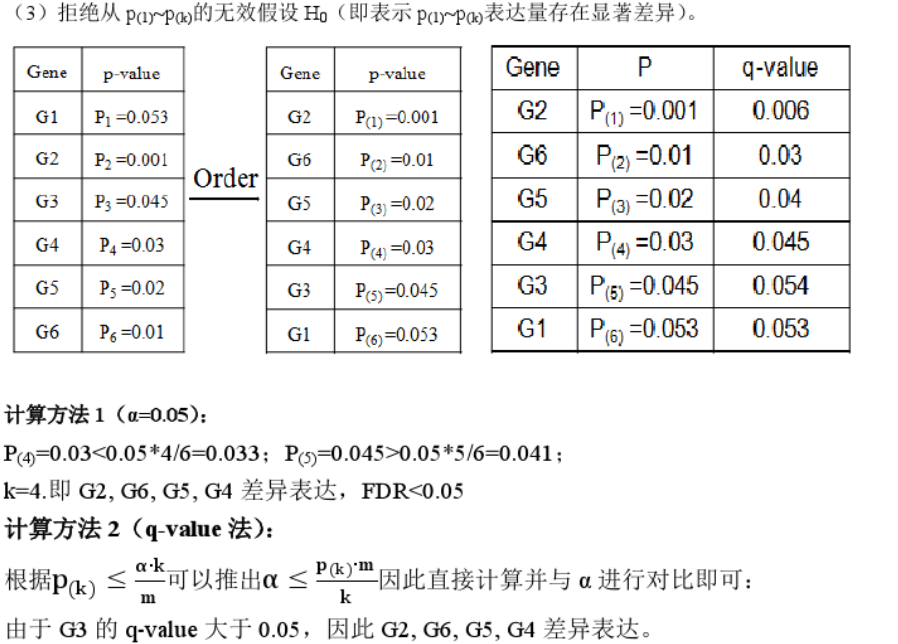
3.只使用P值的话
单次检验:针对单个基因(蛋白),采用统计检验,假设采用的p值为小于0.05,我们通常认为这个基因在两个(组)样本中的表达是有显著差异的,但是仍旧有5%的概率,这个基因并不是差异基因。
注:原假设是两个基因不存在显著性差异。
多次检验:当两个(组)样本中有10000个基因采用同样的检验方式进行统计检验时,这个时候就有一个问题,单次犯错的概率为0.05, 进行10000次检验的话,那么就有0.05*10000=500 个基因的差异被错误估计了。
有一种严格校正法:
Bonferroni 校正法
Bonferroni校正法:如果进行N次检验,那么p值的筛选的阈值设定为p/N。 比如,进行10000次检验的话,如果p值选择为0.05, 那么校正的p值筛选为0.000005。 p值低于此的基因才是显著性差异基因。
该方法虽然简单,但是过于严格,导致最后找的差异基因很少,甚至找不到差异的基因。
4.假设检验

我们在处理宏基因组差异基因的选择时,需要对两个样本的每个基因进行一次假设检验。如果我们有m个基因,那么我们就要做m次假设检验。每一次的假设检验的零假设H0为:两个样本的这个基因没有显著性差异。其中有m0个零假设是正确的,即这个基因在两个样本中确实没有显著性差异;但有m1=m-m0个零假设是错误的,即两个样本的这个基因是有显著性差异。m次检验之后,被拒绝的零假设的个数记为R。为了方便记忆,可用一张表格来表示假设检验的结果,如上。
我们可以得到FDR准则,即要求控制错误拒绝率。令Q=V / (V+S),它表示被错误拒绝的零假设数目占所有被拒绝的零假设数目的比例。Q也是一个不可观测的随机变量。
https://stackoverflow.com/questions/10323817/r-unexpected-results-from-p-adjust-fdr
这个里讲了如何计算及过程,明天来总结。
5.R中的cummin函数
> cummin(c(3:1, 2:0, 4:2)) [1] 3 2 1 1 1 0 0 0 0 > c(3:1, 2:0, 4:2) [1] 3 2 1 2 1 0 4 3 2 #求从左到右累积的最小值。 #到第二个2出现时已经有了最小值是1,所以对应都是1. #到第一个0出现时,是最小值,那么对应之后再出现的4 3 2 累计最小值都是0.


