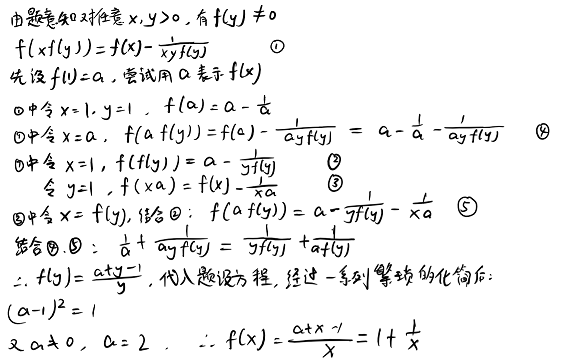奥赛经典（代数篇）划水记

转载请注明链接 http://www.cnblogs.com/Blog-of-Eden/p/8971594.html，谢谢~

 

4月29日，1~9

　　ZJOI结束了，感觉该做点数学题提神醒脑。于是挑了几道奥赛经典上的几题划划水~~

6月23日，10~12

　　Update：期末考试结束了，来填填坑~

7月20日，13~17

　　Update：暑假玩疯了，学习一下不动点冷静一下

7月21日，18~21

　　Update：奥经上有一些小错误？进行一些修正。凸函数真奇妙

7月22日，22~24

　　Update：函数方程

 

1、一个数集的和是指它的所有元素的和，令S是一些不超过15的正整数组成的集合，

S的任意两个不相交的子集合的和不相等，并且在所有具有上述性质的集合中，S的和最大。

求集合S的和。

（第二章·习题B·1）

 

先证明集合大小不超过5，然后构造即可。答案：61

 

 

2、n是一个正整数，A是集合{1,2,...,n}的子集的一个集合，使得A内无元素包含A的其他元素。

求A的全部元素的个数的最大值。

（第二章·习题B·3）

 

我的大致想法是，对于A内子集，如果最小的大小为k，且k<[n/2]，

我们把所有包含这些子集的大小为k+1的子集去替换这些大小为k的子集，这样A依然合法，并且容易证明元素个数不会减少。

　　（大致证明：S1为大小为k的子集的集合，设S2为大小为k+1的子集的包含这些子集的集合。

　　S1内任意元素对应S2中(n-k)个元素，S2中任意元素最多对应S1中(k+1)个元素。

　　因为n-k>=k+1，又因为对应关系是互相的，所以S2元素个数>=S1元素个数）

对于A内子集，如果最大的大小为k，且k>[n/2]，

我们把所有被这些子集包含的大小为k-1的子集去替换这些大小为k的子集，这样A依然合法，同理容易证明元素个数不会减少。

于是，当A内子集大小都为[n/2]时，A的全部元素个数最大。

此时元素个数为C(n,[n/2])。

 

题解做法比较有趣，对于1到n的全排列，种数为n!个。设A中有fk个k元子集作为元素。|A|=f1+f2+...+fn

当fk>0，对于fk个k元子集中任意一个子集{a1,a2,...,ak}，取出前k个元素恰好构成子集{a1,a2,...,ak}的全排列，共有k!(n-k)!个。

由于A中两两元素不包含。因此对于A中所有元素用上述方法取出的全排列必然两两不同。

所以，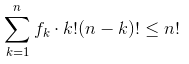

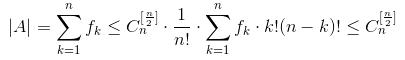
当A取{1,2,...,n}中全部[n/2]元子集组成的集合时，恰达到|A|=C(n,[n/2])

 

 

3、n是不小于3的正整数，f(n)表示不是n的因数的最小正整数（例如f(12)=5）。

如果f(n)≥3，又可作f(f(n))，类似的，如果f(f(n))≥3，又可作f[f(f(n))]等等。

如果f(f(···f(n)···))=2 （前面有k次f），就把k叫做n的长度。

如果用Ln表示n的长度，试对任意正整数n(n≥3)，求Ln，并证明你的结论。

（第三章·习题B·2）

 

显然，当n是奇数时Ln=1。

当n为偶数时，设n=2^k * (2m+1) （k是正整数，m是非负整数）

若 1,2,...,2^(k+1)-1 都是n的约数，那么显然f(n)=2^(k+1)，Ln=3。

其他情况下，f(n)一定是个奇数，故Ln=2。

 

 

4、函数f(x,y)对所有的非负整数x,y满足：

　　1.f(0,y)=y+1

　　2.f(x+1,0)=f(x,1)

　　3.f(x+1,y+1)=f[x,f(x+1,y)]

　　试确定f(4,1981)

（第三章·习题B·4）

 

f(0,n)=n+1

f(1,0)=2，f(1,n) = f(0,f(1,n-1)) = f(1,n-1) +1，故 f(1,n)=n+2

f(2,0)=3，f(2,n) = f(1,f(2,n-1)) = f(2,n-1) +2，故 f(2,n)=2n+3

f(3,0)=5，f(3,n) = f(2,f(3,n-1)) = 2*f(3,n-1)+3，故 f(3,n) = 2^n *8-3

f(4,0)=13，f(4,n) = f(3,f(4,n-1)) = 2^f(4,n-1) *8 - 3。设g(n) = f(4,n)+3，g(n) = 2^g(n-1)

则又g(0) = 2^2^2，g(1981) = 2^2^2^2...^2（1983次^2，一共1984个2）

f(4,1984) = 2^2^2^2...^2（1983次^2，一共1984个2）- 3

 

 

5、设a与d是非负数，b与c是正数，并且b+c≥c+d，试求下式的最小值：

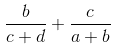
（第四章·习题A·5）

 

题解做法真是妙啊

不妨设a+b≥c+d

原式=(b+c)/(c+d) - c*(1/(c+d)-1/(a+b))

　　≥(a+b+c+d)/(2c+2d) - (c+d)*(1/(c+d)-1/(a+b))

　　=(a+b)/(2(c+d)) - 1/2 +(c+d)/(a+b)

　　≥2*sqrt(1/2) -1/2

　　=sqrt(2) - 1/2

等号成立当且仅当 d=0，b+c=a+d，sqrt(2) (c+d) = a+b

当a=sqrt(2)+1, b=sqrt(2)-1, c=2, d=0，原式最小值为 sqrt(2) - 1/2

 

 

6、设x,y是正数，S是x,y+1/x,1/y中最小的数，求S的最大可能值。x,y取何值时能达到最大值？

（第四章·习题B·2）

 

我的想法是，原题显然可以换1/y为y'。S=min(x,1/x+1/y',y')。求S的最大值。

　　x,y可以交换，所以不妨设x<=y。显然一定存在x<=z<=y，使得1/z+1/z=1/x+1/y'（f(x)=1/x（x>0）函数的连续性）

　　而此时min(z,z,1/z+1/z) >= min(x,y',1/x+1/y')

　　所以可以证明，当S取得最大值时，x等于y'。S=min(x,2/x)。显然x=sqrt(2),y=sqrt(2)/2时，S达到最大值sqrt(2)。

题解有一个更自然的做法。S<=x，S<=y+1/x，S<=1/y，且三个不等式中至少有一个等号成立。

　　S<=y+1/x<=1/S+1/S=2/S。S<=sqrt(2)。

　　而当x=sqrt(2),y=sqrt(2)/2时，S恰好达到最大值sqrt(2)。

 

 

7、n个正数x1,x2,...,xn之和等于1，设S是下列各数中最大的数：

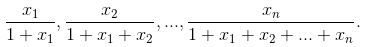
求S的最小可能值，x1,x2,...,xn取何值时能达到最小值？

（第四章·习题B·3）

 

我们设Si = xi/(1+x1+x2+...+xi)。那么S=max(S1,S2,...,Sn)。要使S最小。

显然(1-S1)*(1-S2)*...*(1-Sn) = 1/2

显然一定存在一个 1-Si <= 2^(-1/n)。即一定存在一个Si>=1-2^(-1/n)。

所以我们得出结论：S>=1-2^(-1/n)

当S=1-2^(-1/n)时，显然S1=S2=...=Sn=1-2^(-1/n)。

我们尝试构造解，当xi=2^(i/n) - 2^((i-1)/n)时，S=1-2^(-1/n)

 

 

8、求函数的最小值

（第五章·习题B·3）

 

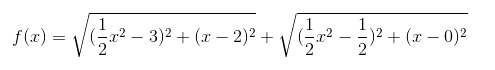
在抛物线y^2=2x上取一个点P，使得它到点A(3,2)，点B(1/2,0)的距离和最小。

容易发现，A在抛物线内部，点B(1/2,0)恰好是抛物线焦点，

根据抛物线定义，P到B的距离恰好等于P到准线x=-1/2距离。

PA+PB=AP+P到准线距离>=A到准线距离=7/2。当过A做准线垂线交抛物线于点P时，等号成立。故最小值为7/2。

 

 

9、求函数的最小值

（第五章·习题B·5）

 

方法一（粗暴的方法）：，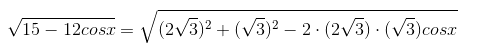

通过余弦定理得知该式的值为两边分别为2sqrt(3)，sqrt(3)，夹角为x，第三条边的长度。

第二、第三个式子同理。第四个式子：

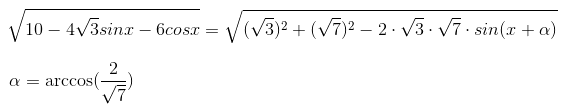
于是题目可以转换成，A(0, 2sqrt(3)), B(1,0), C(2,0), D(2,sqrt(3)，OP=sqrt(3)，求PA+PB+PC+PD最小。

我们发现以O为圆心，sqrt(3)为半径的圆与AC相切，切点(3/2,sqrt(3)/2)在BD上。

故P取(3/2,sqrt(3)/2)时，PA+PB+PC+PD的值最小，为6

 

方法二（题解的做法就正常多了）：

 

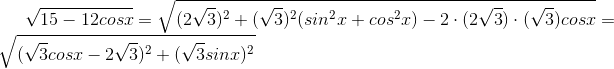
可看做P与原点距离为sqrt(3)，即P坐标为(sqrt(3)cosx,sqrt(3)sinx)，该式的值就是P到(2sqrt(3),0)的距离。

以此类推，最后回到P到A、B、C、D四点距离最小值问题。和方法一一样。

答案为6。

 

 

 10、求函数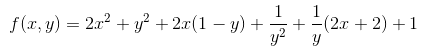的最小值

（第五章·习题B·8） 

 

方法一：

凑一凑平方，然后不等式暴算

 

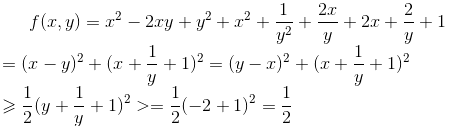
当等号成立。f(x,y)最小值为1/2。

方法二（题解做法）：

题解似乎很喜欢用数形结合？

 

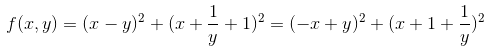
即两函数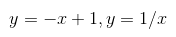上的点的最近距离的平方。

故最近距离显然是sqrt(2)/2，最小值为1/2。

 

 

11、设x,y∈R+，求函数

的最小值.

（第五章·例12） 

 

数形结合大法好啊。

如图，EA,EB,EC,ED之间相邻两条射线夹角为30°。

EA=ED=sqrt(3)

EB=x,EC=y。

可知原式的值为AB+BC+CD，最小值为AD=sqrt(6)

 

 

 12、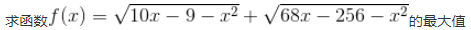

 （第五章·例15） 

 

容易看出可以根号下可以因式分解

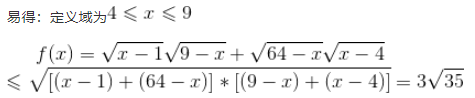
所以f(x)最大值为3sqrt(35).

 

 

13、设{f(n)}是取正整数值的严格递增序列。已知 f(2) = 2，当m,n互质时，f(m·n) = f(m)·f(n)

　　求证：f(n) = n

（第六章·例2）

 

 

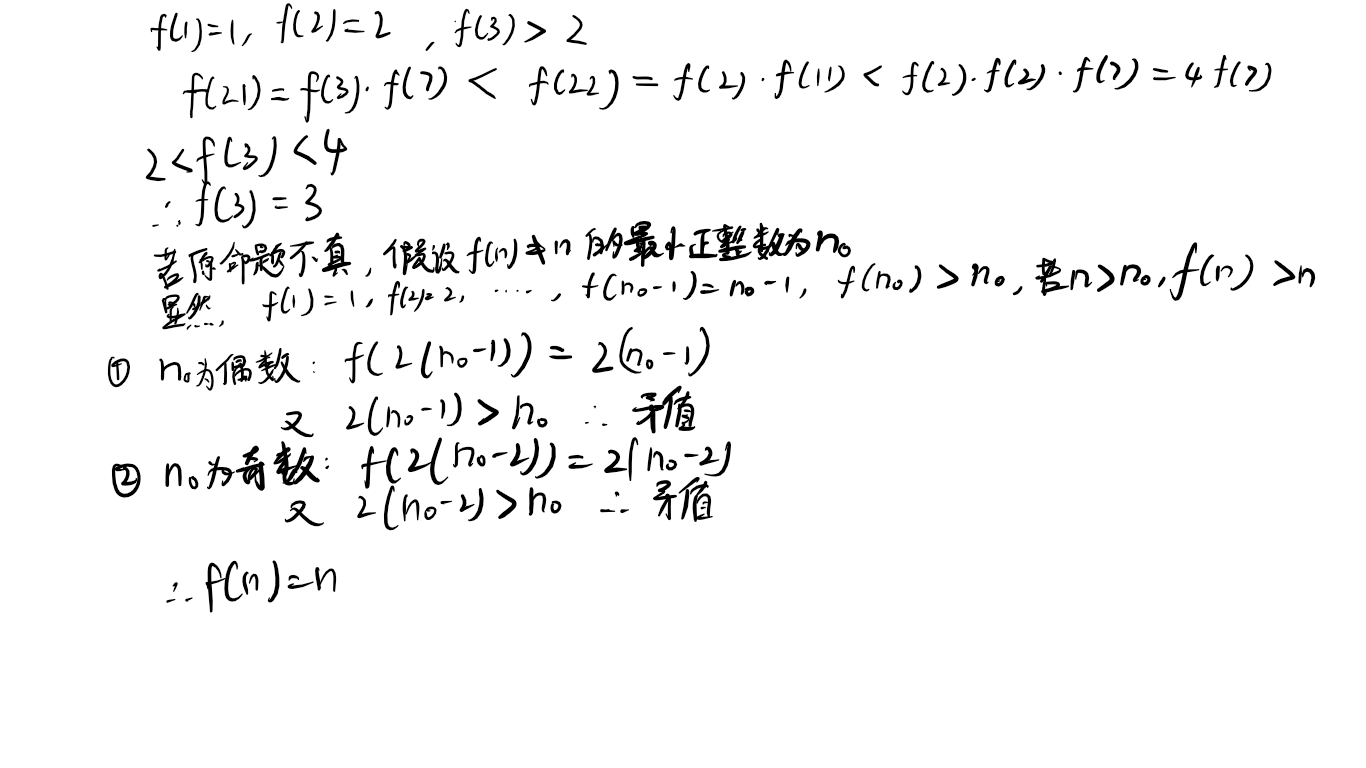
14、利用f(x)的不动点解方程

 

 

 

15、求出所有的函数f，它的定义域为一切正实数，并且函数值为正实数，满足下述条件：

　　(1). f[xf(y)] = yf(x) , 对任意x,y∈R+

　　(2). 当x->∞时，f(x)->0

（第六章·例6）

 

 

 

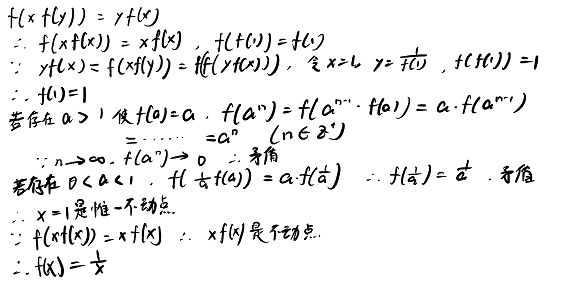
16、证明不存在任意实数x均满足f[f(x)] = x^2 - 1996的函数f(x)

（第六章·习题B·3）

 

 

 

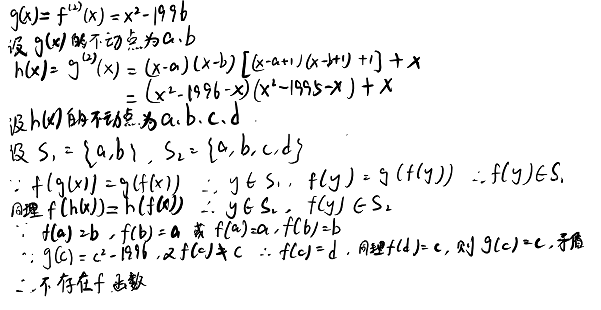
17、设p1(x)=x^2-2，pj(x) = p1[p(j-1)(x)]。试证：对于任意自然数n，pn(x)的所有不动点全是相异的实数。

（第六章·习题B·1）

 

三角换元真是妙啊！

 

 

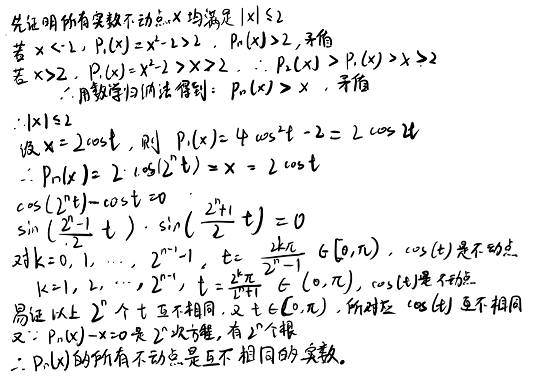
18、试证：若函数f(x)在区间I上是平方下凸，也是几何下凸的，则一定是算术下凸的。

（第七章·例2）

 

　

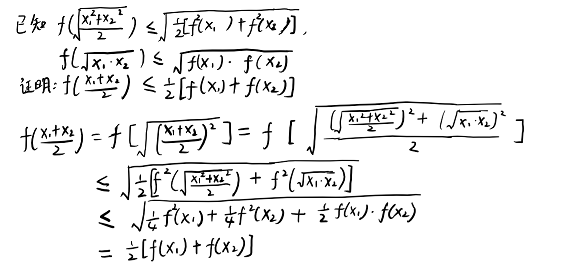
　　试证：函数f(x) = 1/x^k + a（x>0，a,k∈R+）是0类下凸函数

（第七章·例3） 

 

 

 

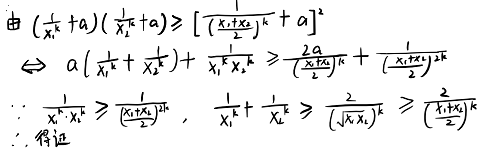
19、已知m≥0，f(x)=x^2+sqrt(m)*x+m+1。求证：对一切x1,x2,…,xn∈R+，均有

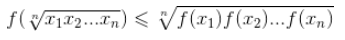
其中等号成立当且仅当x1=x2=...=xn成立。

（第七章·例8）

 

奥经给了一种有趣的归纳法：

 

 

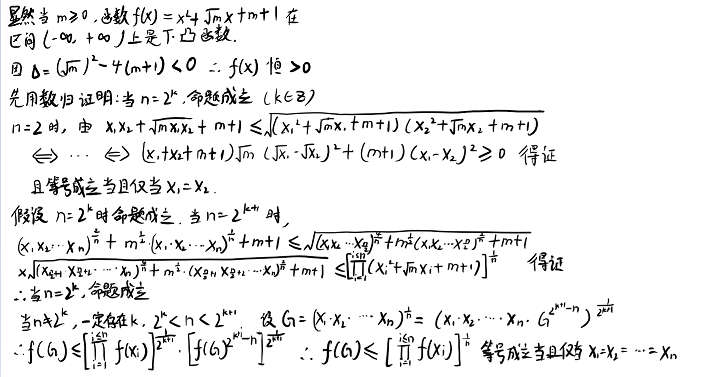
20、设xi∈R(i=1,2,...,n)，x1+x2+...+xn = 1，k,m∈N+。求证：

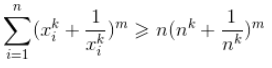
（第七章·习题A·2）

 

不是很理解题解的最后一句话（谁懂的话教教我吧），所以这里搬上自己的做法

与 习题B·2 做法类似

 

 

21、试证：幂函数f(x)=x^a（x>0，0<a<1）是上凸函数。

（第七章·例1）

 

题解给出了一种神奇的做法

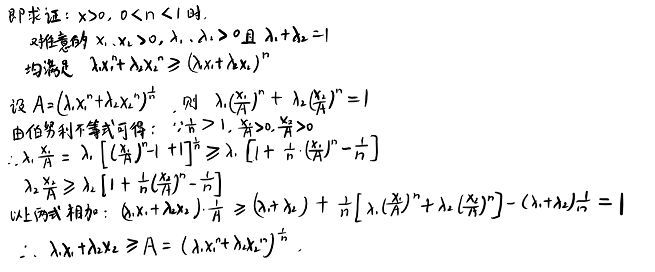
上述伯努利不等式可由求导轻松证明

 

 

22、试求所有函数f:Z->Z，使得对一切n∈Z，有f[f(n)]+f(n)=2n+3，且f(0)=1

（第八章·例3）

 

感觉更像数学归纳题？

 

 

23、设函数f(x)对所有x>0有定义，且满足下面条件：

(i) 函数f(x)在(0,+∞)上严格递增；

(ii) 对所有x>0，均有f(x)>-1/x

(iii) 对所有x>0，均有f(x)·f[f(x)+1/x]=1

（1）求函数值f(1)

（2）给出一个满足(1)中三个条件的函数.

（第八章·例6）

 

虽然比较容易，但答案带根号真是意想不到

 

 

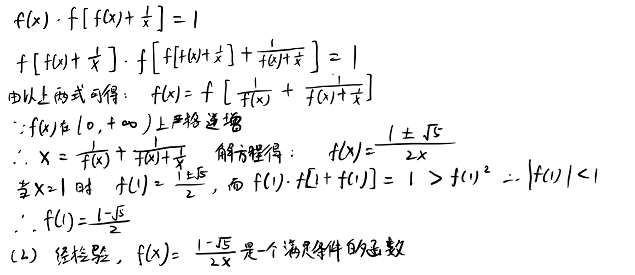
24、求所有的函数f:R+->R+，满足对任意的x,y∈R+，f(x)·f(y)=f(y)·f[xf(y)]+1/(xy)。

（第八章·例9）

 

捷克和斯洛伐克的题好难啊。。

至关重要的一步：令x=f(y)