TopCoder SRM 566 Div 1 - Problem 1000 FencingPenguins
传送门:https://284914869.github.io/AEoj/566.html
题目简述:
平面上有中心在原点,一个点在(r,0)处的正n边形的n个顶点。
平面上还有m个企鹅,每个企鹅有一个位置和一个颜色,
现在要连一些边,使得每个点的度数都是0或2,
这样会构成若干个顶点不相交的圈,求满足以下条件的连边方案数:
1、每个圈里有至少一个企鹅;
2、任意两个圈不相交;
3、每种颜色的企鹅在同一个有限区域中;
4、每个企鹅在一个有限区域内;
n<=222,m<=50,r<=10^5,
企鹅的颜色保证是大写字母或者小写字母,
坐标范围<=10^5,企鹅离任一条n个点连的边的距离>10^-6
思路:
很显然这题要用dp。考虑怎么用dp做。
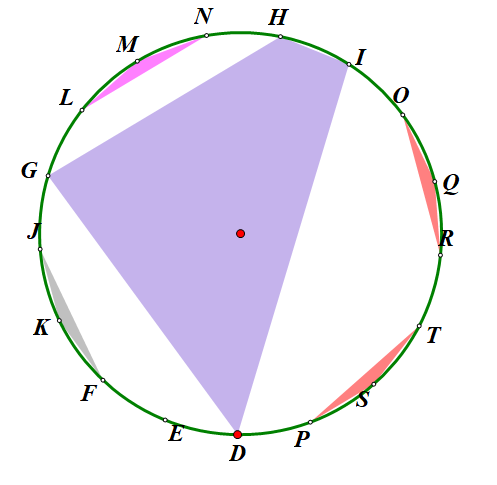
如图所示
我们先定义“特殊”多边形为有>=3条边的多边形或一个点。如图有6个多边形(包括点E)。
这样所有的点就都在多边形上了。
我们选任意一个点作为起点。例如D。
D所在的多边形为DGHI。这样弧DG,GH,HI,ID上的点形成的多边形就是互不干扰的了。
所以初步构思,可以从若干个小弧的状态推到一个大弧的状态。(我可能说不清楚具体过程,感性理解)
还有一个问题就是同颜色的企鹅在同一个多边形内。
这个限制可以转换为,所有的边两侧不存在同颜色的企鹅,且所有企鹅都不在多边形外部。
那么写起来就更方便了。
代码:
1 #include <cmath> 2 #include <cstdio> 3 #include <string> 4 #include <vector> 5 #include <cstring> 6 #include <iostream> 7 #include <algorithm> 8 using namespace std; 9 #define _CLASSNAME_ FencingPenguins 10 #define _METHODNAME_ countWays 11 #define _RC_ int 12 #define _METHODPARMS_ int _n, int _r, vector<int> _x, vector<int> _y, string _c 13 #define ref(i,x,y)for(int i=x;i<=y;++i) 14 #define def(i,x,y)for(int i=x;i>=y;--i) 15 #define reset(a)memset(a,0,sizeof a) 16 const double pi=acos(-1); 17 const int mod=100007; 18 struct point{ 19 double x,y; 20 point(){x=0;y=0;} 21 point(double X,double Y){x=X,y=Y;} 22 }; 23 point operator -(point a,point b){ return point(a.x-b.x,a.y-b.y); } 24 double operator ^(point a,point b){ return a.y*b.x-a.x*b.y; } 25 int n,m,r,ans; 26 int p_c[51],fg[52],sum[445][445]; 27 point O[301],p[51]; 28 bool ok[445][445]; 29 void inc(int&a,int b){a+=b;if(a>=mod)a-=mod;} 30 int mul(int a,int b){return 1LL*a*b%mod;} 31 int chd(char c){if(c>='a'&&c<='z')return c-'a';else return c-'A'+26;} 32 void work1(){ 33 reset(ok); reset(sum); ans=0; 34 ref(i,0,n-1) O[i]=point(r*cos(2*pi*i/n),r*sin(2*pi*i/n)); 35 ref(i,0,n-1)ok[i][i]=1; 36 ref(i,0,n-1)ref(j,i+1,n-1){ 37 ref(k,0,51)fg[k]=0; 38 ref(k,1,m){ 39 int C=p_c[k]; double s=(O[j]-O[i])^(p[k]-O[i]); 40 if(!fg[C])fg[C]=(s>0)+1;else if(fg[C]!=-1) if(fg[C]!=(s>0)+1)fg[C]=-1; 41 sum[i][j]+=(s>0); 42 } 43 bool flag=1; ref(k,0,51)flag=flag&&(fg[k]>=0); 44 ok[i][j]=ok[j][i]=flag; sum[j][i]=m-sum[i][j]; 45 } 46 ref(i,0,n-1)ref(j,0,n-1) sum[i+n][j]=sum[i][j+n]=sum[i+n][j+n]=sum[i][j]; 47 ref(i,0,n-1)ref(j,0,n-1) ok[i+n][j]=ok[i][j+n]=ok[i+n][j+n]=ok[i][j]; 48 } 49 int dp1[445][445][2],dp2[445][445]; bool tri[223][445][445]; 50 void work2() 51 { 52 reset(dp1); reset(dp2); reset(tri); 53 ref(i,0,n-1)if(sum[i][i+1])return; 54 ref(i,0,n-1)ref(j,i,i+n-1)ref(k,i+1,j-1)tri[i][k][j]=(sum[i][j]-sum[i][k]-sum[k][j]>0); 55 ref(i,0,n*2-1)dp1[i][i][1]=1,dp2[i][i]=1; 56 ref(len,1,n-1){ 57 ref(i,0,n-1){ 58 int j=i+len; 59 ref(k,i,j-1) if(!tri[i][k+1][j]&&!tri[i][j][j+1]) 60 if(ok[k+1][j])inc(dp2[i][j],mul(dp2[i][k],dp1[k+1][j][1])); 61 inc(dp1[i][j][0],dp2[i][j-1]); 62 ref(k,i+1,j-1)ref(d,0,1) 63 inc(dp1[i][j][d|tri[i][k][j]],mul(dp1[i][k][d],dp2[k][j-1])); 64 if(j<n)dp1[i+n][j+n][0]=dp1[i][j][0],dp1[i+n][j+n][1]=dp1[i][j][1]; 65 if(j<n)dp2[i+n][j+n]=dp2[i][j]; 66 } 67 } 68 if(!tri[n-1][n][n+1])ans=dp2[0][n-1]; 69 ref(i,2,n-1)if(ok[0][i])inc(ans,mul(dp1[0][i][1],dp2[i][n-1])); 70 } 71 class _CLASSNAME_{ 72 public: 73 _RC_ _METHODNAME_(_METHODPARMS_) 74 { 75 n=_n; m=_x.size(); r=_r; 76 ref(i,1,m)p[i].x=_x[i-1],p[i].y=_y[i-1]; 77 ref(i,1,m)p_c[i]=chd(_c[i-1]); 78 work1();work2(); 79 return _RC_(ans); 80 } 81 82 // BEGIN CUT HERE 83 public: 84 void run_test(int Case) { if ((Case == -1) || (Case == 0)) test_case_0(); if ((Case == -1) || (Case == 1)) test_case_1(); if ((Case == -1) || (Case == 2)) test_case_2(); if ((Case == -1) || (Case == 3)) test_case_3(); if ((Case == -1) || (Case == 4)) test_case_4(); if ((Case == -1) || (Case == 5)) test_case_5(); if ((Case == -1) || (Case == 6)) test_case_6(); if ((Case == -1) || (Case == 7)) test_case_7(); } 85 private: 86 //template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '\"' << *iter << "\","; os << " }"; return os.str(); } 87 void verify_case(int Case, const int &Expected, const int &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << "\tExpected: \"" << Expected << '\"' << endl; cerr << "\tReceived: \"" << Received << '\"' << endl; } } 88 void test_case_0() { int Arg0 = 4; int Arg1 = 10; int Arr2[] = {2}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {1}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "R"; int Arg5 = 3; verify_case(0, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 89 void test_case_1() { int Arg0 = 4; int Arg1 = 10; int Arr2[] = {2,-2}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {1,-1}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "RR"; int Arg5 = 1; verify_case(1, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 90 void test_case_2() { int Arg0 = 8; int Arg1 = 10; int Arr2[] = {8,-8,-8,8}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {1,-1,1,-1}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "BBBB"; int Arg5 = 25; verify_case(2, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 91 void test_case_3() { int Arg0 = 8; int Arg1 = 10; int Arr2[] = {8,-8,-8,8}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {1,-1,1,-1}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "RGBY"; int Arg5 = 50; verify_case(3, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 92 void test_case_4() { int Arg0 = 6; int Arg1 = 5; int Arr2[] = {0,0}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {-4,4}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "rB"; int Arg5 = 6; verify_case(4, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 93 void test_case_5() { int Arg0 = 3; int Arg1 = 5; int Arr2[] = {4}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {3}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "y"; int Arg5 = 0; verify_case(5, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 94 void test_case_6() { int Arg0 = 200; int Arg1 = 100000; int Arr2[] = {1020,30203,2302,203,-12321,-21332,8823,-2133,2323}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {-123,2131,4434,1223,43434,2323,4343,-213,-2325}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "YBYBWWBRr"; int Arg5 = 27547; verify_case(6, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 95 void test_case_7() { int Arg0 = 222; int Arg1 = 1713; int Arr2[] = {1091, 243, 505, 510, 869, 700, 790, 70, 260, 177, 273, 9, 43, -83, -163, -79, -352, -231, -663, -8, -768, -128, -768, -372, -577, -895, -994, -564, -509, -199, -833, -391, -445, -276, -115, -133, -166, -37, 65, 170, 251, 389, 23, 194, 130, 629, 477, 401, 1080, 36}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[0]))); int Arr3[] = {4, 147, 265, 52, 302, 548, 183, 302, 439, 176, 167, 287, 677, 826, 156, 550, 758, 129, 254, 308, 595, 445, 310, 230, 99, -3, -85, -113, -321, -99, -134, -98, -747, -615, -216, -760, -891, -248, -783, -396, -586, -866, -479, -50, -731, -50, -195, -153, -23, -9}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[0]))); string Arg4 = "xidylnzmnsolwfyhgjaegnwgazjbdmfwaldsmqxpowtianiesx"; int Arg5 = 64346; verify_case(7, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); } 96 // END CUT HERE 97 98 }; 99 // BEGIN CUT HERE 100 int main() 101 { 102 _CLASSNAME_ user; 103 user.run_test(-1); 104 } 105 // END CUT HERE

