遍历二叉树的神级方法

给定一棵二叉树的头节点head,完成二叉的先序丶中序丶和后序遍历，如果二叉树的节点为N，要求时间复杂度为O(N),空间复杂度为O（1);

实际使用递归函数来完成遍历都是使用了栈函数，空间复杂度为O(h),h为二叉树的高度。那么我们应该怎么来解决空间复杂度问题呢？

答案就是使用Morris遍历。Morris实质上就是避免使用栈结构，而是下层到上层，下层的空闲指针指向上层的某个节点，从而完成了下层到上层的移动，首先以中序遍历举例

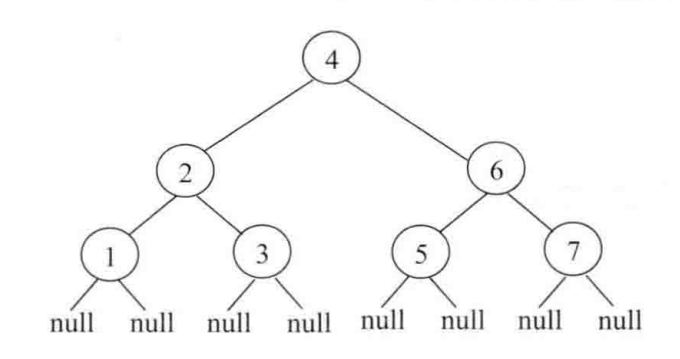
第1步：假设当前子节点的头节点为h,让h的左子树的最右节点的right指针指向h，然后h的左子树继续步骤1的处理过程，直到遇到一某一个节点没有左子树记为Node,进入步骤2

第2步：从node开始通过每个节点的right指针进行移动，并依次打印，假设移动到节点为cur,对每一个cur节点都判断cur的左子树中最右节点是否指向cur

2(1)如果是，让cur结点的左子树的最右结点的right指向空，然后打印，然后让cur的right指针移动到下一个节点（得到右节点）

2（2）如果不是，以cur为头的子树重回步骤1

 

 

using System;
using System.Collections.Generic;

namespace NetFramework
{
    public class BiTree
    {
        public int value;
        public BiTree left;
        public BiTree right;

        public BiTree(int data)
        {
            this.value = data;
        }

        /// <summary>
        /// 中序遍历二叉树，空间复杂度O(1)
        /// </summary>
        /// <param name="head">头节点</param>
        public void MorrishIn(BiTree head)
        {
            //如果头节点为空退出
            if (head == null) return;
            //记录头节点
            BiTree cur1 = head;
            //用来比较判断
            BiTree cur2 = null;
            //如果记录的节点不为空
            while (cur1 != null)
            {
                //找到左孩子，记录起来
                cur2 = cur1.left;
                //如果左孩子有数据
                if (cur2 != null)
                {
                    //判断左孩子的右孩子不为空或指向的不是自己
                    while (cur2.right != null && cur2.right != cur1)
                    {
                        //这里就找到了头结点的左孩子的最右孩子
                        cur2 = cur2.right;
                    }
                    //如果右孩子的数据为空，证明已经是最右了
                    if (cur2.right == null)
                    {
                        //将这个最右的孩子的指针指回头节点
                        cur2.right = cur1;
                        //然后头节点向左孩子移动，这样是为了先找出最左的叶子节点
                        cur1 = cur1.left;
                        //退出继续进入步骤1
                        continue;
                    }
                    else
                    {
                        //将叶子节点的右节点置空
                        cur2.right = null;
                    }
                }
                //如果不符合以上条件证明已经找到要输出的节点，先输出
                Console.Write(cur1.value + " ");
                //然后移动右节点
                cur1 = cur1.right;
            }
        }

    }
}

打印输出了1234567，完成了中序遍历