数据结构（一）-- 平衡树

      文章是对邓俊辉老师数据结构教程的总结，部分图片资料来自邓俊辉老师的教学PPT

     建议阅读前先阅读参考文章的第二，三文章，总结得非常好！

     文章部分代码和图片来自参考文章的第二，三文章！！

阅读前提几个问题吧，帮助思考

为什么需要平衡二叉树
AVL 需要两次旋转的操作为什么不直接分解为左旋和右旋，还要LR RL 呢
AVL 有什么局限性

二叉查找树（Binary Search Tree -- BST）

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

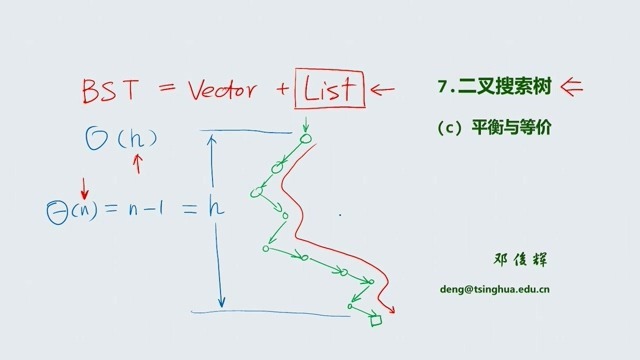
从思路上讲我们希望二叉查找树可以结合向量和链表的结构，但是在某些情况下，时间复杂度还是没能达到要求。

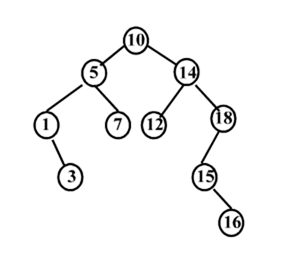
像上面的情况讲，最坏的情况取决于树的高度，当生成像图中的结构时，二叉查找树就成了单链表，查找效率降至O(n)，查找时自然是从第一个查找到最后一个，这样的时间复杂度是无法让人接受的。

理想平衡

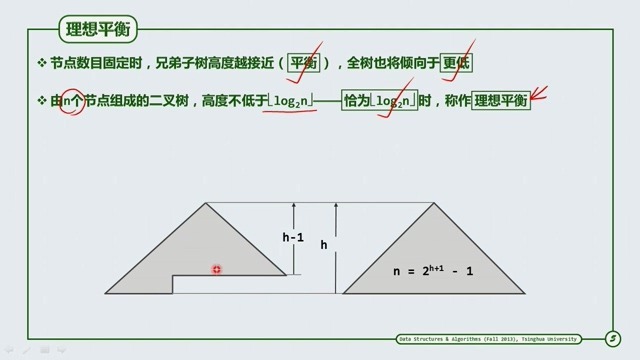
既然二叉搜索树性能取决于其高度，那我们自然想到尽可能降低其高度，使兄弟子树的高度彼此接近。

由于包含n个节点的二叉树，高度不可能小于[log2n]，若恰好高为[log2n]，则称为理想平衡树，如完全二叉树(CBT)、满二叉树均属此类。

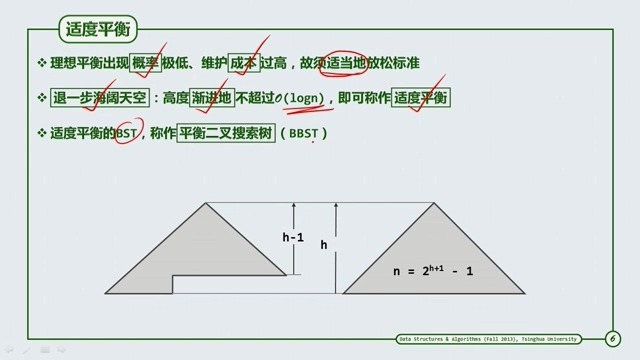
然而，叶节点只能出现于最底两层的限制过于苛刻，此类二叉树所占比例极低，从算法可行性角度来看，应当依照某种相对宽松的标准，重新定义。即是说我们可以约定一定的条件使得某棵树可以接近或是等同于理想平衡树，我们就可以达到目的了，就是下图中的平衡二叉搜索树（Balance BST---BBST）。

至此我们知道了有这么几种树：

二叉搜索树 BST
完全二叉树 CBT
平衡二叉搜索树 BBST

下图解释了理想平衡（理想目标）和适度平衡（追求的目标）

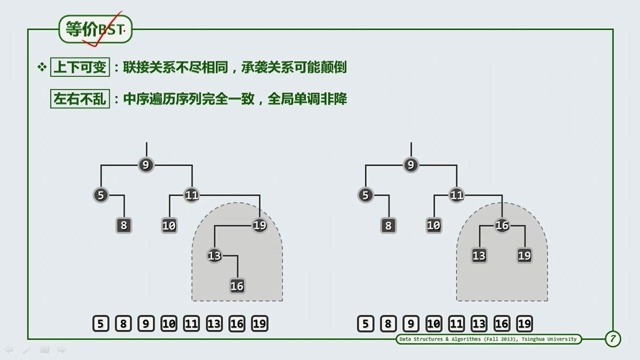
等价BST

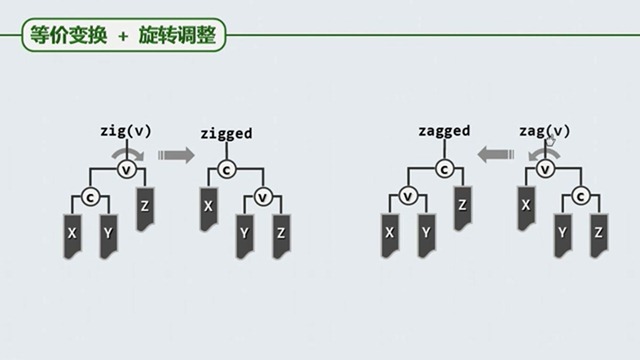
上面这张图可以看到两个平衡树，中序遍历是相同的（树下面的数字），但是扑拓结构是不同的，两者是等价的，他们之间的特点是： 上下可变，左右不乱。（这个非常重要，后面为使树适度平衡实际上就是在依据这两个特点来进行的！！）

两者之间的变换可以通过以下的方式：

可以看到 zig 是顺时针旋转，而 zag 是逆时针旋转，目的是使二叉树平衡。最多操作的次数不要超过 Log_n 次交换（Log_n是适度平衡的树的高度，即是说时间复杂度达到了适度平衡树的高度是最坏的情况----从开始变换到尾）。

我们后面讲的AVL ，remove 方法最坏的情况时间复杂度是 Log_{n ，}所以后面的红黑树等会继续对他改良。

关于的BST 的API方法可以看这一篇文章： http://www.cnblogs.com/penghuwan/p/8057482.html#_label10

AVL (Adelson-Velskii and Landis)

下面部分代码和图片来自参考资料

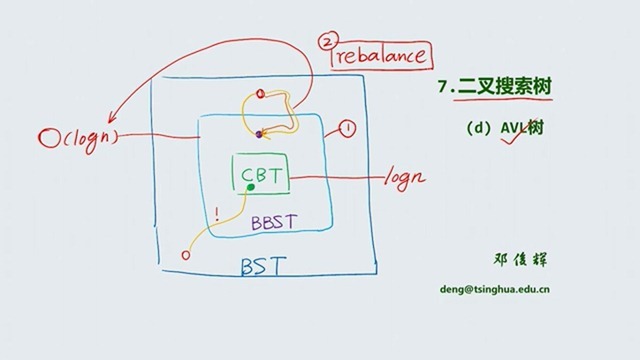
讲 AVL 树之前我们先来看看 CBT BBST BST 之间的关系，我们构建一棵适度平衡的树最重要要解决的两个问题就是：

如何界定BBST
rebalance 的逻辑实现

后面我们会接触到各种适度平衡的树就是围绕这两个方面展开的，回到图中，其中 AVL 就是紫色点（有点小，认真看），存在于BBST中，当失衡的时候跑到了BBST之外，通过rebalance 操作重新回到了 BBST 之中。

下面开始介绍AVL 。AVL 是名字的缩写，是发明这个数据结构的人。学习AVL 这个数据结构之前，我们先对二叉堆高度进行定义

接下来是AVL的定义：（来自维基百科）

In a binary tree the balance factor of a node N is defined to be the height difference

BalanceFactor(N) := Height(RightSubtree(N)) – Height(LeftSubtree(N)) ^[6]

of its two child subtrees. A binary tree is defined to be an AVL tree if the invariant

BalanceFactor(N) ∈ {–1,0,+1}^[7]

holds for every node N in the tree.

平衡因子 = 左子树节点高度 - 右子树节点高度

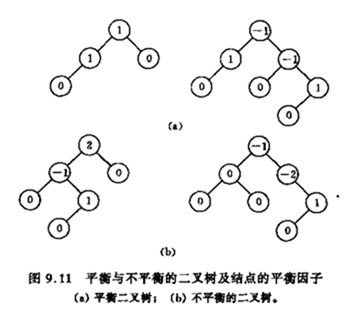
平衡二叉树（AVL）：所有结点的平衡因子的绝对值都不超过1。即对平衡二叉树每个结点来说，其左子树的高度 - 右子树高度得到的差值只能为 1， 0 ， -1 这三个值。取得小于 -1或者大于1的值，都被视为打破了二叉树的平衡。

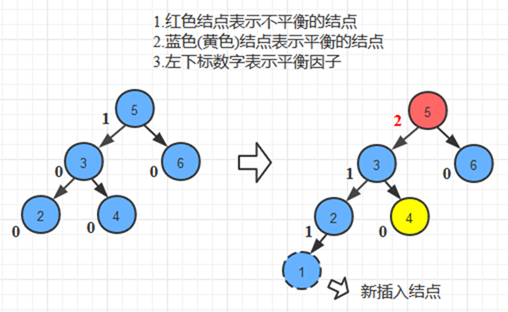
例如下图

为了使树平衡，使用的手段有：左旋和右旋。

右旋（左旋一样的）

左旋，即是逆时针旋转；右旋，即是顺时针旋转。

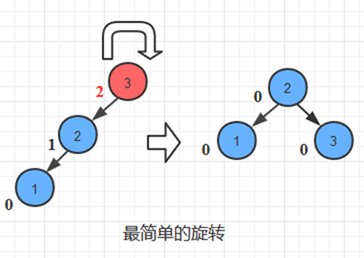
下面是最简单的右旋（下面代码和图片出处）

当然还有这一种情况，其中数字4代表的节点可有可无，无的情况为NULL

下面是旋转的情况

代码应该是

  1 /**
  2    * @description: 右旋方法
  3    */
  4   private Node rotateRight (Node x) {
  5     Node y = x.left; // 取得x的左儿子
  6     x.left = y.right; // 将x左儿子的右儿子（"拖油瓶"结点）链接到旋转后的x的左链接中
  7     y.right = x; // 调转x和它左儿子的父子关系，使x成为它原左儿子的右子树
  8     x.height = max(height(x.left),height(x.right)) + 1; // 更新并维护受影响结点的height
  9     y.height = max(height(y.left),height(y.right)) + 1; // 更新并维护受影响结点的height
 10     return y; // 将y返回
 11   }

其中x为失衡点。而左旋的分析和右旋的情况是一样的。但是一个失衡点有可能是包含了左旋后右旋，或是右旋后左旋。所有下面罗列一下使树平衡会遇到的情况。

四种情况

下面总结来自参考资料

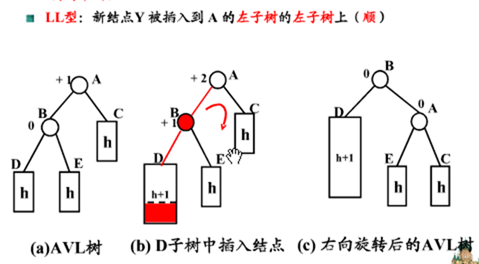
1. 单次右旋： 由于在a的左子树的根结点的左子树上插入结点（LL），使a的平衡因子由1变成2，导致以a为根的子树失去平衡，则需进行一次的向右的顺时针旋转操作

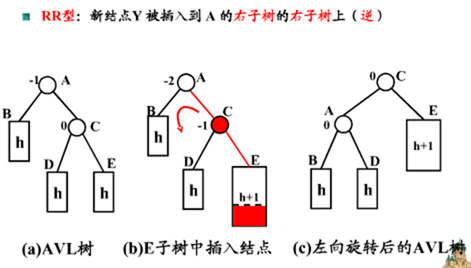
2. 单次左旋： 由于在a的右子树根结点的右子树上插入结点（RR），a的平衡因子由-1变成-2，导致以a为根结点的子树失去平衡，则需要进行一次向左的逆时针旋转操作

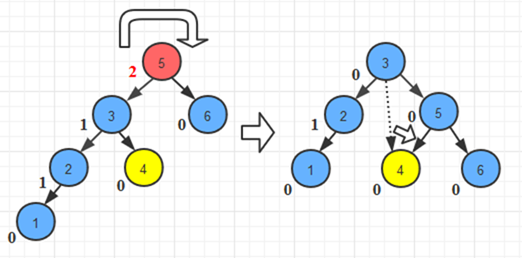
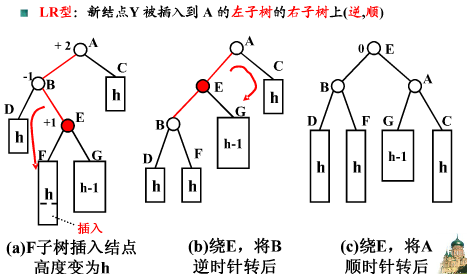
3. 两次旋转、先左旋后右旋： 由于在a的左子树根结点的右子树上插入结点（LR），导致a的平衡因子由1变成2，导致以a为根结点的子树失去平衡，需要进行两次旋转，先左旋后右旋

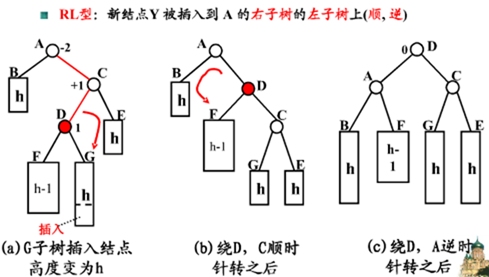
4.两次旋转，先右旋后左旋： 由于在a的右子树根结点的左子树上插入结点（RL）， a的平衡因子由-1变成-2，导致以a为根结点的子树失去平衡，则需要进行两次旋转，先右旋后左旋

那么问题来了，怎么分别判断LL， RR，LR，RL这四种破环平衡的场景呢？

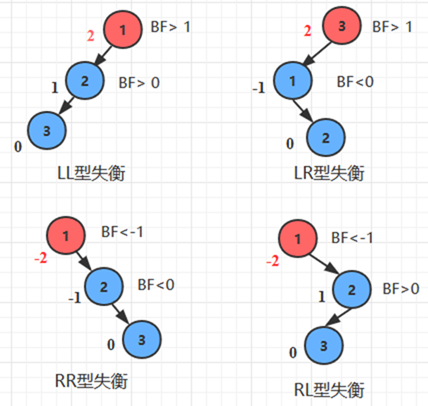
我们可以根据当前破坏平衡的结点的平衡因子，以及其孩子结点的平衡因子来判断，具体如下图所示：

（BF表示平衡因子，最下方的那个结点是新插入的结点）

插入和删除

代码出处见参考资料，非原创

先放出完整代码

  1 package Avl;
  2 
  3 import java.util.LinkedList;
  4 
  5 /**
  6  * @Author: HuWan Peng
  7  * @Date Created in 10:35 2017/12/29
  8  */
  9 public class AVL {
 10   Node root; // 根结点
 11 
 12   private class Node {
 13     int key, val;
 14     Node left, right;
 15     int height = 1; // 每个结点的高度属性
 16 
 17     public Node(int key, int val) {
 18       this.key = key;
 19       this.val = val;
 20     }
 21   }
 22 
 23   /**
 24    * @description: 返回两个数中的最大值
 25    */
 26   private int max(int a, int b) {
 27     return a > b ? a : b;
 28   }
 29 
 30   /**
 31    * @description: 获得当前结点的高度
 32    */
 33   private int height(Node x) {
 34     if (x == null)
 35       return 0;
 36     return x.height;
 37   }
 38 
 39   /**
 40    * @description: 获得平衡因
 41    */
 42   private int getBalance(Node x) {
 43     if (x == null)
 44       return 0;
 45     return height(x.left) - height(x.right);
 46   }
 47 
 48   /**
 49    * @description: 右旋方法
 50    */
 51   private Node rotateRight(Node x) {
 52     Node y = x.left; // 取得x的左儿子
 53     x.left = y.right; // 将x左儿子的右儿子（"拖油瓶"结点）链接到旋转后的x的左链接中
 54     y.right = x; // 调转x和它左儿子的父子关系，使x成为它原左儿子的右子树
 55     x.height = max(height(x.left), height(x.right)) + 1; // 更新并维护受影响结点
 56     y.height = max(height(y.left), height(y.right)) + 1; // 更新并维护受影响结点
 57     return y; // 将y返回
 58   }
 59 
 60   /**
 61    * @description: 左旋方法
 62    */
 63   private Node rotateLeft(Node x) {
 64     Node y = x.right; // 取得x的右儿子
 65     x.right = y.left; // 将x右儿子的左儿子（"拖油瓶"结点）链接到旋转后的x的右链接中
 66     y.left = x; // 调转x和它右儿子的父子关系，使x成为它原右儿子的左子树
 67     x.height = max(height(x.left), height(x.right)) + 1; // 更新并维护受影响结点
 68     y.height = max(height(y.left), height(y.right)) + 1; // 更新并维护受影响结点
 69     return y; // 将y返回
 70   }
 71 
 72   /**
 73    * @description: 平衡 操作
 74    */
 75   private Node reBalance(Node x) {
 76     int balanceFactor = getBalance(x);
 77     if (balanceFactor > 1 && getBalance(x.left) > 0) { // LL型，进行单次右旋
 78       return rotateRight(x);
 79     }
 80     if (balanceFactor > 1 && getBalance(x.left) <= 0) { // LR型 先左旋再右旋
 81       Node t = rotateLeft(x);
 82       return rotateRight(t);
 83     }
 84     if (balanceFactor < -1 && getBalance(x.right) <= 0) {// RR型， 进行单次左旋
 85       return rotateLeft(x);
 86     }
 87     if (balanceFactor < -1 && getBalance(x.right) > 0) {// RL型，先右旋再左旋
 88       Node t = rotateRight(x);
 89       return rotateLeft(t);
 90     }
 91     return x;
 92   }
 93 
 94   /**
 95    * @description: 插入结点（键值对）
 96    */
 97   public Node put(Node x, int key, int val) {
 98     if (x == null)
 99       return new Node(key, val); // 插入键值对
100     if (key < x.key)
101       x.left = put(x.left, key, val); // 向左子树递归插入
102     else if (key > x.key)
103       x.right = put(x.right, key, val); // 向右子树递归插入
104     else
105       x.val = val; // key已存在， 替换val
106 
107     x.height = max(height(x.left), height(x.right)) + 1; // 沿递归路径从下至上更新结点height属性
108     x = reBalance(x); // 沿递归路径从下往上, 检测当前结点是否失衡，若失衡则进行平衡化  
109     return x;
110   }
111 
112   public void put(int key, int val) {
113     root = put(root, key, val);
114   }
115 
116   /**
117    * @description: 返回最小键
118    */
119   private Node min(Node x) {
120     if (x.left == null)
121       return x; // 如果左儿子为空，则当前结点键为最小值，返回
122     return min(x.left); // 如果左儿子不为空，则继续向左递归
123   }
124 
125   public int min() {
126     if (root == null)
127       return -1;
128     return min(root).key;
129   }
130 
131   /**
132    * @description: 删除最小键的结点
133    */
134   public Node deleteMin(Node x) {
135     if (x.left == null)
136       return x.right; // 如果当前结点左儿子空，则将右儿子返回给上一层递归的x.left
137     x.left = deleteMin(x.left);// 向左子树递归， 同时重置搜索路径上每个父结点指向左儿子的链接
138     return x; // 当前结点不是min
139   }
140 
141   public void deleteMin() {
142     root = deleteMin(root);
143   }
144 
145   /**
146    * @description: 删除给定key的键值对
147    */
148   private Node delete(int key, Node x) {
149     if (x == null)
150       return null;
151     if (key < x.key)
152       x.left = delete(key, x.left); // 向左子树查找键为key的结点
153     else if (key > x.key)
154       x.right = delete(key, x.right); // 向右子树查找键为key的结点
155     else {
156       // 结点已经被找到，就是当前的x
157       if (x.left == null)
158         return x.right; // 如果左子树为空，则将右子树赋给父节点的链接
159       if (x.right == null)
160         return x.left; // 如果右子树为空，则将左子树赋给父节点的链接
161       Node inherit = min(x.right); // 取得结点x的继承结点
162       inherit.right = deleteMin(x.right); // 将继承结点从原来位置删除，并重置继承结点右链接
163       inherit.left = x.left; // 重置继承结点左链接
164       x = inherit; // 将x替换为继承结点
165     }
166     if (root == null)
167       return root;
168     x.height = max(height(x.left), height(x.right)) + 1; // 沿递归路径从下至上更新结点height属性
169     x = reBalance(x); // 沿递归路径从下往上, 检测当前结点是否失衡，若失衡则进行平衡化  
170     return x;
171   }
172 
173   public void delete(int key) {
174     root = delete(key, root);
175   }
176 
177 
178   /**
179    * 二叉树层序遍历
180    */
181   private void levelIterator() {
182     LinkedList<Node> queue = new LinkedList<Node>();
183     Node current = null;
184     int childSize = 0;
185     int parentSize = 1;
186     queue.offer(root);
187     while (!queue.isEmpty()) {
188       current = queue.poll();// 出队队头元素并访问
189       System.out.print(current.val + "-->");
190       if (current.left != null)// 如果当前节点的左节点不为空入队
191       {
192         queue.offer(current.left);
193         childSize++;
194       }
195       if (current.right != null)// 如果当前节点的右节点不为空，把右节点入队
196       {
197         queue.offer(current.right);
198         childSize++;
199       }
200       parentSize--;
201       if (parentSize == 0) {
202         parentSize = childSize;
203         childSize = 0;
204         System.out.println("");
205       }
206     }
207   }
208 
209   public void printOutMidNums(){
210 
211   }
212 
213   public static void main(String[] args) {
214     AVL avl = new AVL();
215     avl.put(1, 11);
216     avl.put(2, 22);
217     avl.put(3, 33);
218     avl.put(4, 44);
219     avl.put(5, 55);
220     avl.put(6, 66);
221     avl.levelIterator();
222   }
223 }

插入操作的代码，需要注意的是rotateLeft 或是 rotateRight 方法内部是没有连接上一个父节点的操作的，重连父节点的操作在递归中。

删除操作的解释见 http://www.cnblogs.com/penghuwan/p/8057482.html#_label10，下面引用这篇文章的话来解释删除操作。

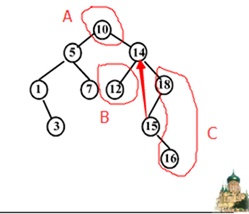
首先介绍 继承结点，继承结点就是某个结点被删除后，能够“继承”某个结点的结点，下面的图片是继承结点的定义

它的作用，用一个例子来说明一下。

相对于14，15是它的继承结点，假若14 被15替换掉，16成为18的左子树节点。那么仍然能保持整颗二叉查找树的有序性。

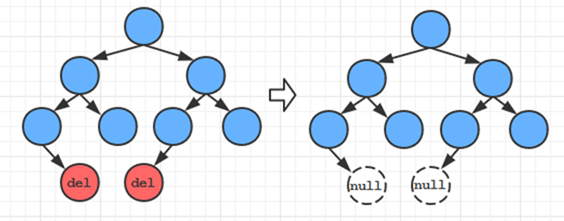
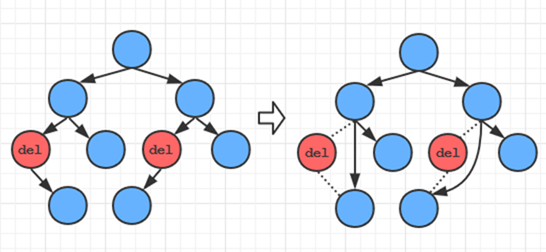
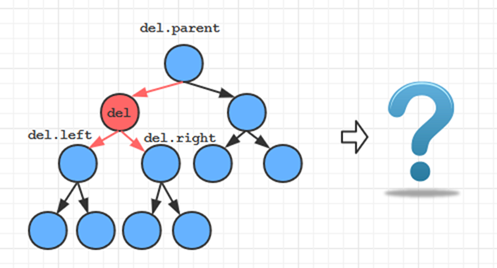
下面说一下删除的三种情况

其中第三种就是使用继承结点的情况。其中需要注意的是，

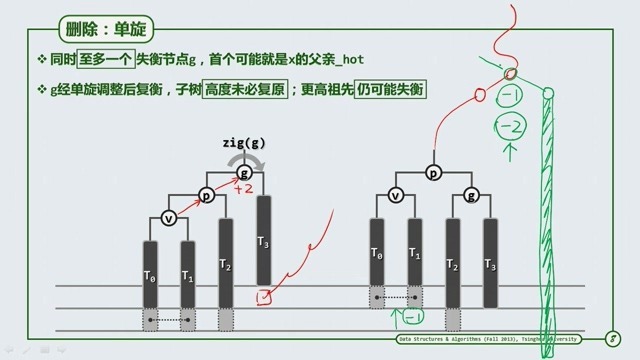
有可能删除操作后，子树的高度 –1 ，而连接子树的上层父节点或是祖父节点因为子树的高度 –1 ，导致继续 rebalance，所以删除操作的最坏情况可以达到 LogN

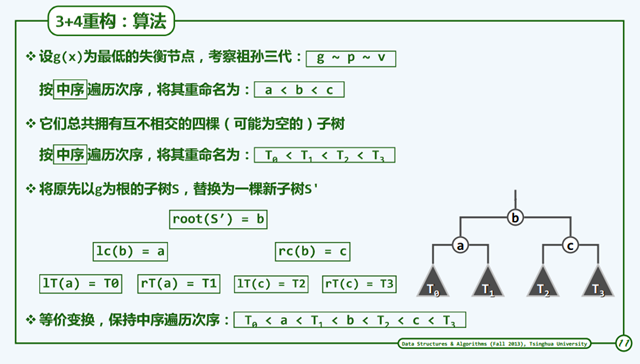
3+4 实现

无论是单旋还是双旋，最终我们可以形成一个稳定的结构，那么我们为何不一开始就拆开而进行拼装形成稳定的结构呢，由于这样

一个结构为三个节点+四个分支，所以我们称为3+4 实现，下面我们看一下使用3+4实现的旋转。（下面的节点RBNode是我在写红黑树

博客一文用到的，同样具有左右子节点，并不影响叙述）

    /**
     * 旋转操作的最终目的使各个节点平衡，旋转只是手段，所以旋转最终调用的是拼接的方法，从而达到目的
     *
     * @return 旋转过后某棵子树的根节点
     */
    public RBNode rotate() {
        RBNode p = this.parent;
        RBNode g = parent.parent;
        if (p.isLChild()) {
            if (this.isLChild()) { //zip-zip
                p.parent = g.parent; //下面操作后根节点变化了，下同
                return connect34(this, p, g, left, right, p.right, g.right);
            } else { // zip-zap
                parent = g.parent; //向上联接
                return connect34(p, this, g, p.left, left, right, g.right);
            }
        } else {
            if (this.isLChild()) { //zag-zip
                v -> parent = g -> parent; //向上联接
                return connect34(g, this, p, g.left, left, right, p.right);
            } else { //zag-zag
                p.parent = g.parent;
                return connect34(g, p, this, g.left, p.left, left, right);
            }
        }
    }

    /**
     * 这个方法进行的操作就是对树的各个节点进行拼接，使用这种方法代替了旋转
     * 无论是这样拼接还是旋转操作，重要的因素是树的中序是不变的
     *
     * @param a  拼接的左节点
     * @param b  拼接的根节点
     * @param c  拼接的右节点
     * @param t0 左节点的子节点
     * @param t1 左节点的子节点
     * @param t2 右节点的子节点
     * @param t3 右节点的子节点
     * @return 返回该树的根节点
     */
    public RBNode connect34(RBNode a, RBNode b, RBNode c, RBNode t0, RBNode t1, RBNode t2, RBNode t3) {
        a.left = t0;
        if (t0 != null) {
            t0.parent = a;
        }
        a.right = t1;
        if (t1 != null) {
            t1.parent = a;
        }
        c.left = t2;
        if (t2 != null) {
            t2.parent = c;
        }
        c.right = t3;
        if (t3 != null) {
            t3.parent = c;
        }
        b.left = a;
        a.parent = b;
        b.right = c;
        b.parent = c;
        return b;
    }

AVL 综合评价

补充

这里推荐一个网站，动态算法的网站：

https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

参考资料

posted @ 2019-01-29 22:07 float123 阅读(10743) 评论(1) 编辑收藏举报

刷新页面返回顶部

Mike-Blog