算法复习——1D/1Ddp优化
搬讲义~~~~
题目1：玩具装箱(bzoj1010)
Description
P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为1…N的N件玩具，第i件玩具经过压缩后变成一维长度为Ci.为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一个容器中，那么容器的长度将为 x=j-i+Sigma(Ck) i<=K<=j 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过L。但他希望费用最小.
Input
第一行输入两个整数N，L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7
Output
输出最小费用
Sample Input
5 4
3
4
2
1
4
3
4
2
1
4
Sample Output
1
经典的决策单调性问题··但也可以用斜率优化····维护一个栈，栈中维护每个决策以及用到它的最优状态的左右区间··每次先更新状态然后将其作为决策二分查找替换栈中决策即可···
另外由于决策单调性是建立在平行四边形不等式的基础上的··而那个东西证起来很麻烦····做题的时候也不容易反应过来··所以尽量还是打表来寻找决策单调性··
代码：
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const int N=5e4+5; long long sum[N],f[N]; struct node { int l,r,pos; }que[N]; int n,L,head,tail; inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } inline long long get(int j,int i) { return f[j]+(long long)(sum[i]-sum[j]+i-j-1-L)*(sum[i]-sum[j]+i-j-1-L); } inline int find(node a,int b) { int le=a.l,ri=a.r; while(le<=ri) { int mid=(le+ri)/2; if(get(b,mid)<get(a.pos,mid)) ri=mid-1; else le=mid+1; } return le; } inline void work() { head=1,tail=0; node temp;temp.l=0,temp.r=n,temp.pos=0;que[++tail]=temp; for(int i=1;i<=n;i++) { while(que[head].r<i) head++; f[i]=get(que[head].pos,i); if(head>tail||get(i,n)<get(que[tail].pos,n)) { while(head<=tail&&(get(i,que[tail].l)<get(que[tail].pos,que[tail].l))) tail--; if(head<=tail) { int t=find(que[tail],i); que[tail].r=t-1; node temp;temp.l=t;temp.r=n;temp.pos=i; que[++tail]=temp; } else { node temp;temp.l=i,temp.r=n,temp.pos=i; que[++tail]=temp; } } } } int main() { //freopen("a.in","r",stdin); n=R();L=R(); for(int i=1;i<=n;i++) sum[i]=R(),sum[i]+=sum[i-1]; work();cout<<f[n]<<endl; return 0; }
题目2：土地购买（bzoj1597）
Description
农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
Input
* 第1行: 一个数: N
* 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽
Output
* 第一行: 最小的可行费用.
Sample Input
4
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.
Sample Output
500
HINT
FJ分3组买这些土地: 第一组:100x1, 第二组1x100, 第三组20x5 和 15x15 plot. 每组的价格分别为100,100,300, 总共500.
这道题首先将土地按x降序排序···可以容易发现那些x和y都会小于某一个土地的土地是肯定是多余无用的···所以将这些点排除后剩余土地肯定是按照x降序··y升序排列的，于是可以推出dp方程
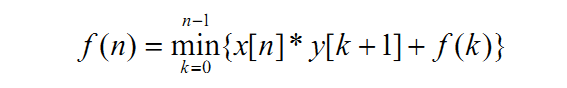
其中f[n]表示的是购买前n块土地的最小花费···方程满足单调性····于是就和上面一道题一样了······其实这道题也可以用斜率优化来做·····后面会提到
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const int N=5e4+5; struct node { int x,y; }a[N],b[N]; struct node1 { int l,r,pos; }que[N]; inline bool cmp(node a,node b) { if(a.x==b.x) return a.y>b.y; return a.x>b.x; } inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } int n,tot; long long f[N]; inline long long calc(int i,int j) { return f[j]+(long long)b[i].y*b[j+1].x; } inline int find(node1 a,int b) { int le=a.l,ri=a.r,ans=a.r+1; while(le<=ri) { int mid=(le+ri)/2; if(calc(mid,b)<calc(mid,a.pos)) ri=mid-1,ans=mid; else le=mid+1; } return ans; } inline bool dp() { int head=1,tail=0; node1 temp;temp.l=0;temp.r=tot;temp.pos=0;que[++tail]=temp; for(int i=1;i<=tot;i++) { while(que[head].r<i) head++; f[i]=calc(i,que[head].pos); if(calc(tot,i)<calc(tot,que[tail].pos)) { while(head<=tail&&calc(que[tail].l,i)<calc(que[tail].l,que[tail].pos)) tail--; if(head<=tail) { int t=find(que[tail],i); que[tail].r=t-1; node1 temp;temp.l=t,temp.r=tot,temp.pos=i;que[++tail]=temp; } else { node1 temp;temp.l=i;temp.r=tot;temp.pos=i;que[++tail]=temp; } } } } int main() { // freopen("a.in","r",stdin); n=R(); for(int i=1;i<=n;i++) a[i].x=R(),a[i].y=R(); sort(a+1,a+n+1,cmp);b[++tot]=a[1];int maxx=a[1].y; for(int i=2;i<=n;i++) if(a[i].y>maxx) maxx=a[i].y,b[++tot]=a[i]; dp();cout<<f[tot]<<endl; return 0; }
题目1：生产产品（vijo1243）
描述
在经过一段时间的经营后，dd_engi的OI商店不满足于从别的供货商那里购买产品放上货架，而要开始自己生产产品了！产品的生产需要M个步骤，每一个步骤都可以在N台机器中的任何一台完成，但生产的步骤必须严格按顺序执行。由于这N台机器的性能不同，它们完成每一个步骤的所需时间也不同。机器i完成第j个步骤的时间为T[i,j]。把半成品从一台机器上搬到另一台机器上也需要一定的时间K。同时，为了保证安全和产品的质量，每台机器最多只能连续完成产品的L个步骤。也就是说，如果有一台机器连续完成了产品的L个步骤，下一个步骤就必须换一台机器来完成。现在，dd_engi的OI商店有史以来的第一个产品就要开始生产了，那么最短需要多长时间呢？
某日Azuki.7对跃动说:这样的题目太简单,我们把题目的范围改一改
对于菜鸟跃动来说,这是个很困难的问题,他希望你能帮他解决这个问题
格式
输入格式
第一行有四个整数M, N, K, L
下面的N行，每行有M个整数。第I+1行的第J个整数为T[J,I]。
输出格式
输出只有一行，表示需要的最短时间。
样例1
样例输入1
3 2 0 2
2 2 3
1 3 1
样例输出1
4
限制
1s
提示
对于50%的数据，N<=5，L<=4，M<=10000
对于100%的数据，N<=5， L<=50000，M<=100000
来源
第一届“OI商店杯” dd_engi原创题目
很妙的一道单调队列的题···,之前其实是做过的···
首先容易想到朴素的dp方程：f[i][j]表示第i个机器生产了第j个过程且前j个过程已经完成生产的最小花费···容易得到：
dp[i][j]=min{dp[k][j']+sum[i][j]-sum[i][j']}+K
其中sum为预处理出的前缀和···j-l<j'<j
由此我们将sum[i][j]提到外面后我们不难发现大括号号中的部分实际上是关于j'的一个函数····因此可以按照上述步骤用单调队列解决：
代码：
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> #include<deque> using namespace std; const int M=1e5+5; const int N=10; const int inf=0x7f7f7f7f; deque<int> dque[N][N]; int n,m,K,sum[M][N],l,dp[M][N]; inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } inline int calc(int i,int k,int j) { return dp[k][j]-sum[k][i]; } int main() { m=R(),n=R(),K=R(),l=R(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) sum[j][i]=R(),sum[j][i]+=sum[j-1][i]; memset(dp,inf,sizeof(dp)); for(int i=1;i<=n;i++) dp[0][i]=0; for(int j=0; j<=m; ++j) { for(int i=1; i<=n; ++i) for(int k=1; k<=n; ++k) if(i!=k) while(!dque[i][k].empty()&&(j-dque[i][k].front())>l) dque[i][k].pop_front(); for(int i=1; i<=n; ++i) for(int k=1; k<=n; ++k) if(i!=k) { int a=0,b=0; if(!dque[i][k].empty()) a=calc(i,dque[i][k].front(),k); b=sum[j][i]+K; dp[j][i]=min(dp[j][i],a+b); } for(int i=1; i<=n; ++i) for(int k=1; k<=n; ++k) if(i!=k) { while(!dque[i][k].empty()&&(calc(i,dque[i][k].back(),k)>=calc(i,j,k))) dque[i][k].pop_back(); dque[i][k].push_back(j); } } int ans=inf; for(int i=1;i<=n;i++) ans=min(ans,dp[m][i]); cout<<ans-K<<endl; return 0; }
题目1:Max Sum Plus Plus(hdu1024)
Problem Description
Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem.
Given a consecutive number sequence S1, S2, S3, S4 ... Sx, ... Sn (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ Sx ≤ 32767). We define a function sum(i, j) = Si + ... + Sj (1 ≤ i ≤ j ≤ n).
Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i1, j1) + sum(i2, j2) + sum(i3, j3) + ... + sum(im, jm) maximal (ix ≤ iy ≤ jx or ix ≤ jy ≤ jx is not allowed).
But I`m lazy, I don't want to write a special-judge module, so you don't have to output m pairs of i and j, just output the maximal summation of sum(ix, jx)(1 ≤ x ≤ m) instead. ^_^
Given a consecutive number sequence S1, S2, S3, S4 ... Sx, ... Sn (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ Sx ≤ 32767). We define a function sum(i, j) = Si + ... + Sj (1 ≤ i ≤ j ≤ n).
Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i1, j1) + sum(i2, j2) + sum(i3, j3) + ... + sum(im, jm) maximal (ix ≤ iy ≤ jx or ix ≤ jy ≤ jx is not allowed).
But I`m lazy, I don't want to write a special-judge module, so you don't have to output m pairs of i and j, just output the maximal summation of sum(ix, jx)(1 ≤ x ≤ m) instead. ^_^
Input
Each test case will begin with two integers m and n, followed by n integers S1, S2, S3 ... Sn.
Process to the end of file.
Process to the end of file.
Output
Output the maximal summation described above in one line.
Sample Input
1 3 1 2 3
2 6 -1 4 -2 3 -2 3
Sample Output
6 8
Hint
Huge input, scanf and dynamic programming is recommended.用f[i][j]表示取了i段且第i段最后一个数取的是num[j]时最大的和···推出朴素dp方程：
f[i][j]=max{f[i][j-1]+num[j],f[i-1][k]+num[j]}
其中k小于j·····
不难发现每当我们先枚举i再枚举j时此时的f[i][j-1]只与上一层i-1有关,所以我们可以降维··用f[j]来代表此时的f[i][j]那么可以推出dp方程
f[j]=max(f[j-1]+num[j],temp[j-1]+num[j]);
其中temp为在枚举i-1时已经处理出的上一层的最小值
代码：
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<string> #include<cstring> #include<algorithm> using namespace std; const int N=1e6+5; const int inf=0x3f3f3f3f; inline int R() { char c;int f=0,i=1; for(c=getchar();(c<'0'||c>'9')&&c!='-';c=getchar()); if(c=='-') i=-1,c=getchar(); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f*i; } int num[N],n,m; long long f[N],temp[N]; int main() { //freopen("a.in","r",stdin); while(scanf("%d%d",&m,&n)!=EOF) { memset(temp,0,sizeof(temp)); memset(f,0,sizeof(f)); for(int i=1;i<=n;i++) num[i]=R(); f[0]=temp[0]=0; for(int i=1;i<=m;i++) { long long maxx=-inf; for(int j=i;j<=n;j++) { f[j]=max(f[j-1]+num[j],temp[j-1]+num[j]); temp[j-1]=maxx;maxx=max(maxx,f[j]); } } long long ans=-inf; for(int i=m;i<=n;i++) ans=max(ans,f[i]); cout<<ans<<endl; } return 0; }
题目2：Max Sum Plus Plus Plus
Problem Description
给定一个由n个正整数组成的整数序列
a1 a2 a3 ... an
求按先后次序在其中取m段长度分别为l1、l2、l3...lm的不交叠的连续整数的和的最大值。
a1 a2 a3 ... an
求按先后次序在其中取m段长度分别为l1、l2、l3...lm的不交叠的连续整数的和的最大值。
Input
第一行是一个整数n(0 ≤ n ≤ 1000)，n = 0表示输入结束
第二行的第一个数是m(1 ≤ m ≤ 20)，
第二行接下来有m个整数l1，l2...lm。
第三行是n个整数a1, a2, a2 ... an.
第二行的第一个数是m(1 ≤ m ≤ 20)，
第二行接下来有m个整数l1，l2...lm。
第三行是n个整数a1, a2, a2 ... an.
Output
输出m段整数和的最大值。
Sample Input
3
2 1 1
1 2 3
4
2 1 2
1 2 3 5
0
Sample Output
5
10
和上面一道题几乎是差不多的···只是注意此时f[i][j]表示的是取第i段,第i段的最后一个数字是num[j]时的最大价值··
#include<iostream> #include<cstdio> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<cctype> #include<cstdlib> #include<algorithm> using namespace std; const int N=1005; const int M=25; int numn[N],numm[M],n,m; long long sumn[N],summ[M],f[N],maxx[N]; inline int R() { char c;int f=0,i=1; for(c=getchar();(c<'0'||c>'9')&&c!='-';c=getchar()); if(c=='-') i=-1,c=getchar(); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f*i; } int main() { //freopen("a.in","r",stdin); while(true) { n=R();if(!n) break;m=R(); memset(sumn,0,sizeof(sumn));memset(summ,0,sizeof(summ)); memset(f,0,sizeof(f));memset(maxx,0,sizeof(maxx)); for(int i=1;i<=m;i++) numm[i]=R(),summ[i]=numm[i]+summ[i-1]; for(int i=1;i<=n;i++) numn[i]=R(),sumn[i]=numn[i]+sumn[i-1]; for(int i=1;i<=m;i++) { for(int j=summ[i];j<=n;j++) { if(j==summ[i]) f[j]=sumn[j]; else f[j]=maxx[j-numm[i]]+sumn[j]-sumn[j-numm[i]]; } for(int j=summ[i];j<=n;j++) { if(j==summ[i]) maxx[j]=f[j]; else maxx[j]=max(maxx[j-1],f[j]); } } long long anss=-1e+18; for(int i=summ[m];i<=n;i++) anss=max(anss,f[i]); cout<<anss<<endl; } return 0; }
