1.学习总结

1.1图的思维导图

1.2 图结构学习体会

  • 深度遍历算法、广度遍历算法：容易理解，便于找寻，比较基础
  • Prim和Kruscal算法：都是从连通图中找出最小生成树的算法。Prim算法直接查找，多次寻找邻边的权重最小值，而Kruskal是需要先对权重排序后查找的，则Kruskal算法效率比Prim快。
  • Dijkstra算法：使用了广度优先搜索解决赋权有向图最短路径问题，以起始点为中心向外层层扩展，直到扩展到终点为止，最终得到一个最短路径
  • 拓扑排序算法：并不一定唯一，要有向图以及判断有没有环路

2.PTA实验作业

2.1 题目1：7-1 图着色问题

2.2 设计思路

将两顶点之间建立一条无向边，c用来标记已经查到不符合条件的边，即有边的两个顶点是同一种颜色，sum来记录该方案中出现的颜色种类。

每一轮都要将f刷为0， if(f[h[j]]==0)查看该种颜色是否是新出现的颜色。

如果c不等于0，说明已经查到不符合条件的边。

如果颜色的种类已经超过k种，说明不可行，不用继续查找；如果查到有不符合条件的边，或者方案中使用的颜色种类不是k中，也说明不可行。

2.3 代码截图

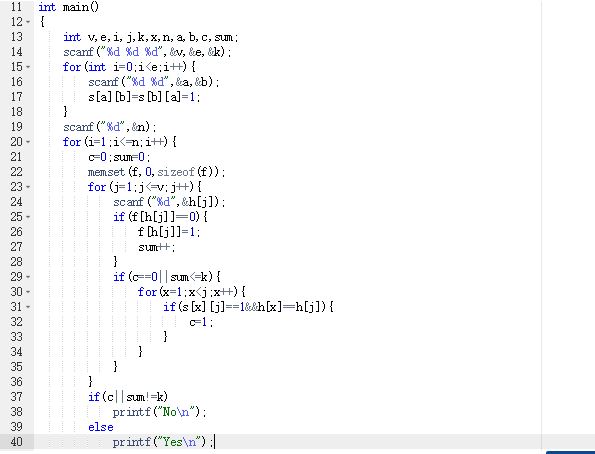
2.4 PTA提交列表说明。

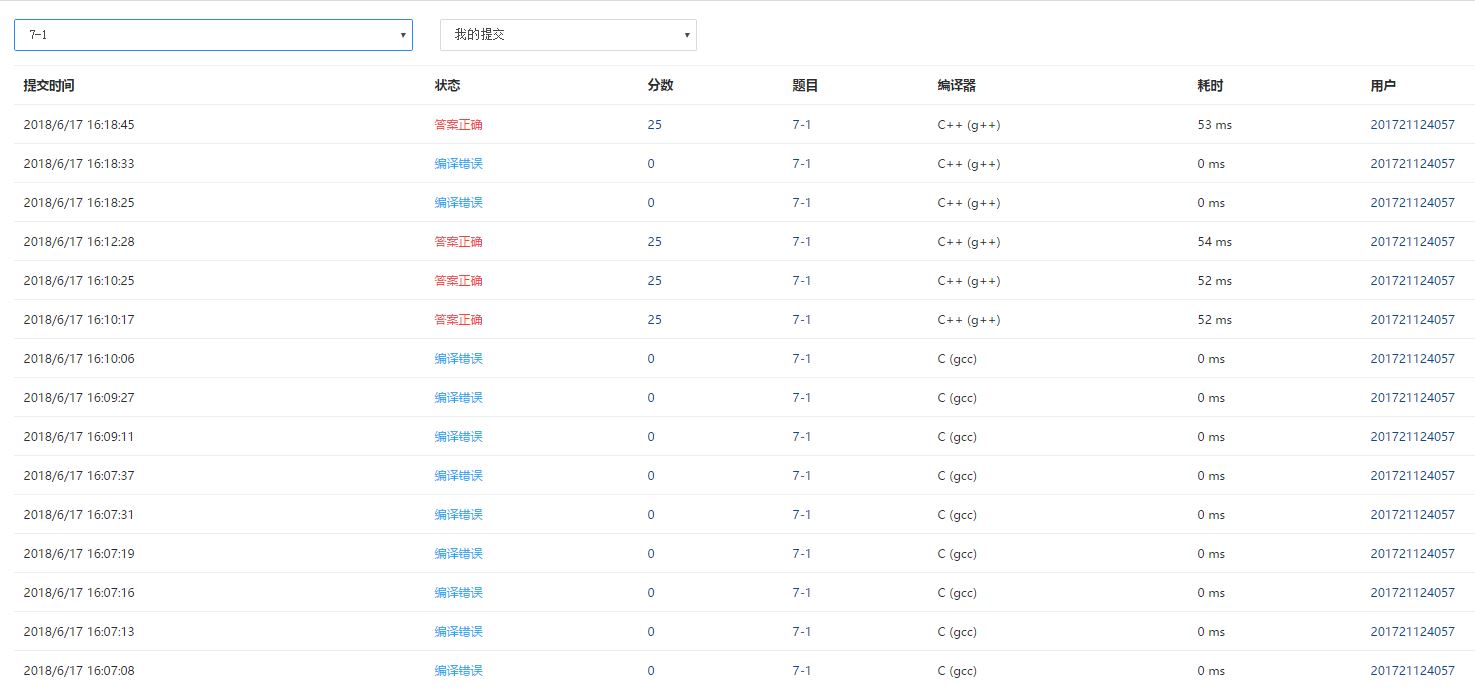
开始只是简单按照题目要求，后来通过借鉴发现按照存在边的两点的颜色不能是同一种颜色以及每一种着色方案使用的颜色个数要正好是k种这两个条件就可以解决问题，于是才答案正确。PTA提交时开始有一处未加分号导致编译错误，后未选用C++导致编译错误，改正后正确。

2.1 题目2：题目名称

2.2 设计思路

先创建find函数来寻找一个点的最后一个节点，如果没到最后一个，就往下一个寻找；

创建add合并函数，用来对自己的下一个点赋值；

最后使用main函数进行判断和输出。

2.3 代码截图

2.4 PTA提交列表说明。

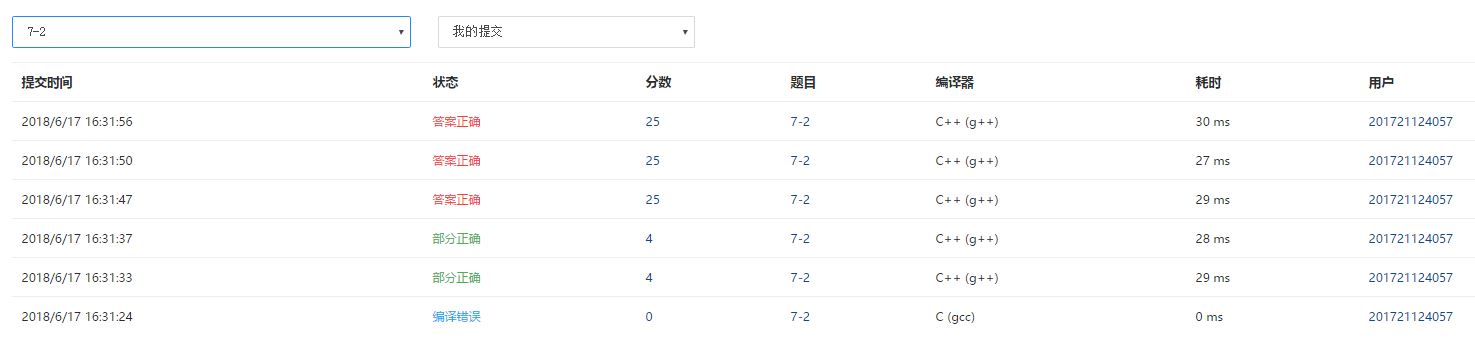
本题较难，最开始使用二维数组进行编写，得出代码复杂，改错困难，后和同学商讨后发现要用并查集的方法，于是上网借鉴代码理解后写出正确代码。

2.1 题目3：7-4 公路村村通

2.2 设计思路

建立cmp和find函数联通并查集，n个村庄可修n-1条路，用kruskal算法找最小生成树 ，最后用main得出结果。

2.3 代码截图

2.4 PTA提交列表说明。

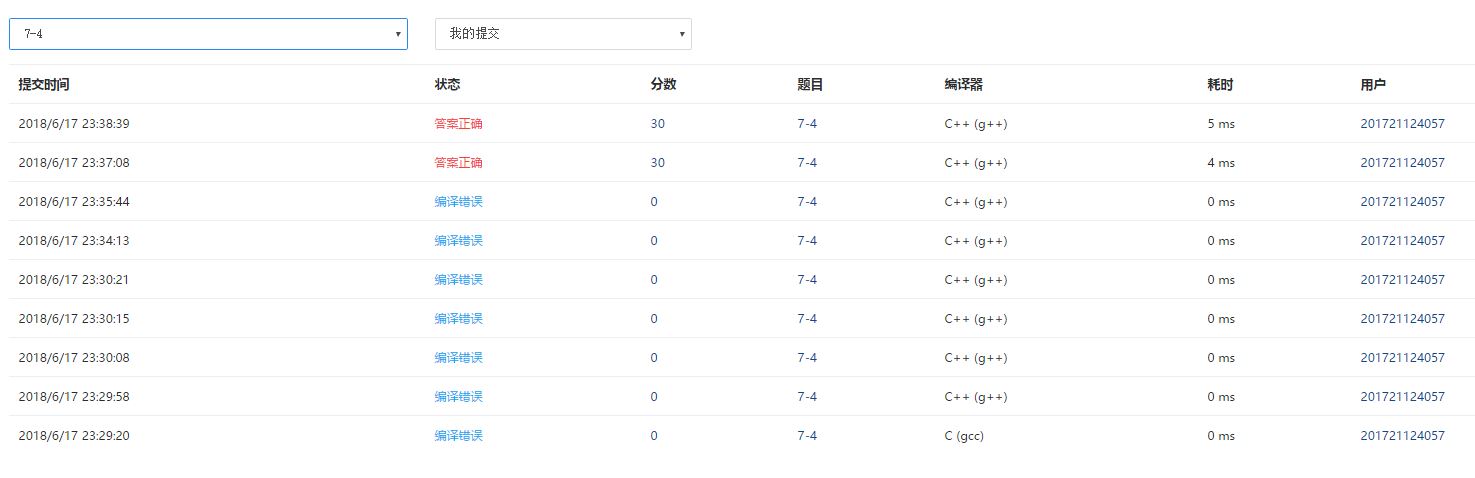
开始使用prime算法，但由于对知识不熟练导致程序无法正常得出结果，后参考后得以成功运行。之后借鉴较高效的Kruscal算法，同样得出正确结果。

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的总分：

4. 阅读代码

　　7-9 天梯地图

  1. #include <cstdio>  
  2. #include <algorithm>  
  3. #include <vector>  
  4. using namespace std;  
  5. const int inf = 999999999;  
  6. int dis[510], Time[510], e[510][510], w[510][510], Timepre[510], weight[510];  
  7. bool visit[510];  
  8. vector<int> Timepath, dispath, temppath, dispre[510];  
  9. int st, fin, minnode = inf;  
  10. void dfsTimepath(int v) {  
  11.     Timepath.push_back(v);  
  12.     if(v == st) {  
  13.         return ;  
  14.     }  
  15.     dfsTimepath(Timepre[v]);  
  16. }  
  17.   
  18. void dfsdispath(int v) {  
  19.     temppath.push_back(v);  
  20.     if(v == st) {  
  21.         if(temppath.size() < minnode) {  
  22.             minnode = temppath.size();  
  23.             dispath = temppath;  
  24.         }  
  25.         temppath.pop_back();  
  26.         return ;  
  27.     }  
  28.     for(int i = 0; i < dispre[v].size(); i++) {  
  29.         dfsdispath(dispre[v][i]);  
  30.     }  
  31.     temppath.pop_back();  
  32. }  
  33. int main() {  
  34.     fill(dis, dis + 510, inf);  
  35.     fill(Time, Time + 510, inf);  
  36.     fill(weight, weight + 510, inf);  
  37.     fill(e[0], e[0] + 510 * 510, inf);  
  38.     fill(w[0], w[0] + 510 * 510, inf);  
  39.     int n, m;  
  40.     scanf("%d %d", &n, &m);  
  41.     int a, b, flag, len, t;  
  42.     for(int i = 0; i < m; i++) {  
  43.         scanf("%d %d %d %d %d", &a, &b, &flag, &len, &t);  
  44.         e[a][b] = len;  
  45.         w[a][b] = t;  
  46.         if(flag != 1) {  
  47.             e[b][a] = len;  
  48.             w[b][a] = t;  
  49.         }  
  50.     }  
  51.     scanf("%d %d", &st, &fin);  
  52.   
  53.     Time[st] = 0;  
  54.     for(int i = 0; i < n; i++) {  
  55.         Timepre[i] = i;  
  56.     }  
  57.     for(int i = 0; i < n; i++) {  
  58.         int u = -1, minn = inf;  
  59.         for(int j = 0; j < n; j++) {  
  60.             if(visit[j] == false && Time[j] < minn) {  
  61.                 u = j;  
  62.                 minn = Time[j];  
  63.             }  
  64.         }  
  65.         if(u == -1) break;  
  66.         visit[u] = true;  
  67.         for(int v = 0; v < n; v++) {  
  68.             if(visit[v] == false && w[u][v] != inf) {  
  69.                 if(w[u][v] + Time[u] < Time[v]) {  
  70.                     Time[v] = w[u][v] + Time[u];  
  71.                     Timepre[v] = u;  
  72.                     weight[v] = weight[u] + e[u][v];  
  73.                 } else if(w[u][v] + Time[u] == Time[v] && weight[v] > weight[u] + e[u][v]) {  
  74.                     weight[v] = weight[u] + e[u][v];  
  75.                     Timepre[v] = u;  
  76.                 }  
  77.             }  
  78.         }  
  79.     }  
  80.     dfsTimepath(fin);  
  81.   
  82.     fill(visit, visit + 510, false);  
  83.     dis[st] = 0;  
  84.     for(int i = 0; i < n; i++) {  
  85.         int u = -1, minn = inf;  
  86.         for(int j = 0; j < n; j++) {  
  87.             if(visit[j] == false && minn > dis[j]) {  
  88.                 u = j;  
  89.                 minn = dis[j];  
  90.             }  
  91.         }  
  92.         if(u == -1) break;  
  93.         visit[u] = true;  
  94.         for(int v = 0; v < n; v++) {  
  95.             if(visit[v] == false && e[u][v] != inf) {  
  96.                 if(e[u][v] + dis[u] < dis[v]) {  
  97.                     dis[v] = e[u][v] + dis[u];  
  98.                     dispre[v].clear();  
  99.                     dispre[v].push_back(u);  
  100.                 } else if(e[u][v] + dis[u] == dis[v]) {  
  101.                     dispre[v].push_back(u);  
  102.                 }  
  103.             }  
  104.         }  
  105.     }  
  106.     dfsdispath(fin);  
  107.     printf("Time = %d", Time[fin]);  
  108.     if(dispath == Timepath) {  
  109.         printf("; Distance = %d: ", dis[fin]);  
  110.     } else {  
  111.         printf(": ");  
  112.         for(int i = Timepath.size() - 1; i >= 0; i--) {  
  113.             printf("%d", Timepath[i]);  
  114.             if(i != 0) printf(" => ");  
  115.         }  
  116.         printf("\n");  
  117.         printf("Distance = %d: ", dis[fin]);  
  118.     }  
  119.     for(int i = dispath.size() - 1; i >= 0; i--) {  
  120.         printf("%d", dispath[i]);  
  121.         if(i != 0) printf(" => ");  
  122.     }  
  123.     return 0;  
  124. }  

　　用两个Dijkstra + DFS。一个求最快路径（如果相同求路径的那条），一个求最短路径（如果相同求结点数最小的那条）。求最快路径可以直接在Dijkstra里面求前驱结点Timepre数组。求最短路径因为要求结点数最小的那条，所以要用dispre的二维数组存储所有结点的最短路径，然后用DFS求出满足条件的结点数最小的那条。