主元分析（PCA）在计算机图形学中的应用

    本文首先简要介绍主元分析，然后侧重于举例说明主元分析在计算机图形学中的应用，最后给出主元分析的计算步骤与其作用于三维数据的相应代码。

一. 简介

    主元分析，即Principal Component Analysis，简称PCA，是一种对数据进行分析的技术。如其名字所述，它的作用是分析数据分布的主要元素/结构。主元分析会由主到次找到数据的分布方向，通过舍去那些次要的分布方向，它可以用于去除噪声、数据降维等。其计算简单，在多个领域有着广泛的应用。

    以二维平面数据可以形象地说明主元分析。如图 1所示，给定XA、YA坐标系下的一些2维数据点（图中圆圈），我们希望找到方向轴Xp、Yp，其中Xp代表了数据的主要分布方向（主元轴），当Yp方向的变化很小时，我们可以认为Yp方向的变化为噪声所产生，因此可以去掉Yp这一维。

图 1 主元分析示意图

    设图1中原来的有一个数据P为（3.05, 2.95），即

    主元分析获得主元轴Xp、Yp后，P可以表示为

     此时P仍为2维数据，但是因为Xp轴的存在，只用一个坐标4.184表示就可以了。

    教程“A tutorial on Principal Components Analysis, Lindsay I Smith”给出了十分浅显易懂的主元分析推理，你可以在本文附件中获得此教程，同时本文附件中的代码实现了该教程的方法（教程中的代码仅限于对三维数据的分析）。

二. 主元分析在图形学中的应用

    在此举出本人在计算机图形学领域利用PCA的几个地方:

1. 通过降维找出一堆顶点数据的分布特征（或者说模式pattern）：分析网格数据（如对人物的网格进行分析从而发现其骨架拓扑）时，有时会得到一堆散乱分布在关节附近的顶点数据，利用主元分析对这些散乱的顶点进行降维，如从3维降到2维，则可以发现这些顶点数据的分布特征。
   如图 2所示，图 2a在3ds Max中以Top、Front、Left、Perspective视角显示了原数据，图 2b中的蓝色线条表示主元分析得到的前两个主元轴，去掉最不重要的一个轴后，点数据表示在两个主元轴下，可看出此时数据更好的呈现出了圆环分布的特征。
   
   
2. 求给定三角形网格的有向包围盒（OBB）。OBB是一种对模型进行视锥裁剪与碰撞检测的有效方式，然而通常网格模型表示在一个与世界坐标系平行的框架中，可以利用主元分析求得模型所在的各个自然轴，如一个斜放着的圆柱其第一个自然轴是有圆柱底面中心指向圆柱顶面中心的方向。求得各个自然轴后，通过各顶点坐标与单位自然轴的点积，即可获得各顶点在自然轴上的分布范围，进而得到OBB。
   
   
3. 对人物动画进行特征提取。例如数据捕捉采集到的人体步行动画通常由不同时刻各个关节（约40~60个）的角度来表示，当数据量很大时，对数据的存储与处理都是一件耗费资源的事情。而普通的步行动作中，当一个人左臂向前摆动时右臂总向后摆动，这就是说这些数据有耦合，从而可以利用主元分析进行特征提取与压缩。由此也可以想象得到主元分析另一个强大的地方：对于一些高维度的数据，很难用三维图形的方式去展现，因此很难观察出其分布特征，而主元分析计算则可以发现这些特征。

a 原始数据

b 主元分析后的数据

图 2 三维点数据降维

三. 主元分析计算步骤与代码

    那么如何进行主元分析呢，教程“A tutorial on Principal Components Analysis》，Lindsay I Smith”已经给出了近乎于完美的讲解，在此，本人列出其计算步骤（以m维数据为例）：

1. 获取数据 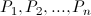 （每一个数据为一个m维列向量）
2. 求出数据平均值 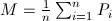，并用原数据减去均值得到
3. 计算协方差矩阵
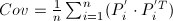
4. 计算协方差矩阵的特征值 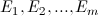与特征向量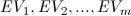 （特征值与特征向量成对出现）。
5. 由大到小依次排列特征值得 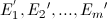，对应特征向量为 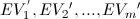。特征向量代表了原数据的分布方向，其对应的特征值越大，则该向量越重要（即为主元）；其对应的特征值越小，则该向量越次要。

    此时即可根据特征值的大小来决定取舍了。如一个特征值为10，而另一个特征值为0.1，在说明这两个分布差了100倍，通常我们会舍弃特征值为0.1的方向的那个维度，因此就可以对数据进行降维表示了。例如我们取了前k个特征值，则就可以将数据表示在以前K个特征向量为基轴的坐标系下了。

 

    你可以在这里下载本文C++代码。

    代码以SampleData.txt中的三维数据点作为输入，程序的输出存放在Results目录，

    输出的目录中包括3个文件：

1. PCAResult.txt 存放经主元分析后在主元轴坐标系下的数据坐标。
2. DisplaySamples.ms 为3ds Max脚本文件，用3ds Max打开后可看到SampleData.txt表示的数据点。
3. DisplayResult.ms 为3ds Max脚本文件，用3ds Max打开后可看到将原3维数据在主元轴坐标系下降到2维后的数据点；同时该文件还显示了主元分析得到的前两个主元轴。

   更加通用的pca代码（Matlab代码）在这里下载。