Problem Description
Function Fx,ysatisfies:

For given integers N and M,calculate Fm,1 modulo 1e9+7.
 

 

Input
There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
 

 

Output
For each given N and M,print the answer in a single line.
 

 

Sample Input
2
2 2
3 3
 

 

Sample Output
2
33

 

数学题，反正我不会。。。数学基础太差了，直接用大佬的数学公式写的

参考博客：http://www.cnblogs.com/Just--Do--It/p/7248089.html

主要是学到了取余和除的话需要求逆元！！可以用费马小定理求，目前我只会这个

继续加油！

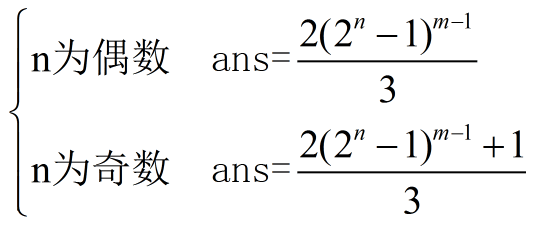
 1 #include<cstdio>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<string.h>
 5 #include<cmath>
 6 #include<math.h>
 7 using namespace std;
 8 
 9 #define MOD 1000000000+7
10 
11 long long quick_mod(long long a,long long b)//快速幂，复杂度log2n
12 {
13     long long ans=1;
14     while(b)
15     {
16         if(b&1)
17         {
18             ans*=a;
19             ans%=MOD;
20             b--;
21         }
22         b/=2;
23         a*=a;
24         a%=MOD;
25     }
26     return ans;
27 }
28 
29 long long inv(long long x)
30 {
31     return quick_mod(x,MOD-2);//根据费马小定理求逆元，3*（3^(mod-2)）=1
32 }
33 
34 int main()
35 {
36     int T;
37     scanf("%d",&T);
38     long long n,m,ans;
39     while(T--)
40     {
41         scanf("%lld%lld",&n,&m);
42         if(n%2==0)
43             ans=(quick_mod(quick_mod(2,n)-1,m-1)*2)*inv(3);
44         else
45             ans=(quick_mod(quick_mod(2,n)-1,m-1)*2+1)*inv(3);
46         ans%=MOD;
47         printf("%lld\n",ans);
48     }
49     return true;
50 }