寒假作业2
问题
一栋10层的大楼(楼层编号1-10),设有一台无限载重的电梯,初始时电梯停在1层。电梯移动1层的耗时为1,在某一层停靠的耗时为1(时间初始为0)。为了使得乘客等待的时间(电梯在目的层的停靠时刻 - 乘客发出请求时刻)总和最小,请你编写一个程序来进行电梯调度。
输入有5个请求,每个请求一行,格式为请求时刻 起始楼层数 去往方向,其中方向为0代表向上去往10层,为1代表向下去往1层。
输出每次对应的决策,每一行的输出格式为xx时,停靠在x楼。其中,“xx时刻”指的是在某层楼停靠的时刻,且不算入在该层的停靠时间。如:
当0时刻时,电梯此时在1层,输入有0 1 0,那么电梯从1层接客(1s)前往10层(9s),应输出10时,停靠在10楼(1+9=10)。此时,该乘客等待时间为(10-0=)10。
当0时刻,电梯此时在1层,输入有0 2 0,那么电梯从1层前往2层(1s),接上乘客(1s),前往10层(8s),应输出10时,停靠在10楼(1+1+8=10)。此时,该乘客等待时间为(10-0=)10s。
最后输出完成5个请求(所有乘客都到达目的地)后,各乘客的等待时间总和。
请自己设计5组测试用例,且具有一定代表性,用以验证程序是否是最小耗时。
思考过程
提示:本文针对的是我对这题的思考过程,思路不止一种。
我刚看题的时候首先先想了一下现实生活中电梯的运行模式,毕竟这种题目是比较现实的。在现实中如果乘客没有发出请求,电梯是不知道有这一条指令的,即电梯是没有未卜先知的能力的。但是当电梯收到指令后,电梯便知道了当前已经收到的所有指令,即可以把问题看成,电梯在收到新的指令时所在的位置完成目前已知的所有指令的最短时间,即电梯“未卜先知”,则一定至少存在一个“最优解”。而电梯没有继续收到新的指令时,就按现行路线一直执行下去。
因此,本题其实并不够完善。根据我对现实中电梯的理解和自己的想法,加入下列条件和定义
电梯不具备未卜先知的能力,即电梯在没有指令可以执行时只能原地不动
电梯可以掉头
指令确定的条件下,一定存在至少一个当前的最优解运行顺序
当得到新的指令时,最优平衡被打破,需要重新计算运行最优顺序
每当得到新的请求时,若电梯正在运行,无非几种状态需要判断
要不要停下?/要不要返回?
方向如何?
因此,电梯的运行会分为以下几个分支
1、继续运行
2、停靠接人,并按原方向继续运行
3、停靠接人,反方向运行
在没有新乘客的请求时,电梯是无法预知是否有下一个请求的,因此我们就去预估所有当前未完成指令3种状态各自完成所有请求的时间,并作为当前最优的路线。
不过,这种贪心的思路非常复杂,针对的策略非常的多,就我上面浅显的分析策略显然只能针对一位乘客的情况,当指令数量增加时,问题就不止这3个分支了。
在思考很久以后,我想到了另外一种思路。把电梯看成只有运行和停靠两个动作,针对本题仅5条指令的数据大小,那么可以暴力搜索停靠点的顺序来确定电梯在每个停靠点的停下的顺序。针对上面分析的未收到请求时电梯只会按照当前最优解运行,那么电梯在收到请求时重新分析下一步,而电梯只要往下一步方向运行,等到当前目标执行结束后,由于数据较小,可以重新分析并规划下一步的目标。当然,其实再多花一点空间(还有现实中实现代码的时间)可以固定电梯的运行顺序,避免重复的运算,达到进一步减少时间复杂度的效果。
代码概览
代码名 | 长度 | bug数量
- | :-: | -:
A.cpp | 169行 | 11个
执行数据
注:部分执行数据参考@Stolf
先上两个最简单的数据

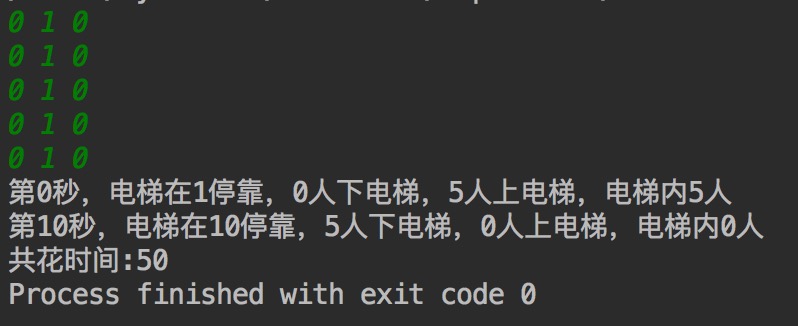
看样子没有问题
然后是比较复杂的数据

与Stolf的运行结果一致,手算也没有问题,程序按着正确的运行顺序运行
接下来是一个时间跨度比较长的例子,当没有请求时,电梯应处于静止状态

手算结果:10+22+26+16+6 = 80秒,与计算结果一致
第5个例子,电梯:我有句mmp不知当讲不当讲

收获
第一次摆脱固定结果的小程序去实现这种自由度非常高的工程,确实感受到了非常大的压力和难度,特别是没有想清楚就去实现,小程序几十行推掉重来即可,但是这种上百行的代码不经过细细的思考就去写确实非常的短见。推掉重构好几次后确实吃足了教训,但是百行代码完成后的欣喜也是第一次尝到,还是很值得的。
Pintia小作业