树的顺序遍历的应用
树的顺序遍历分为先序遍历、中序遍历、后序遍历三种(如果没有了解过,请参见此处)
上次已经说过,有关树的顺序遍历的题目还是有点思维难度的,我们先来看一下
题目链接A
加分二叉树
题目描述 Description
设一个n个节点的二叉树tree的中序遍历为(l,2,3,…,n),其中数字1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第j个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分× subtree的右子树的加分+subtree的根的分数
若某个子树为主,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空
子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出;
(1)tree的最高加分
(2)tree的前序遍历
现在,请你帮助你的好朋友XZ设计一个程序,求得正确的答案。
输入描述 Input Description
第1行:一个整数n(n<=30),为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(分数<=100)
输出描述 Output Description
第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。
第2行:n个用空格隔开的整数,为该树的前序遍历。
样例输入 Sample Input
5
5 7 1 2 10
样例输出 Sample Output
145
3 1 2 4 5
数据范围及提示 Data Size & Hint
n(n<=30)
分数<=100
这道题特殊的地方在于它没有给定树的结构,而是要你求出这棵树的结构
但我们可以发现,这棵树的中序遍历一定满足from 1 to n,所以我们回想起中序遍历的性质:
在中序遍历下,某棵子树(在该子树范围内)的左边的一定是他的左子树,右边的一定是它的右子树
即,在这道题中:分数=左边合并的分数*右边合并的分数+此根节点的的分数
于是,这道题便可以用区间合并做了,Dp方程为:
$$ dp[i][j]=dp[i][k-1]*dp[k+1][j]+a[k] (i<k<j) $$
那么第二问呢?
此时,我们可以考虑新开一个数组g[i][j]表示合并区间[i,j]时,使得其得分最大的根节点的编号(枚举实现)
$$ if(dp[i][j]<dp[i][k-1]*dp[k+1][j]+a[k] (i<k<j)) $$
$$ \ \ \ g[i][j]=k $$
输出的时候,再按照前序遍历的规则输出
void Out(int fa){
printf("%d ",fa);
Out(lson);
Out(rson);
}
上代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int maxn=35;
int a[maxn],n;
int dp[maxn][maxn];
int tr[maxn],rt,ans[maxn][maxn],imax;
int read(){
int Value=0,Base=1;char Ch=getchar();
for(;!isdigit(Ch);Ch=getchar())if(Ch=='-')Base=-1;
for(;isdigit(Ch);Ch=getchar())Value=Value*10+(Ch^'0');
return Value*Base;
}
void Out(int l,int r){
if(l>r)return ;
printf("%d ",ans[l][r]);
if(ans[l][r]!=l)Out(l,ans[l][r]-1);
if(ans[l][r]!=r)Out(ans[l][r]+1,r);
}
int main( ){
int m,j,k,i;
n=read();
for(i=0;i<=2*n;i++)
for(j=0;j<=2*n;j++)
dp[i][j]=1;
for(i=1;i<=n;i++)a[i]=read(),dp[i][i]=a[i],ans[i][i]=i;
for(i=n;i>=1;i--){
for(j=i+1;j<=n;j++){
for(k=i;k<=j;k++){
if(dp[i][j]<dp[i][k-1]*dp[k+1][j]+a[k]){
dp[i][j]=dp[i][k-1]*dp[k+1][j]+a[k];
ans[i][j]=k;
}
}
}
}
printf("%d\n",dp[1][n]);
Out(1,n);
puts("");
return 0;
}
现在,如果一下子就AC了,就可以睡觉了就来看看B题吧
题目链接B
树的遍历
题目描述 Description
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
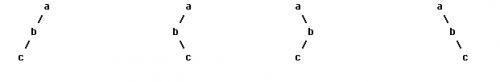
所有这些二叉树都有着相同的前序遍历和后序遍历,但中序遍历却不相同。
输入描述 Input Description
输入文件共2行,第一行表示该树的前序遍历结果,第二行表示该树的后序遍历结果。输入的字符集合为{a-z},长度不超过26。
输出描述 Output Description
输出文件只包含一个不超过长整型的整数,表示可能的中序遍历序列的总数。
样例输入 Sample Input
abc
cba
样例输出 Sample Output
4
数据范围及提示 Data Size & Hint
如描述
这道题看似没有任何思路啊~不过其实是结论题,各位可以再想一想
~
~
~
经过观察,可以发现,当某棵树某个节点只有一个儿子时,才有可能出现先序遍历和后序遍历都相同,而中序遍历不同的情况
例如:
A
/ \
B D
/
C
如果B节点的左儿子C接在右儿子的位置上,那么先序遍历和后序遍历都不会变,但会影响中序遍历
所以,每有一对这样的节点,ans就要乘以2,这种情况的表现就是先序遍历中有一对紧邻着的AB,而在后序遍历中是BA
看代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
char a[maxn],b[maxn];
int ans=0;
int main( ){
int m,n,j,k=1,i;
scanf("%s%s",a,b);
for(i=0;i<strlen(a);i++)
for(j=1;j<strlen(b);j++)
if(a[i]==b[j] && a[i+1]==b[j-1])
ans++;
for(i=1;i<=ans;i++)k<<=1;
printf("%d\n",k);
}
那么关于树的顺序遍历的内容就是这些了~



