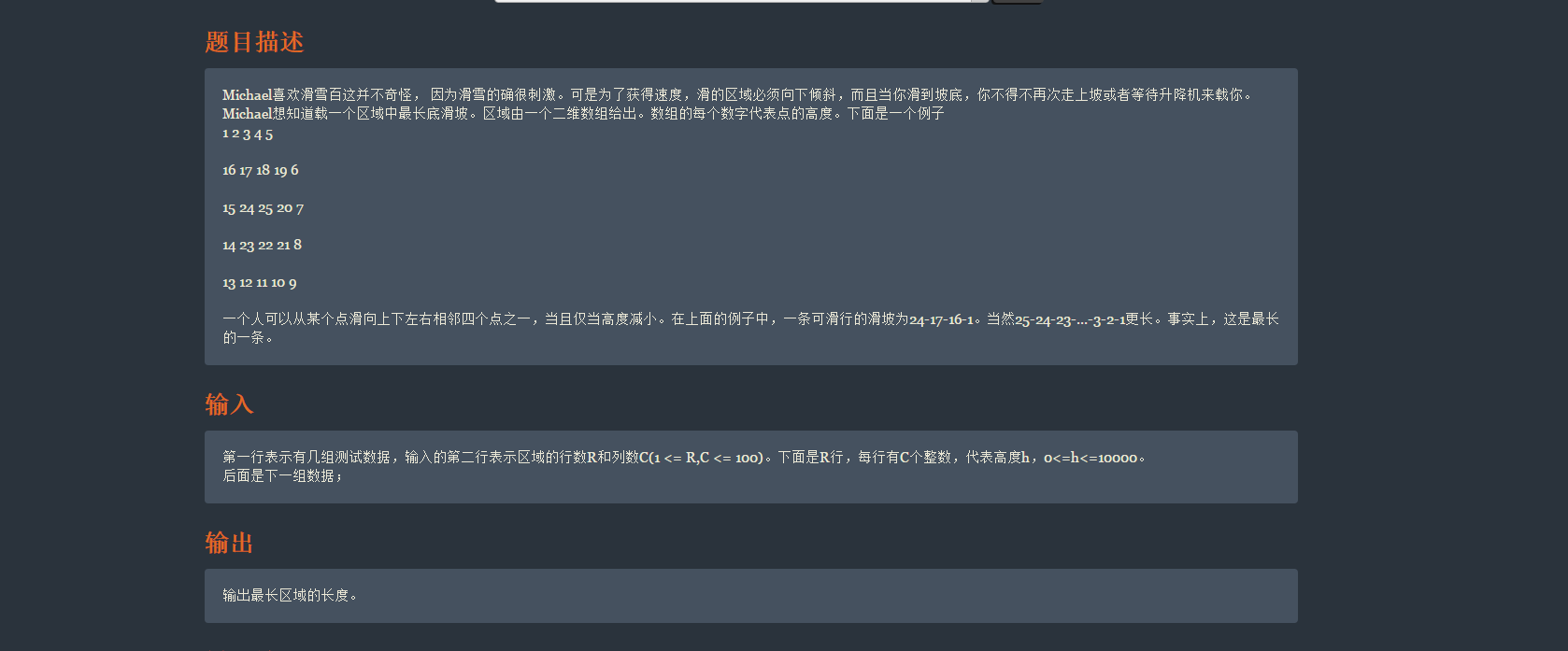

我的代码上去就是 直接纯粹的 暴力 . 居然没有超时 200ms 可能数据比较小 一会在优化
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<limits.h>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<string>
#include<sstream>
#include<map>
#include<cctype>
using namespace std;
int n,m,a[105][105],visited[105][105],b[4][2]={0,-1,0,1,-1,0,1,0},minn;
void DFS(int y,int x,int now)
{
for(int i=0;i<4;i++)
{
int x1=x+b[i][1],y1=y+b[i][0];
if(x1>=0&&x1<m&&y1>=0&&y1<n&&!visited[y1][x1]&&a[y1][x1]<a[y][x])
{
now++;
if(now>minn)
minn=now;
visited[y1][x1]=1;
DFS(y1,x1,now);
visited[y1][x1]=0;
now--;
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&m,&n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&a[i][j]);
minn=1;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
memset(visited,0,sizeof(visited));
visited[i][j]=1;
DFS(i,j,1);
}
printf("%d\n",minn);
}
}
下面附上 动态规划的 解法 这个 动态规划 是一种 人人为我 , 的思想 , 先根据 高度进行从小到的 排序 然后 然后从 第二小的 开始 检查 周围是否 有比他 还小的 , 如果有的话 , 将周围的 +1 个 自身相比 取最大值 , 废话少说 放码过来
1 #include<stdio.h>
2 #include<string.h>
3 #include<math.h>
4 #include<iostream>
5 #include<limits.h>
6 #include<algorithm>
7 #include<queue>
8 #include<vector>
9 #include<set>
10 #include<stack>
11 #include<string>
12 #include<sstream>
13 #include<map>
14 #include<cctype>
15 using namespace std;
16 struct node
17 {
18 int x,y,h;
19 }a[10005];
20 bool cmp(node example_a,node example_b)
21 {
22 return example_a.h<example_b.h;
23 }
24 int b[4][2]={0,-1,0,1,-1,0,1,0},c[105][105],d[105][105];
25 int main()
26 {
27 int t;
28 scanf("%d",&t);
29 while(t--)
30 {
31 int n,m;
32 scanf("%d%d",&n,&m);
33 int total=0;
34 for(int i=0;i<n;i++)
35 {
36 for(int j=0;j<m;j++)
37 {
38 d[i][j]=1;
39 scanf("%d",&c[i][j]);
40 a[total].h=c[i][j],a[total].x=j,a[total].y=i; // 将所有的 长度 默认为 1
41 total++;
42 }
43 }
44 sort(a,a+total,cmp);
45 int maxn=1;
46 for(int i=1;i<total;i++) // 从 第二小的 开始 当周围 有 比他小 的 就 +1
47 {
48 for(int j=0;j<4;j++)
49 {
50 if(a[i].x+b[j][1]>=0&&a[i].x+b[j][1]<m&&a[i].y+b[j][0]>=0&&a[i].y+b[j][0]<n&&c[a[i].y][a[i].x]>c[a[i].y+b[j][0]][a[i].x+b[j][1]])
51 {
52 d[a[i].y][a[i].x]=max(d[a[i].y][a[i].x],d[a[i].y+b[j][0]][a[i].x+b[j][1]]+1);
53 maxn=max(maxn,d[a[i].y][a[i].x]);
54 }
55 }
56 }
57 printf("%d\n",maxn);
58 }
59 return 0;
60 }





