稀疏自动编码之反向传播算法(BP)
假设给定m个训练样本的训练集![]() ,用梯度下降法训练一个神经网络,对于单个训练样本(x,y),定义该样本的损失函数:
,用梯度下降法训练一个神经网络,对于单个训练样本(x,y),定义该样本的损失函数:
![]()
那么整个训练集的损失函数定义如下:
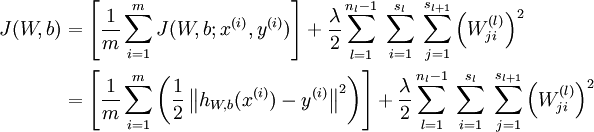
第一项是所有样本的方差的均值。第二项是一个归一化项(也叫权重衰减项),该项是为了减少权连接权重的更新速度,防止过拟合。
我们的目标是最小化关于 W 和 b 的函数J(W,b). 为了训练神经网络,把每个参数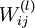 和
和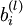 初始化为很小的接近于0的随机值(例如随机值由正态分布Normal(0,ε2)采样得到,把 ε 设为0.01), 然后运用批量梯度下降算法进行优化。由于 J(W,b) 是一个非凸函数,梯度下降很容易收敛到局部最优,但是在实践中,梯度下降往往可以取得不错的效果。最后,注意随机初始化参数的重要性,而不是全部初始化为0. 如果所有参数的初始值相等,那么所有的隐层节点会输出会全部相等,因为训练集是一样的,即输入一样,如果每个模型的参数还都一样,输出显然会相同,这样不论更新多少次参数,所有的参数还是会相等。随机初始化各个参数就是为了防止这种情况发生。
初始化为很小的接近于0的随机值(例如随机值由正态分布Normal(0,ε2)采样得到,把 ε 设为0.01), 然后运用批量梯度下降算法进行优化。由于 J(W,b) 是一个非凸函数,梯度下降很容易收敛到局部最优,但是在实践中,梯度下降往往可以取得不错的效果。最后,注意随机初始化参数的重要性,而不是全部初始化为0. 如果所有参数的初始值相等,那么所有的隐层节点会输出会全部相等,因为训练集是一样的,即输入一样,如果每个模型的参数还都一样,输出显然会相同,这样不论更新多少次参数,所有的参数还是会相等。随机初始化各个参数就是为了防止这种情况发生。
梯度下降每一次迭代用下面的方式更新参数W 和 b:
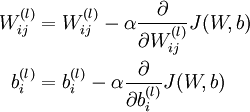
其中 α 是学习率。上述迭代的关键是计算偏导数。我们将给出一种方向传播算法,能够高效地计算这些偏导数。
由上面的总体的损失函数公式, 很容易得到偏导数公式如下:
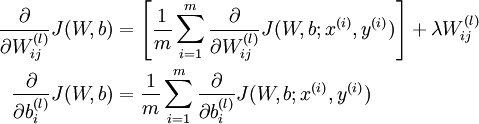
反向传播算法的思想是:给定某个训练样本(x,y),首先进行“前向传播”计算出整个网络中所有节点的激活值,包括输出节点的输出值。那么对于 l 层的节点 i ,计算它的“残差” 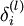 ,这个残差用来衡量该节点对输出的残差产生了多大程度的影响。对于输出节点,我们可以直接比较出网络的激活值与真正的目标值之间的残差,即
,这个残差用来衡量该节点对输出的残差产生了多大程度的影响。对于输出节点,我们可以直接比较出网络的激活值与真正的目标值之间的残差,即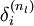 (nl 层就是输出层) 。对于隐层节点,我们用 l+1 层残差的加权平均值和 l 层的激活值来计算
(nl 层就是输出层) 。对于隐层节点,我们用 l+1 层残差的加权平均值和 l 层的激活值来计算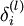 .
.
下面详细给出了反向传播算法的步骤:
1. 进行前馈传播,计算每一层的中所有节点的激活值
2. 对于输出层(第nl 层)的节点 i 的残差:
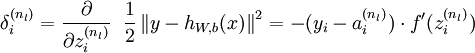
这里需要注意: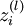 表示第 l 层节点 i 的所有输出之和,f 是激活函数,例如
表示第 l 层节点 i 的所有输出之和,f 是激活函数,例如![]() ,
,![]() 等,另外,最后一层(输出层)的假设函数
等,另外,最后一层(输出层)的假设函数 的输出值就是该层节点的激活值。
的输出值就是该层节点的激活值。
3. 对于 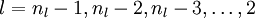
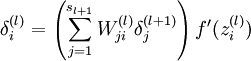
4. 计算偏导数:
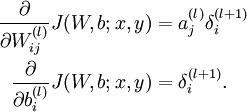
下面用矩阵-向量化的操作方式重写这个算法。其中" "表示matlab中的点乘。对于
"表示matlab中的点乘。对于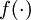 同样向量化,
同样向量化,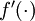 也作同样处理,即
也作同样处理,即![\textstyle f'([z_1, z_2, z_3]) =
[f'(z_1),
f'(z_2),
f'(z_3)]](http://deeplearning.stanford.edu/wiki/images/math/c/7/5/c7515c53b59e670ceee277e06c1229cb.png) .
.
BP算法重写如下:
1. 进行前馈传播,计算每一层的中所有节点的激活值
2. 对于输出层(第nl 层)的节点 i 的残差:
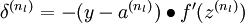
3. 对于 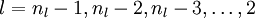
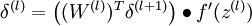
4. 计算偏导数:
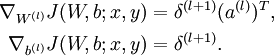
注意:在上面的第2步和第3步,,我们需要为每一个 节点 i 计算其 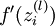 . 假设
. 假设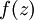 是sigmoid激活函数,在前向传播的过程中已经存储了所有节点的激活值
是sigmoid激活函数,在前向传播的过程中已经存储了所有节点的激活值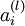 ,因此利用我们在
,因此利用我们在
稀疏自动编码之神经网络
中推导出的sigmoid激活函数的导数求法:对于sigmoid函数f(z) = 1 / (1 + exp( − z)),它的导函数为f'(z) = f(z)(1 − f(z)).可以提前算出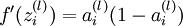 ,这里用到我们上面提到的
,这里用到我们上面提到的![]() .
.
最后,给出完整的梯度下降法.在下面的伪代码中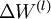 ,
,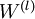 都是矩阵,
都是矩阵,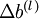 ,
,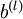 是向量。
是向量。
1. 对于每一层,即所有 l , 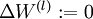 ,
, 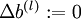 (设置为全零矩阵或者向量)
(设置为全零矩阵或者向量)
2. 从第一个训练样本开始,一直到最后一个(第 m 个训练样本):
a. 用反向传播计算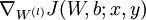 和
和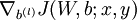
b. 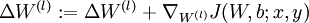 .
.
c. 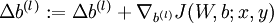 .
.
3. 更新参数:
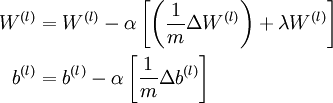
现在,我们可以重复梯度下降法的迭代步骤来减小损失函数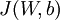 的值,进而训练出我们的神经网络。
的值,进而训练出我们的神经网络。
学习来源:http://deeplearning.stanford.edu/wiki/index.php/Backpropagation_Algorithm



