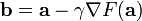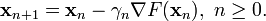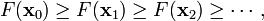【stanford】梯度、梯度下降，随机梯度下降

2012-12-13 22:35 Loull 阅读(6979) 评论(1) 编辑收藏举报

一、梯度gradient

http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6

在标量场f中的一点处存在一个矢量G，该矢量方向为f在该点处变化率最大的方向，其模也等于这个最大变化率的数值，则矢量G称为标量场f的梯度。

标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。

更严格的说，从欧氏空间Rⁿ到R的函数的梯度是在Rⁿ某一点最佳的线性近似。在这个意义上，梯度是雅戈比矩阵的一个特殊情况。

在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。

梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。

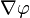一个标量函数 $\varphi$ 的梯度记为： $\nabla \varphi$ 或 $\rm grad \varphi$ ，其中 $\nabla$ （nabla）表示矢量微分算子。

二、梯度下降法

梯度下降法，基于这样的观察：

如果实值函数 $F(\mathbf{x})$ 在点 $\mathbf{a}$ 处可微且有定义，那么函数 $F(\mathbf{x})$ 在 $\mathbf{a}$ 点沿着梯度相反的方向 $-\nabla F(\mathbf{a})$ 下降最快。因而，如果

$\mathbf{b}=\mathbf{a}-\gamma\nabla F(\mathbf{a})$

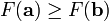对于 $\gamma>0$ 为一个够小数值时成立，那么 $F(\mathbf{a})\geq F(\mathbf{b})$ 。

$\mathbf{a}$ 是向量。

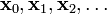考虑到这一点，我们可以从函数 $F$ 的局部极小值的初始估计 $\mathbf{x}_0$ 出发，并考虑如下序列 $\mathbf{x}_0, \mathbf{x}_1, \mathbf{x}_2, \dots$ 使得

$\mathbf{x}_{n+1}=\mathbf{x}_n-\gamma_n \nabla F(\mathbf{x}_n),\ n \ge 0.$

因此可得到

$F(\mathbf{x}_0)\ge F(\mathbf{x}_1)\ge F(\mathbf{x}_2)\ge \cdots,$

如果顺利的话序列 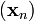$(\mathbf{x}_n)$ 收敛到期望的极值。注意每次迭代步长 $\gamma$ 可以改变。

梯度下降法的缺点是：

三、随机梯度下降法stochastic gradient descent，也叫增量梯度下降

由于梯度下降法收敛速度慢，而随机梯度下降法会快很多

–根据某个单独样例的误差增量计算权值更新，得到近似的梯度下降搜索（随机取一个样例）

–可以看作为每个单独的训练样例定义不同的误差函数

–在迭代所有训练样例时，这些权值更新的序列给出了对于原来误差函数的梯度下降的一个合理近似

–通过使下降速率的值足够小，可以使随机梯度下降以任意程度接近于真实梯度下降

•标准梯度下降和随机梯度下降之间的关键区别

–标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的

–在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算

–标准梯度下降，由于使用真正的梯度，标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长

–如果标准误差曲面有多个局部极小值，随机梯度下降有时可能避免陷入这些局部极小值中

刷新页面返回顶部

Loull