数字滤波器

　　滤波是信号处理中的一种基本而重要的技术，利用滤波技术可以在形形色色的信号中提取所需的信号，抑制不需要的干扰信号。按处理信号不同，滤波器可分为模拟滤波器与数字滤波器两大类。模拟滤波器是用来处理模拟信号或连续时间信号，数字滤波器是用来处理离散的数字信号。与模拟滤波器相比，数字滤波器具有诸多优点：可以用软件编程；稳定性高，可预测；不会因温度、湿度的影响产生误差，不需要高精度元件；很高的性能价格比。

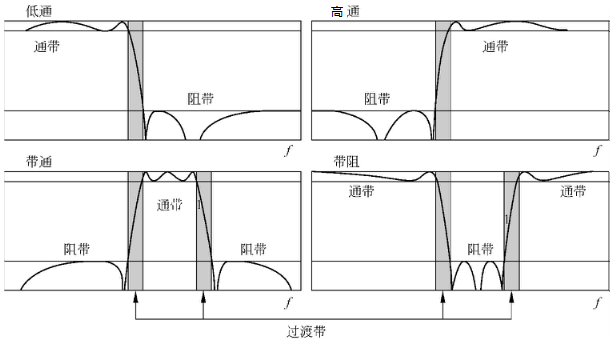
　　滤波器是频率选择电路，只允许输入信号中的一定频率成分通过，与模拟滤波器相同，按通带来划分可将数字滤波器分为4种类型：

（1）低通滤波器（Lowpass filter） ：通过低频，滤除高频。
（2）高通滤波器（Highpass filter）：通过高频，滤除低频。
（3）带通滤波器（Bandpass filter）：通过固定范围的频率。
（4）带阻滤波器（Bandstop filter）：滤除固定范围的频率。

以上 4 种滤波器的理想频率响应如下图所示。
　　滤波器允许通过的频率范围为通频带，理想滤波器通频带的增益为1，所以信号的幅值不变。截止频带是滤波器不允许通过的频率范围。理论上滤波器在通带应有单位增益(0 dB)，在阻带有0增益(-∞ dB)，然而在实际中通阻带之间有一个过渡范围，如下图所示。在这一范围，增益在0~1之间。在应用中，允许增益在单位增益上下轻微变化，即允许有通带纹波。这一点也是实际滤波器与理想滤波器的区别。阻带衰减在实际中不是无限的，通带纹波与阻带衰减可表示为：

 通带纹波= $20lg(\frac{A_o(f)}{A_i(f)})$ 

　　其中$A_0(f)$、$A_i(f)$分别是一定频率f下的输出和输入振幅，通带波纹的单位为分贝(dB)。

　　例如对于-0.02dB的波纹：$-0.02=20lg(\frac{A_o(f)}{A_i(f)}) \Rightarrow \frac{A_o(f)}{A_i(f)}=10^{-0.001}=0.9977$。这表明，输出和输入的幅值之比近似为1。当阻带有-60dB的衰减，则$\frac{A_o(f)}{A_i(f)}=10^{-3}=0.001$，表明输出的幅度是输入的1/1000。

• IIR和FIR滤波器

　　滤波器也可以按冲击响应来分类，对信号

$$x(i)=\begin{cases}1 & i=0 \\0 & i\neq 0\end{cases}$$

　　的响应为冲击响应，如下图所示。由傅里叶变换后的频率响应可知滤波器在不同频率下的增益。理想情况下，通带增益为1，阻带增益为0；所以频率在通带范围内的信号可完全通过，在阻带的信号则不能通过。

　　如果冲击响应经一段时间后增益为零，则滤波器为有限冲击响应滤波器(FIR)或递归数字滤波器，反之则为无限冲击响应滤波器(IIR)或非递归数字滤波器。其最基本的不同是FIR的输出只是由当前以及过去的输入值决定；而IIR的输出不但由当前以及过去的输入值决定，还与过去的输出值有关。

　　例如一个商店计算收款额，现在所卖商品的价格为$x(k)$，过去所卖商品的价格为$x(k-1)$，N为所有商品的总数，总额为$y(k)$，则：

$$y(k)=x(k)+x(k-1)+x(k-2)+...+x(1)$$

　　也可以写为

$$y(k)=y(k-1)+x(k)$$

　　上述两个公式对收款额的描述本质上是一样的，只是前一个公式只涉及到输入，而后一个公式不但有输入，而且还有输出。前一公式是非递归形式，即FIR；而后一个公式则是递归形式，即IIR。如果加上6%的税，则上式可以写为：$y(k)=1.06\{x(k)+x(k-1)+x(k-2)+...+x(1)\}$或$y(k)=y(k-1)+1.06x(k)$ 。前一个式子中有一个公因子1.06，而后一个式子中y(k-1)的因子是1，x(k)的因子是1.06。这些因子都是滤波器的系数因子。IIR滤波器中，与输入相乘的因子是前项因子，而与输出相乘的是递归因子。 

　　对IIR和FIR滤波器来说，前者有较平坦的幅频特性，而且由于它的递归性，可以减少存储需求；而后者可以实现相位不失真。由于前者的设计方法源于传统的模拟滤波器，且使用滤波器时人们主要关心幅频特性，所以IIR滤波器使用较多。数字信号处理中常见的IIR滤波器有：巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器、贝塞尔滤波器等，各个滤波器具有不同的频率特性。如果有各种不同的滤波器及参数，设计时就必须考虑选择最适合的滤波器。影响滤波器的因素有：是否需要线性相位；是否允许纹波；是否需要一个窄带的过渡带。在具体设计一种滤波器前，需对各种滤波器做多次试验。

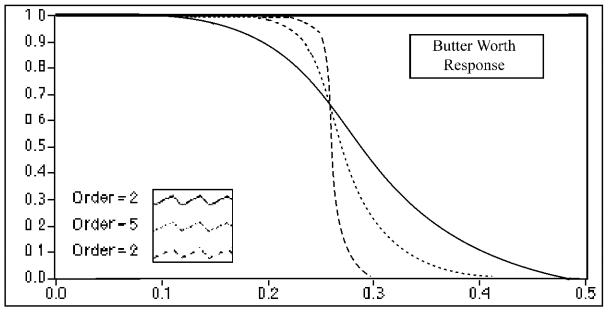
　　巴特沃斯滤波器的幅频特性表达式为：

$$|H(\omega )|=\frac{1}{\sqrt{1+\left(\frac{\omega }{\omega _c}\right){}^{2n}}}$$

　　式中$\omega_c$为通带截止频率（在截止频率处有3dB衰减），$n$为滤波器阶数（阶数越高，过渡带越窄）。从下图可以看出巴特沃斯滤波器在通带内具有最大平坦的幅频特性，在截止频率后单调下降。其频响特性是最平滑的，通带中是理想的单位响应，阻带中响应为零。  

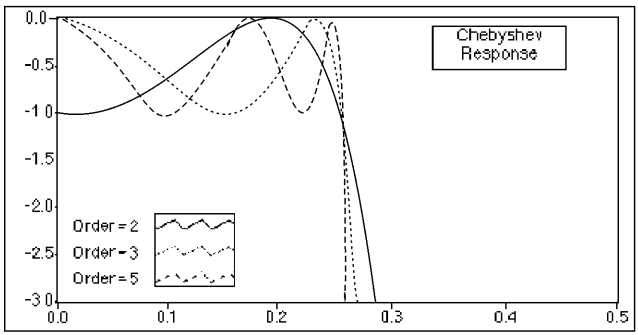
　　巴特沃斯滤波器在通带与阻带之间过度缓慢，相比于巴特沃斯滤波器，切比雪夫滤波器在通带与阻带之间能够达到快速的过渡。如下图所示，契比雪夫滤波器的频响特点是，在通带响应中有一个等幅的纹波，阻带中单位衰减。契比雪夫滤波器较巴特沃斯滤波器的优点是，用较少的阶数就能使过渡带很陡，从而加快了滤波速度，降低了绝对误差 。（分贝：表示功率量之比的一种单位，等于功率强度之比的常用对数的10倍；表示场量之比的一种单位，等于场强幅值之比的常用对数的20倍，即$1dB=10lgP=20lgV$。分贝刻度将宽的幅度范围压缩在一个较小的数集里，在声音、震动测量及显示频域信息时会经常用到。）

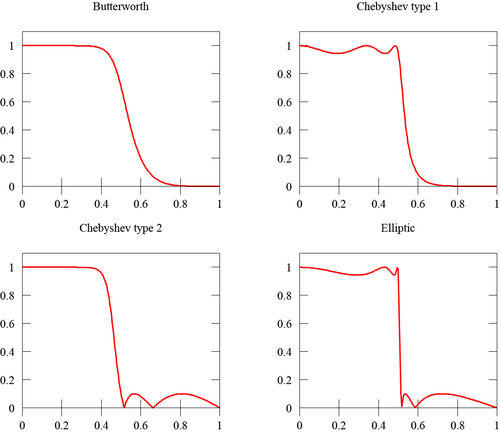
如下图所示，相同阶数时：
巴特沃斯滤波器通带最平坦，阻带下降慢；
切比雪夫滤波器通带等纹波，阻带下降较快；
椭圆滤波器在通带等纹波，阻带下降最快；
贝塞尔滤波器通带等纹波，阻带下降慢（即幅频特性最差，但是贝塞尔滤波器具有最佳的线性相位特性）

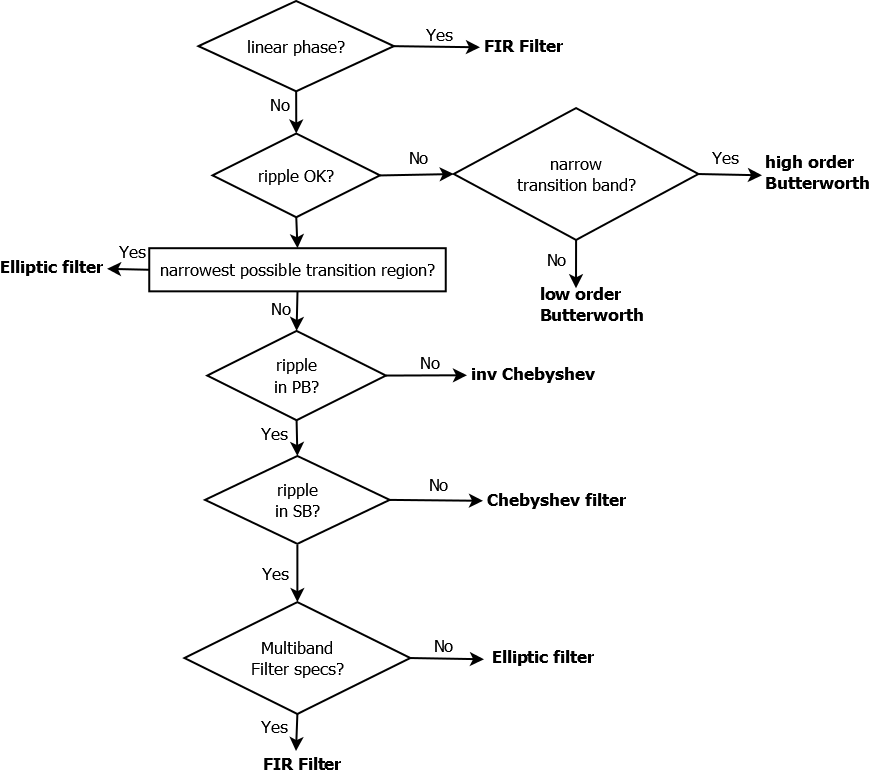
　　各个滤波器具有不同的频率特性，如果有各种不同的滤波器及参数，设计时就必须考虑选择最适合的滤波器。影响滤波器的因素有：是否需要线性相位；是否允许纹波；是否需要一个窄带的过渡带。下图表示如何选择滤波器。在具体设计一种滤波器前，需对各种滤波器做多次试验。 

• LabVIEW中的滤波器

　　在进行信号分析和处理时，分析数据的一般过程是：初始化缓冲区、数据分析、数据输出，再根据缓冲区中的数据块进行分析。这种基于数据块的分析方法难以实现高速实时分析。LabVIEW提供了一类逐点分析节点，可以一个数据点接一个数据点分析，此时数据分析是基于数据点的，可以实现实时处理。使用逐点分析可以与信号同步，数据丢失的可能性更小，对硬件设备采样率的要求更低。逐点分析节点位于函数选板的“信号处理→逐点”

　　关于使用逐点滤波器的范例见labview\examples\Signal Processing\Point by Point中的PtByPt and Array Based Filter VI

注意几点：

　　（1）采样频率

　　一般软件中数字滤波器模板中的频率都是归一的化频率，归一化的频率通过采样频率这一参数和实际频率对应起来。对于各种类型滤波，采样频率均应设置成滤波器输入信号的采样频率。

　　（2）纹波幅度

　　切比雪夫数字滤波器通带段幅频特性呈波纹状，需此参数控制纹波幅度，一般取0.1dB。巴特沃斯和贝塞尔滤波器通带段幅频特性曲线比较平坦，不需要此参数。

　　（3）截止频率

　　高截止频率f₂和低截止频率f₁（f_s为采样频率）必须符合条件：0 < f₁ < f₂ < 0.5f_s

　　(4) 滤波器阶数

　　随着阶数的提高，与理想滤波器的特性越接近。但由于它的延迟也和滤波阶数有关，所以滤波器的性能不能单纯的靠增加滤波器的阶数来提高，因为增加滤波器阶数的同时也会使延迟变大。实际测试中应充分了解测试信号和噪声的特点，然后选取合适的滤波方案。

　　另外也可以使用Express模块中的滤波器，Express VI将基本函数面向应用做了进一步的打包，为用户提供了更加方便、简洁的编程途径。使用 Express VI，初学者无需面对复杂的连线即可快速入门。对于一般用户，Express VI 也可以起到减少连线，简化框图，突出程序主脉络等作用 。