数论讨伐！线性筛！

【线性筛】

任务开始。

  • 什么是线性筛？线性就是O（n），筛就是往外剔。能不能想象出她的运作方式？
  • 此次任务的主要怪物：素数筛,欧拉筛和莫比乌斯筛

（1）线性筛素数

用于快速的求解一定范围以内的素数，首先我们要知道任何一个数n都可以拆成若干素数p的表述形式，即

n=P1a1+P2a2+P3a3+P4a4+P5a5+P6a6......

还有，如果一个数可以表示为i*prime[1]（一个数乘以另一个素数）那么它就不是素数（废话）

所以就有了线性筛这种东西

#include <cstdio>
#define N 10000050
/*
  线性筛 
  O(n)求n以内的素数 
*/
using namespace std;
int cnt,prime[N],n;
bool check[N];
int main()
{
    scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        if(!check[i])
            prime[++cnt]=i;
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>n)
                break;
            check[i*prime[j]]=1;
            if(i%prime[j]==0)
                break;
        }
    }
}

prime数组存的便是质数，准确的来说，是当前小于等于i的所有质数

而cnt就是当前的质数个数，这段代码无非就是把所有已知的素数与当前枚举的这个i的乘积标记为合数

但是这是怎么保证线性的呢？如果一个合数被多次筛掉，那么代价可要大得多

要让每个数只被筛掉一次，只有一种办法——让i*p中，p为i*p这个数最小的质数！（你没忘记怎么把数拆成质数吧？）

以下
  1. 为什么i*p中不用考虑p>i的情况？

若i是个质数，那么i*p就会被i*p与p*i筛掉两回，不行

若i是合数，那么i也可以被拆分

    （1）若i中最小的质数比p小，那么随之对应的就会有个更大的i来与其配合构成i*p，又会被筛两边，不行

    （2）若i中最小的质数等于或大于p，那i绝壁大于p啊喂！

        2.为什么i%prime[j]==0就break了？

如果发生了这种情况就意味着什么？——pj（prime[j]）是i的最小质因子！，同时i绝壁是个合数

也就是说i*px（x>j）这个新数最小的质因子往后都是pj，那么如果用px去筛i*px就会做二遍功

因此从这里往后都不用筛了，等着一个更大的i来筛就好了~！

感觉理解了吗？做做裸体题练练手（P1111 HSDFZOJ）

【回复药G】入手！

来，给你磕个药，咱们正式开筛！

（2）线性筛欧拉函数

欧啦欧啦欧啦欧啦欧拉欧拉欧拉

首先我们要知道什么是欧拉函数

对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）

这些请你先当作已知条件吧，我会开一个针对欧拉函数的讨伐任务

对，你就盯着第一条和φ(n*m)那条看就好了

对了还有第4条，它可以翻译成这样：

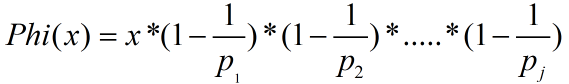其中p1到pj为x所有的质因子

如何求φ？

设p为素数

  1. Phi(p)=p-1(这个很好求对不)
  2. 给一个数x怎么求Phi(x*p)呢？

（1）若这个x满足x%p==0，那么这对于x*p意味着什么？从x变成x*p的过程中，质因子没有发生任何改变！

也就是说把式子中x换成x*p，剩下的关于质因子的部分一笔不动就行了，所以我们有了：Phi(x*p)=Phi(x)*p

（2）若x%p!=0。。。哎！好像x与p互质啊！所以Phi(x*p)=Phi(x)*Phi(p)=Phi(x)*(p-1)

给你呆码

#include <cstdio>
#define N 10000050
/*
  线性筛 
  O(n)求n以内的素数及欧拉函数值 
*/
using namespace std;
int cnt,prime[N],phi[N],n;
bool check[N];
phi[1]=1;
int main()
{
    scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        if(!check[i])
            prime[++cnt]=i,phi[i]=i-1;
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>n)
                break;
            check[i*prime[j]]=1;
            if(!i%prime[j])
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    return 0; 
}

 

顺带一提，因为使用了和素数筛相同的break机理，所以可以保证每个x*p只被最小的p筛一次，真是皆大欢喜~~

什么，你想要裸体题？这种东西都是作为预处理存在的ok？

（3）线性筛莫比乌斯函数

跟所谓的莫比乌斯环没有太大关系哦。。。

首先我们要知道什么是莫比乌斯函数

莫比乌斯函数是一个积性函数，符号记作μ，定义如下：

1）莫比乌斯函数μ(n)的定义域是N
2）μ(1)=1
3）当n存在平方因子时，μ(n)=0
4）当n是素数或奇数个不同素数之积时，μ(n)=-1
5）当n是偶数个不同素数之积时，μ(n)=1

 

 

虽然我们还不知道这个函数能做些什么，但有了这些定义后我们就应该有能力做出来

如何求μ？

设p为素数

  1. μ(p)=-1(这个很好求对不)
  2. 给一个数x怎么求μ(x*p)呢？

（1）若这个x满足x%p==0，那么这对于x*p意味着什么？从x变成x*p的过程中，多出了一个平方因子(p2)！

所以我们有了：μ(x*p)=0

（2）若x%p!=0。。。哎！从x变成x*p的过程中，多了一个新的质因子p，就是说质因子数量从奇变偶或者从偶变奇

又或者如果μ(x)=0，那么μ(x*p)仍然=0，所以就有了μ(x*p)=-μ(x)

拿着，呆码！

#include <cstdio>
#define N 10000050
/*
  线性筛 
  O(n)求n以内的素数及莫比乌斯函数值 
*/
using namespace std;
int cnt,prime[N],Mob[N],n;
bool check[N];
int main()
{
    Mob[1]=1;
    scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        if(!check[i])
            prime[++cnt]=i,Mob[i]=i-1;
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>n)
                break;
            check[i*prime[j]]=1;
            if(!i%prime[j])
            {
                Mob[i*prime[j]]=0;
                break;
            }
            else
                Mob[i*prime[j]]=-Mob[i];
        }
    }
    return 0; 
}

 

没错，这个break还是你熟悉的break。。。

什么，你想要裸体题？这种东西找到了一定要分享给我啊233

（4）结语

其实这后两种筛法都是由线性筛进化而来的，你可以很明显的看出她们的共同点

什么，你没看出来？给你看看我找的这个图：

没错，就这么煎蛋~

小伙伴们问在不熟练的情况下怎么记住模板，其实三种筛法模板是一样的，

所以只需要记住素数模板和欧拉和莫比乌斯函数部分的分类讨论就是了。

这三种筛法学会了之后，今后无论是什么筛我相信你一定能得心应手啦！赶快趁热噶素材做装备啊！

数论区域可不止这几只小怪！今后你托付性命的武器还得你自己打造！学会了这样重要的基础算法后，

便可以便可信心十足地奔赴曾经认为高深莫测的版块——数论了。祝你狩猎愉快！

 

获得部位破坏奖励：素材【if(i%prime[j]==0)break;】入手！

end————————2018/3/2

 

posted @ 2018-03-01 16:17  瞬闪影  阅读(293)  评论(0)  编辑  收藏  举报