2017-2018-1 20155226《信息安全系统设计基础》第2周学习总结

2017-2018-1 20155226《信息安全系统设计基础》第2周学习总结

教材学习内容总结

第二章 信息的表示和处理

  • 计算机存储和处理信息以二值信号表示。
  • 三种最重要的数字表示法
  1. 无符号：基于传统的二进制表示法，大于等于0
  2. 补码：有符号整数
  3. 浮点数：实数的科学计数法的以二进制为基数的版本
  • 缓冲区溢出漏洞：计算机的表示法是用有限数量的位来对应一个数字编码，当结果太大不能表示时就会发生溢出。人为的溢出是有一定企图的，攻击者写一个超过缓冲区长度的字符串，植入到缓冲区这时可能会出现两种结果：一是过长的字符串覆盖了相邻的存储单元，引起程序运行失败，严重的可导致系统崩溃；另一个结果就是利用这种漏洞可以执行任意指令，甚至可以取得系统root特级权限。

2.1信息存储

字长

机器级程序将存储器视为一个非常大的字节数组，称为虚拟存储器。存储器的每个字节都能由唯一的数字来标识，称为地址。字长用来指明整数和指针数据的标称大小，虚拟地址空间的大小由字长决定，对于一个字长为w位的机器而言，虚拟地址的范围为0-2^w-1。

数据大小
  • 程序可移植性的要求是使程序对不同数据类型的确切大小不敏感
  • gcc -m32 可以在64位机上生成32位的代码
寻址和字节顺序
  • 对于跨越多字节的程序对象，必须建立两个规则：
  1. 对象的地址是什么
  2. 在存储器中这些字节如何排列
  • 多字节对象被存储为连续的字节序列，对象的地址为所使用字节中最小的地址
  • 大端法&小端法：最低有效字节在最前面的方式称为小端法，最高有效字节在最前面的方式称为大端法。字节顺序是网络编程的基础，小端是“高对高、低对低”，大端与之相反。
  • 字节顺序可见的三种情况：
  1. 网络应用程序代码编写时必须遵循已建立的关于字节顺序的规则
  2. 反汇编器显示（确定可执行文件所表示的指令序列的工具）
  3. 编写规避正常的类型系统的程序时，可以使用强制类型转换来允许一种数据类型引用一个对象
  • 使用sizeof来确定对象使用的字节数，sizeof（T）返回存储一个类型为T的对象所需字节数。
布尔代数
  • 布尔代数起源于数学领域，是一个用于集合运算和逻辑运算的公式：〈B，∨，∧，¬ 〉。其中B为一个非空集合，∨，∧为定义在B上的两个二元运算，¬为定义在B上的一个一元运算。
  • 通过布尔代数进行集合运算可以获取到不同集合之间的交集、并集或补集，进行逻辑运算可以对不同集合进行与、或、非。
  • 所有逻辑运算都可以用与、或、非表达（最大式、最小式），而与或非可以用“与非”或“或非”表达，所以，只要一个与非门，就可以完成所有的逻辑运算。
  • 位向量：表示有限集合，在实际应用中位向量用来对应集合编码。
  • C语言的特性：支持按位布尔运算，确定一个位级表达式的结果的最好方法就是将十六进制转化为二进制进行运算后再转回十六进制。
C语言中的逻辑运算
  • || OR
  • && AND
  • ！ NOT
  • 只要一个与非门，就可以完成所有的逻辑运算。
  • 逻辑运算认为，所有非零参数都为TRUE，参数0为FALSE，返回值分别为1和0。
  • 逻辑运算符和对应的位运算之间的重要区别是，如果对第一个参数求值就能确定表达式的结果，那么就不会对第二个参数求值，避免运算。
C语言中的移位运算

对于一个位表示为[xn-1，xn-2，…，x0]的操作数x，C表达式x<>k，但是它的行为有点微妙。一般而言，机器支持两种形式的右移：逻辑右移和算术右移。逻辑右移在左端补k个0，得到的结果是[0，…，0，xn-1，xn-2，…，xk]。算术右移是在左端补k个最高有效位的值，得到的结果是[xn-1，…，xn-1，xn-1，xn-2，…，xk]。

2.2整数表示

整形数据类型
  • C语言支持多种整形数据类型——表示有限范围的整数。
  • 要用C99中的“long long”类型，编译是要用 gcc -std=c99
无符号数的编码

  • 假设一个整数数据类型有w位。我们可以将位向量写成x→，表示整个向量，或者写成[xw-1 ，xw-2，…，x0]，表示向量中的每一位。把x→看做一个二进制表示的数，就获得了x→的无符号表示。

  • 无符号二进制有一个很重要的属性，就是每个介于0~2^w-1之间的整数都有唯一一个w为的值编码，函数为一个双射。

补码编码

  • 最常见的有符号数的计算机表示方式就是补码形式。在这个定义中，将字的最高有效位解释为负权。所能表示的数值范围[-2(w-1)~2(w-1)-1]，在可表示的范围内每个数字 都有一个唯一的w位的补码编码，函数为一个双射。

       注意

  • 补码的利用寄存器的长度是固定的特性简化数学运算。想想钟表，12-1 等价于 12 + 11，利用补码可以把数学运算统一成加法，只要一个加法器就可以实现所有的数学运算。

  • 补码的范围是不对称的：|TMin| = |TMax| + 1，也就是说，TMin没有与之对应的正数。这导致补码运算的某些特殊的属性，并且容易造成程序中细微的错误。之所以会有这样的不对称性，是因为一半的位模式（符号位设置为1的数）表示负数，而一半的数（符号位设置为0的数）表示非负数。因为0是非负数，也就意味着能表示的正数比负数少一个。

  • 最大的无符号数值刚好比补码的最大值的两倍大一点：UMaxw = 2 TMaxw + 1。补码表示中所有表示负数的位模式在无符号表示中都变成了正数。

符号数的其他表示方法
  • 反码：除了最高有效位的权是-(2w-1-1)而不是-2w-1，它和补码是一样的
  • 原码：最高有效位是符号位用来确定剩下的位应该取负权还是正权。

2.3整数运算

无符号加法
  • 考虑两个非负整数x和y，满足0≤x， y≤2w-1。每个数都能表示为w位无符号数字。然而，如果计算它们的和，我们就有一个可能的范围0≤x + y≤2w+1-2。表示这个和可能需要w + 1位。这种持续的“字长膨胀”意味着，要想完整地表示算术运算的结果，要对字长做限制。
  • 无符号运算可以被视为一种模运算形式。无符号加法等价于计算和模上2w。可以通过简单的丢弃x + y的w + 1位表示的最高位，来计算这个数值。
  • 溢出：一个算术运算溢出，是指完整的整数结果不能放到数据类型的总长限制中去。
补码的非
  • 范围在-2w-1≤x < 2w-1中的每个数字x都有+wt下的加法逆元。
    对于范围在[-2(w-1),2(w-1))中的x，补码的非运算有如下两种情况：x=-2^(w-1)时，为-2^(w-1), x>-2^(w-1)时，为-x
无符号乘法
  • 范围在0≤x, y≤ 2w-1内的整数x和y可以表示为w位的无符号数，但是它们的乘积x · y的取值范围为0到(2w-1)2 = 22w-2w+1+1之间。这可能需要2w位来表示。不过，C语言中的无符号乘法被定义为产生w位的值，就是2w位的整数乘积的低w位表示的值。可以看作等价于计算乘积模2w。
    因此，w位无符号乘法运算* wu的结果为：
补码乘法
  • c语言中的有符号乘法是通过将2w位的乘积截断为w位的方式实现的。也就是说，需要mod 2的w次幂。所以，对于无符号和补码乘法来说，乘法运算的位级表示都是一样的。
乘以常数
  • 编译器使用了一项重要的优化，试着用移位和加法运算的组合来代替乘以常数因子的乘法。将整数拆成2的幂相加，再利用移位进行计算(左移)，最后将结果相加。同理，对于非负数来说，算术右移k位与除以2^k是一样的。

2.4浮点数

浮点表示对形如V = x×2y的有理数进行编码。它对执行涉及非常大的数字（|V |>>0）、非常接近于0（|V |<<1）的数字，以及更普遍地作为实数运算的近似值的计算，是很有用的。

教材学习中的问题和解决过程

  1. 补码加法

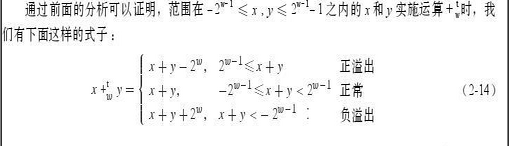
代码托管

其他（感悟、思考等，可选）

本章内容有点难理解，特别是和代码联系起来后，本身我就对数字不敏感，所以需要下更多功夫。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 25/50 1/1 10/10
第二周 82/132 1/3 35/50

尝试一下记录「计划学习时间」和「实际学习时间」，到期末看看能不能改进自己的计划能力。这个工作学习中很重要，也很有用。
耗时估计的公式
：Y=X+X/N ，Y=X-X/N，训练次数多了，X、Y就接近了。

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

  • 计划学习时间:20小时

  • 实际学习时间:35小时

  • 改进情况：这是国庆后总学习时间

(有空多看看现代软件工程 课件
软件工程师能力自我评价表)

参考资料

posted @ 2017-10-15 11:24  20155226田皓宇  阅读(163)  评论(0)  编辑  收藏  举报