20145221 《信息安全系统设计基础》第3周学习总结

20145221 《信息安全系统设计基础》第3周学习总结

教材学习内容总结

信息的表示和处理

三种数字表示

  • 无符号数：基于传统的二进制表示法，表示大于或等于零的数字
  • 补码：表示有符号数，可为正可为负的数字
  • 浮点数：表示实数的科学计数法的以二为基数的版本
  • 整数运算和浮点数运算有不同的数学属性，因为它们处理数字表示有限性的方式不同，整数的表示虽然只能编码一个相对较小的数值范围，但这种表示精确；浮点数编码数值范围相对较大，但是近似的。

信息存储

  • 字节：

    • 计算机最小的可寻址的存储器单位——字节
    • 一个字节的值域：00H-FFH

  • 字：

    • 每个计算机都有一个字长，指明整数和指针数据的标称大小。因为虚拟地址是以这样的一个字来编码的，所以字长最重要的系统参数就是虚拟地址空间的最大大小。
    • 对于一个字长为w位的机器而言，虚拟地址的范围为0~2^w-1,程序最多访问2^w字节。
    • w=32或64：也就是我们通常所说的电脑是32位还是64位。也可以理解为CPU一次处理数据的位数。

  • 数据大小：

    • C99特性：当没有-m32或-m64参数时，一般情况下会生成跟操作系统位数一致的代码；gcc -m32 XXX.c可以在64位机上（比如实验楼的环境）生成32位的代码。

  • 寻址和字节顺序：

    • 小端法：最低有效字节在前面——“高对高，低对低”。
    • 大端法：最高有效字节在前面。
    • 理解：我们一般用到的是小端法，比如在X86汇编中我们接触到的就是小端法。小端法的特点是“高对高，低对低”，但是其每个字节的内部是不变化顺序的，这个不需要死记，想想汇编上课时学的内存示意图，CPU以每个字节为单位寻址，所以字节内部的顺序是不变化的。
    • 例子：0x1234567，小端法67 45 23 01，大端法：01 23 45 67

  • 强制类型转换

  • 表示字符串和表示代码

    • 字符串：c语言中字符串被编码成为一个以null（值为0）字符结尾的字符数组。多使用ASCII字符码。在使用ASCII字符码的任何系统上都能得到相同的结果，与字节顺序和字大小规则无关，所以文本数据比二进制数据具有更强的平台独立性。
    • 代码：二进制代码在不同的操作系统上有不同的编码规则，所以二进制代码是不兼容的。例如：char *使用机器的全字长，在32位中占4个字节，而在64位的机器中则占8个字节。

布尔代数

  • 运算符号：
    • 与：&&（位与：&）
    • 或：||（位或：|）
    • 非：!(位非：~)
    • 位异或：^
  • 位向量：有固定长度为w、由0和1组成的串。
    • 位向量的应用——表示有限集合。
  • 掩码运算：掩码是位运算的重要应用，这里掩码是一个特定位模式，表示从一个字中选择一个位的集合。对特定位可以置一，可以清零。
    • 例子：任取一个数x=0x123ABCDE，x&0xFF = 0x000000DE
    • 有点类似计算机网络中“子网掩码”这个概念，可以对照理解。

整数表示

  • 整型数据类型
    • 表示有限范围的整数，每种类型都能用关键字来指定大小，还可以指定是非负数（unsigned）还是负数（默认）。这些不同大小的分配的字数会根据机器的字长和编译器有所不同。
  • 取值范围
    • 32位机器和64位机器对于同一数据类型的典型取值范围是有所不同的。
    • 典型取值范围中，取值范围不对称——负数的范围比整数的范围大1。
    • c语言标准定义的每种数据类型必须能够表示的最小的取值范围中，正数和负数的取值范围是对称的。
    • 要用C99标准中的“long long”类型，编译是要用gcc -std = c99
  • 无符号数的编码
    • 编码方法详见课本P39，之前学过，不作赘述。
    • 对于长度为w的位向量，都有一个唯一的值与之对应；反过来，在0~2^w-1之间的每一个整数都有一个唯一的长度为w的位向量二进制表示与之对应。二者之间存在一个双射的关系。
  • 补码编码——有符号数的编码
    • 我们都知道补码的最高位是表示符号位，解释为负权，“权重”为-2的（w-1）次方，即无符号表示中的权重的负数。符号位为1，表示值为负，符号位为0，表示值为非负（不是正，因为有0）
    • 补码的映射关系同样是一一对应的
    • 补码的范围：-2^(w-1)~2^(w-1)-1，即|TMin|=|TMax|+1——因为非负数中0的存在。
    • 无符号数编码（U）和补码（T）：UMax = 2 TMax + 1
    • 大多数情况下用补码来表示有符号数，并且具有的是典型的取值范围。
    • 有符号数的其他表示方法：
      • 原码
      • 反码
      • 相关介绍不在此赘述
  • 有符号数和无符号数的转换
    • 处理同样字长的有符号数和无符号数之间相互转换的一般规则：数值可能会改变，但是位模式不变。
    • c语言允许无符号数和有符号数之间的转换，转换的原则是底层的位表示不变。
    • 当从无符号数转换为有符号数是，效果是应用函数U2T，从有符号数转化为无符号数时，应用函数T2U，其中w表示数据类型的位数。
  • 扩展
    • 从一个较小的数据类型转换为较大的数据类型，同时保持数值不变。
    • 零扩展：多用于无符号数转换为一个更大的数据类型。只需在开头加上0即可。
    • 符号扩展：多用于补码数字转换，最高有效位是什么，就添加什么。
    • 注：无符号和有符号数字之间的转换，和数据的大小的转换，这之间的相对顺序能够影响到一个程序的行为。
  • 截断数字
    • 不用额外的位来扩展数值，而是减少表示一个数字的位数。而这么做可能会改变它的值，这也是溢出的一种形式。
    • 将一个w位的数截断为k位数字时，就会丢弃高w-k位。
    • 对于无符号数来说，就相当于 mod 2的k次幂
    • 对于有符号数来说，先按照无符号数截断，然后再转化为有符号数
    • 具体的公式参见书P52页。
  • 无符号数适用范围
    • 适用于没有任何数字意义的位的集合，比如地址；
    • 又或者实现模运算、多精度运算的时候，数字由字的数组表示的时候。
  • 有符号数适用范围
    • 编程中多用有符号数

整数运算

  • 无符号运算
    • 无符号运算本质上就是模运算，mod 2的w次幂。
    • 加法
      • 涉及到的相关知识有：交换群（阿贝尔群），单位元，加法逆元等等。计算起来很简单。
    • 乘法
      • 两个w位的无符号数相乘，实际上是截取了低w位，但是等价于mod 2的w次幂。
      • 总之就是模幂运算。
  • 补码运算
    • 加法运算：两个数的w位补码之和与无符号之和有完全相同的位级表示。
    • 溢出：
      • 补码加法的溢出情况比无符号运算更为复杂，分为正溢出、正常、负溢出。正溢出就是超过正数的最大范围，负溢出就是超过负数的最大范围，具体的公式在书58页，正负溢出的范围和原因，直观一点的图在59页。
      • 但是其实公式里给的本质仍然是模运算，模掉w位的补码最高有效位的权重2的w次幂。
    • 非运算：
      • 对于范围在[-2^(w-1),2^(w-1))中的x，补码的非运算有如下两种情况：
      • x=-2(w-1)时，为-2(w-1)
      • x>-2^(w-1)时，为-x
    • 乘法运算：同无符号乘法。若为截断后的结果，则取结果的后w位作为计算结果。无符号运算和补码运算在“+”、“-”、“*”在位级上有相同的结果。
    • 乘以常数：对于某个常数K的表达式x*K生成代码，编译器会将K的二进制表示表达为一组0或1的交替的序列： [(0…0)(1…1)(0…0)…(1…1)]，可以用以下两种形式来计算这些乘积的结果：
      • A：(x<<n)+(x<<n-1)+……+(x<<m)
      • B：(x<<n+1)-(x<<m)
    • 除以2的幂：设x/K,令K=2^n,
      • 当x为正数时，计算 x>>n;
      • 当x为负数时，将x加上偏置量，即加上2^n-1(即K-1),计算** (x+偏置量)>>n**。

浮点数

  • 浮点表示对形如V=x X (2^y)的有理数进行编码，适用于：
    • 非常大的数字
    • 非常接近于0的数字
    • 作为实数运算的近似值
    • IEEE浮点标准：IEEE标准754
  • 二进制小数：
    • 二进制点左边第i位，权为2i；右边第i位，权为(1/2)i。
    • 增加二进制表示的长度可以提高表示的精度。
  • IEEE浮点格式：
    • 表示形式：V=(-1)^s * M * 2^E
    • 符号：s决定这个数是正还是负。0的符号位特殊情况处理。
    • 尾数：M是一个二进制小数，范围为1~2-ε或者0~1-ε，ε=(1/2)^n。
    • 阶码：E对浮点数加权，权重是2的E次幂（可能为负数）。
  • 根据阶码的值，被编码的值可分为三种：
    • 情况一：规格化的值（当阶码字段不全为0或全为1时），阶码 E = e-Bias（e为无符号整数）；
    • 偏置值Bias = 2^(k-1)-1；尾数 M = 1+f（小数字段frac的解释为描述小数值f，二进制小数点在小数字段最高有效位的左边）。
    • 情况二：非规格化的值 （当阶码字段全为0时），E = 1-Bias；Bias = 2^(k-1)-1；M = f。
    • 情况三：特殊值 （当阶码字段全为1时），当小数域全为0时， 当s=1时，为-∞；当s=0时，为+∞；当小数域不全为0时，为NaN。
  • 浮点数的舍入：IEEE浮点格式定义了四种不同的舍入方法：
    • 向偶舍入(默认)：将数字向上或向下舍入，是的结果的最低有效数字为偶数。能用于二进制小数。
    • 向零舍入：把整数向下舍入，负数向上舍入。
    • 向下舍入：正数和负数都向下舍入。
    • 向上舍入：正数和负数都向上舍入。
  • 浮点运算：
    • 浮点加法：不满足结合性、满足单调性。
    • 浮点乘法：不满足结合性、满足单调性，在加法上不满足分配性。

教材学习中的问题和解决过程

教材P24中Perl脚本

  • 书中给了一个Perl脚本，当初并不知道怎么运行，按照书上给的指令试了试发现行不通

  • 最后转念一想，既然是Perl脚本，那自然应该有Perl脚本的相关语句，不管怎样，先在终端窗口中输入perl看看ubuntu中是否自带编译工具，输入完毕之后发现并没有提示异常，说明系统中有这个指令，尝试着在指令前加入perl，发现可行

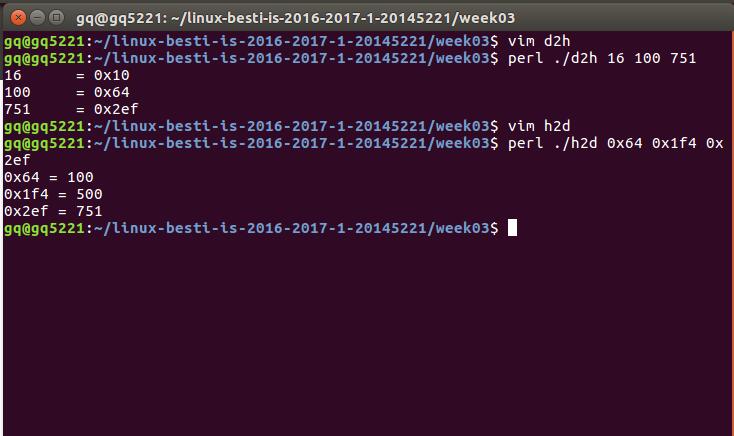
  • 另外，可以用man perl指令调用帮助文档进行查看（我装了中译版，所以显示中文）

本周代码托管截图

  • 托管如下：

其他（感悟、思考等，可选）

  • 这周主要学习了信息的表示和处理，其实有很多知识我们在之前的课程中都已接触过：《计算机导论》、《HDL数字逻辑电路》、《C语言程序设计》、《Java程序设计》、《汇编语言程序设计》。只不过不是很系统，也不是很深刻，只知道是什么不知道为什么。通过这一章节的学习，从操作系统出发，了解了内存中的存储读取机制，以及各种标准对信息的表示与要求，更深层次的了解到了信息在计算机中的表示。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 200/200 2/2 20/20 学习了Linux常用命令
第二周 79/279 1/3 30/50 了解vim,gcc,gdb基本操作
第三周 182/461 1/4 25/75 更深层次了解信息处理

参考资料

posted @ 2016-10-02 23:17  20145221高其  阅读(281)  评论(0)  编辑  收藏  举报