20145219 《信息安全系统设计基础》第03周学习总结
20145219 《信息安全系统设计基础》第03周学习总结
教材学习内容总结
信息的表示和处理
-
gcc 编译
使用C99特性时
gcc -std=c99 xxx.c实验楼环境为64位,编译为32位机器码:gcc -m32 xxx.c
第二章 信息的表示与存储
-
信息存储
1、三种数字:无符号数、有符号数(2进制补码)、浮点数
无符号:基于传统二进制表示法,表示大于或者等于零的数字。 补码:表示有符号整数的最常见方式。 浮点数:表示实数的科学计数法的以二为基数的版本。2、进制转换:二进制、八进制、十进制、十六进制(转换:以二进制作为中间变量)。
十六进制:以0x或0X开头表示,字符A-F可大写、可小写、也可混用。
3、
gcc -m32:可以在64位机上(比如实验楼的环境)生成32位的代码。当没有
-m32或-m64参数时,一般情况下会生成跟操作系统位数一致的代码4、字节顺序:字节顺序是网络编程的基础,是指占内存多于一个字节类型的数据在内存中的存放顺序,通常有小端、大端两种字节顺序。
小端法:指低字节数据存放在内存低地址处,高字节数据存放在内存高地址处。 大端法:是高字节数据存放在低地址处,低字节数据存放在高地址处。5、逻辑运算(结果是1或0)
所有逻辑运算都可以用与、或、非表达(最大式、最小式),而与或非可以用“与非”或“或非”表达,所以,只要一个与非门,就可以完成所有的逻辑运算。
逻辑与(&&):遇0为0; 逻辑或(||):遇1为1; 逻辑非 (!):遇0为1,遇1为0;6、位运算(结果是位向量)
按位与(&):二进制每一位遇0为0; 按位或(|):二进制每一位遇1为1; 按位异或(^):0^0=0,0^1=1,1^0=1,1^1=0; 按位取反(~):二进制每一位取反。7、掩码:位运算的重要应用,表示从一个字中选择一个位的集合。对特定位可以置一,可以清零。
-
整数表示
1、整型数据类型
char:字符型数据,占用一个字节 unsigned char:无符号字符型数据,占用一个字节 short:短整形数据,占用两个字节 unsigned short:无符号短整型数据,占用两个字节 int:整形数据,占用两个字节 unsigned int:无符号整型数据,占用两个字节 long:长整型数据,占用四个字节 unsigned long:无符号长整型数据,占用四个字节要用C99中的“long long”类型,编译是要用
gcc -std=c99。2、补码
二进制补码形式的三个特点:
(1)二进制补码的范围是不对称的:|TMin|=|TMax|+1,即不存在与最小值相对应的整数,这容易造成程序中细微的错误。 (2)位数相同的前提下,无符号数的最大值刚好是二进制补码最大值的2倍加1:UMax=2TMax+1。 (3)二进制补码中的-1与UMax有相同的位表示——全1位串。补码的利用寄存器的长度是固定的特性简化数学运算,利用补码可以把数学运算统一成加法,只要一个加法器就可以实现所有的数学运算。
3、有符号数和无符号数的转换(T2U表示补码到无符号数的转换,U2T表示无符号数到补码的转换,w表示数据类型的位数)
(1)有符号数转换为无符号数时,负数转换为大的正数(可以理解为原值加上2的n次方),而正数保持不变。
x<0 T2Uw(x)=x+2^w x>0 T2Uw(x)=x+2^w(2)无符号数转换为有符号数时,对于小的数将保持原值,对于大的数则转换为负数(可以理解为原值减去2的n次方)
u<2^(w-1) U2Tw(u)=u u>=2^(w-1) U2Tw(u)=u-2^w在无符号整数和有符号整数之间进行强制类型转换时,并未改变对象的位模式,改变的是位模式的解释方式。处理同样字长的有符号数和无符号数之间相互转换的一般规则是:数值可能会改变,位模式不变。
4、0扩展和符号扩展
0扩展:要将一个无符号数转换为一个更大的数据类型,只需简单的最高位前加0。 符号扩展:将一个补码数字转换为一个更大的数据类型,在表示中添加最高有效位值的副本。 -
整数运算
1、算术运算溢出:完整的整数结果无法放到数据类型的字长限制中。
执行C程序时,不会将溢出作为错误而发出警告信号。
判断无符号运算是否溢出,例如s=x+y(s、x、y均为无符号数),唯一可靠的判断标准就是s<x或s<y。
2、关于整数运算的最后思考
计算机执行的“整数运算”实际上是一种模运算。
表示数字的有限字长限制了可能的值的取值范围,结果运算可能溢出。
补码表示提供了一种既能表示负数也能表示正数的灵活方法,同时使用了与执行无符号算术相同的位级实现,无论运算数是以无符号形式还是补码形式表示,都有完全一样或者非常类似的位级行为。
-
浮点数
1、浮点数IEEE标准
(1)用
V = (-1)s * M * 2E的形式来表示一个数:符号:s决定这个数是负数(s = 1)还是正数(s = 0),而对于数值0的符号位解释作为特殊情况处理。 尾数:M是一个二进制小数,它的范围是1 ~ 2-ε,或者是0 ~ 1-ε。 阶码:E的作用是对浮点数据加权,这个权重是2的E次幂(可能是负数)。(2)浮点数的位表示划分为三个字段,分别对这些值进行编码:
一个单独的符号位 s 直接编码符号 s。 k位的阶码字段 exp = e(k-1)……e1e0编码阶码 E。 n位小数字段 frac = f(n-1)……f1f0编码尾数 M,但是编码出来的值也依赖于阶码字段的值是否等于0。2、浮点数运算的不精确性与舍入:因为表示方法限制了浮点数的范围和精度,浮点运算只能近似的表示实数运算。
IEEE浮点格式定义了四种不同的舍入方法:
向偶舍入(默认):将数字向上或向下舍入,是的结果的最低有效数字为偶数。能用于二进制小数。 向零舍入:把整数向下舍入,负数向上舍入。 向下舍入:正数和负数都向下舍入。 向上舍入:正数和负数都向上舍入。3、float/double类型
C提供两种浮点类型:float和double,在支持IEEE浮点标准的机器上分别表示单精度和双精度浮点数。
float中:s、exp和frac字段分别为1位、k = 8 位和n = 23位,得到一个32位的表示; double中:s、exp和frac字段分别为1位、k = 11 位和n = 52位,得到一个64位的表示。4、整数与浮点数转换规则
从int转换成float:数字不会溢出,但有可能舍入 从int或float转换成double:能够保留精确的数值 从double转换成float:可能溢出为正负无穷,由于精确度变小也有可能被舍入 从float或double转换成int:值将会向零舍入,进一步来说值可能溢出
代码调试
- p28: 代码执行一下


- p52: 深入思考一下代码和结果
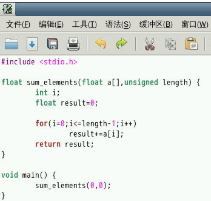

这个错误就是因为有符号数到无符号书的隐式转换导致的,这种强制转换是在代码没明确指示下发生的
本周代码托管截图



其他(感悟、思考等,可选)
本周的知识是信息的相关基本知识,涉及到信息的存储方式、有符号数和无符号数的表示、补码相关运算、浮点数和整数的关系等,学好这些知识能够有效地帮助我们编写出正确且高效的代码。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第零周 | 0/0 | 1/1 | 15/15 | |
| 第一周 | 0/0 | 1/2 | 25/40 | |
| 第二周 | 62/62 | 1/3 | 25/65 | |
| 第三周 | 176/238 | 1/4 | 20/85 |





