20135327郭皓——信息安全系统设计基础第三周学习总结
第2章 信息的表示和处理
三种重要的数字表现形式:
1、 无符号数:编码基于传统的二进制表示法,表示大于或等于零的数字。
2、 补码:编码是表示有符号整数的最常见方法,有符号整数就是可以为正或者是负的数字。
3、 浮点数:编码是表示实数的科学计数法的以二位基数的版本
2.1 信息储存
大多数计算机使用8位块,或者字节,作为最小的可寻址的储存器单位,而不是在储存器中访问单独的位。
虚拟储存器:机器级程序将储存器视为一个非常大的字节数组。
地址:储存器的每个字节的唯一的数字标识。
虚拟地址空间:所有可能地址的集合
十六进制表示法:0x开头,10~15对应A~F
十进制十六进制转换:辗转相除法
字: 字长:指明整数和指针数据的标称大小。字长决定最重要的系统参数就是虚拟地址空间的最大大小。
数据大小:计算器和编译器支持不同方式编码的数字格式,也具有处理单个字节的指令或2字节,4字节,8字节整数的指令。
寻址和字节顺序:最高有效位前八位和最低有效位后八位。是网络编程基础
小端法:某些机器选择在存储器中按最低有效字节到最高有效字节
大端法:某些机器选择在存储器中按最高有效字节到最低有效字节
注意:小端法“高对高,低对低”大端与之相反。
表示字符串:文本数据比二进制数据具有更强的独立性
布尔代数:二进制是计算机编码存储和操作信息的核心
C语言中的位级运算:C语言支持按位的布尔运算。与或非,异或同或常见用法就是实现掩码运算。
C语言中的逻辑运算:逻辑运算符&& 和 || 与它们对应的位级运算& 和 | 之间第二个重要的区别是,如果对第一个
C语言中的移位运算:C 语言标准并没有明确定义应该使用哪种类型的右移。对于无符号数据,右移必须是逻辑的
2.2整数表示
1.整型数据类型
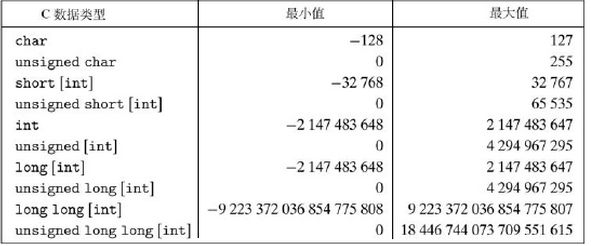
C 和C++默认支持有符号数和无符号数,Java只支持有符号数。
2.无符号数的编码
3.补码编码:最高位有效位也称符号位,权重为-2^w-1。符号位为1是负为0是正。补码的范围不对称,是因为:一半的数的整数一半是负数,而0是非负
数。最大的无符号数值刚好比补码的最大值的两倍大一点。
有符号数还有两种标准的表示方法:
反码:除了最高有效位的权是-(2w-1-1)而不是-2w-1,它和补码是一样的。
原码:最高有效位是符号位,用来确定剩下的位应该取负权还是正权。
4.有符号数和无符号数之间的转换:将函数U2Tw定义为U2Tw(x) = 4B2Tw(U2Bw(x))。这个函数的输入是一个0~2w - 1之间的数,结果得到一个-2w-1~2w-1-1之间的值,这里两个数有相同的位模式,除了参数是无符号的,而结果是以补码表示的。类似地,对于-2w-1~2w-1-1之间的值x,函数T2Uw定义为 T2Uw(x) = 4 B2Uw(T2Bw(x)),生成一个数的无符号表示和x的补码表示相同。
C语言转换的原则是底层的位保持不变。无到有:U2TW。有到无:T2UW
6 扩展一个数字的位表示在不同字长的整数之间转换,同时又保持数值不变。
零扩展:开头添0
7.截断数字:减少表示一个数字的位数。
2.3整数运算
1.无符号加法:无符号加法等价于计算和模上2w。可以通过简单的丢弃x + y的w + 1位表示的最高位,来计算这个数值。可以被视为模运算形式,等价于计算和模2^w。
溢出:完整的整数结果不能放到数据类型的字长限制中去
2.补码加法:负溢出得到的结果比整数和大16,正溢出得到的结果比整数小16.
3.补码的非
4.无符号乘法计算公式。
5.补码乘法:给定长度的两个为位向量,无符号乘积的位级与补码乘积的位级表示是相同的,这表明机器可以用一种乘法指令来进行有符号数和无符号数的乘法。
6.乘以常数:为了缩短计算时间,许多C语言编译器试着用移位,加法和减法运算的组合来代替乘以常数的乘法。
7.除以2的幂:除以2的幂可以通过逻辑或者算术右移来实现。
8.关于整数运算的最后的思考:计算机执行“整数”运算实际是一种模运算形式。表示数字的有限字长限制了可能的取值范围,结果可能溢出。补码提供了技能表示正数也能表示负数的灵活方法,同时使用了与执行无符号算数相同的位级实现。
2.4浮点数
1.二进制小数:辗转相除法,2的负幂。
2.IEEE浮点表示:
标准: V=(-1)^sM2^E。
符号:s决定数的正负。
尾数:M是二进制小数。
阶码:E的作用是对浮点数加权,权重是2 的E次幂。
情况1:规格化的值。当exp的为模不全为1或0。阶码字段被解释为以偏置形式表示有符号整数。
情况2:非规格化的值:当阶码域为全0时,所表示的数就是非规格化形式。在这种情况下,阶码值是E = 1 - Bias,而尾数的值是M = f,也就是小数字段的值,不包含隐含的开头的1
情况3:特殊值:阶码域全为1。小数域全为0,得到的值表示无穷。在表示未初始化的数据时也很有用。
3.数字示例
4.舍入:浮点运算只能近似的表示示数运算想要找到最接近x的值就是舍入,问题的关键在于在两个可能的值中间确定舍入方向。
默认方法找到做接近的匹配,其他三种用于计算上界和下界(向零舍入,向下舍入,向上舍入)。
向偶数舍入(默认):正数向上舍入,负数向下舍入。
5.浮点运算:IEEE标准指定了一个简单的规则,用来确定诸如加法和乘法这样的算术运算的结果。浮点加法不具有结合性但满足了单调性属性但只有有限的范围和精度。
6.C语言中的浮点数:float double



