20135202闫佳歆——信息安全系统设计基础第四周学习总结

第2章 信息的表示和处理

三种最重要的数字表示：

* 无符号
* 补码
* 浮点数

运算：

* 整数运算
* 浮点运算

对比：

整数运算只能编码相对较小的范围，但是是精确的；

浮点运算可以编码一个较大的范围，但是是近似的；浮点运算不可结合。

注意：溢出——运算位数的限制

第一节 信息存储

计算机最小的可寻址的存储器单位——字节

一个字节的值域：00H-FFH

一、十六进制表示法

1. C表示法

以0x或0X开头的数字常量为十六进制

2. 进制转换

常用进制：二进制（B），十进制（D），八进制（O或者Q），十六进制（H）

转换为二进制-十六进制相互转换，二进制的四位数字对应十六进制的一位数字。

同理，二进制与八进制的转化是三位对应一位。

但是通常情况下，进制转换都以二进制为桥梁进行转换。

※一种特殊情况

课本23页有这样一种情况，要表示的数字常量x=2的n次方时，n=i+4j，且0≤i≤3时，开头的十六进制数字为1（i=0）、2（i=1）、4（i=2）、8（i=3），后面跟随着j个十六进制的0。这里的j是代表着每四位二进制位对应的十六进制位，而i的范围是因为十六进制中每一位的范围是0-F，最多能容纳到8。这是一种方便快捷的计算方法。

二、字

字长决定虚拟地址空间的最大大小。

字长为w，虚拟地址的范围为1-(2^w-1)

w=32或64：也就是我们通常所说的电脑是32位还是64位。也可以理解为CPU一次处理数据的位数。

三、数据大小

在不同字长的计算机中，相同的数据类型所占用的字节数并不相同，32位和64位的区别参见教材26页表格。

gcc -m32 可以在64位机上生成32位的代码

四、寻址和字节顺序

1.小端法和大端法

• 小端法：最低有效字节在前面——“高对高，低对低”
• 大端法：最高有效字节在前面

注意：

有效位的高低的判断：

以0x01234567为例，每个字节为8bit所以2个十六进制位为1个字节，即划分为01,23,45,67；在最前面的为最高有效位，最后面的为最低有效位，所以最高有效位-01，最低有效位-67。

大端法：
最高有效位在最前，所以为01 23 45 67
小端法：
最低有效位在最前，所以为67 45 23 01

但是字节内部的顺序是不变的！以前在学汇编的时候经常犯这种错误！理解最高/低有效位的含义！

所以在书写小端法的字节序列时，最低有效位在左边，最高有效位在右边，与惯常书写方法相反。

2.强制类型转换

书28页代码

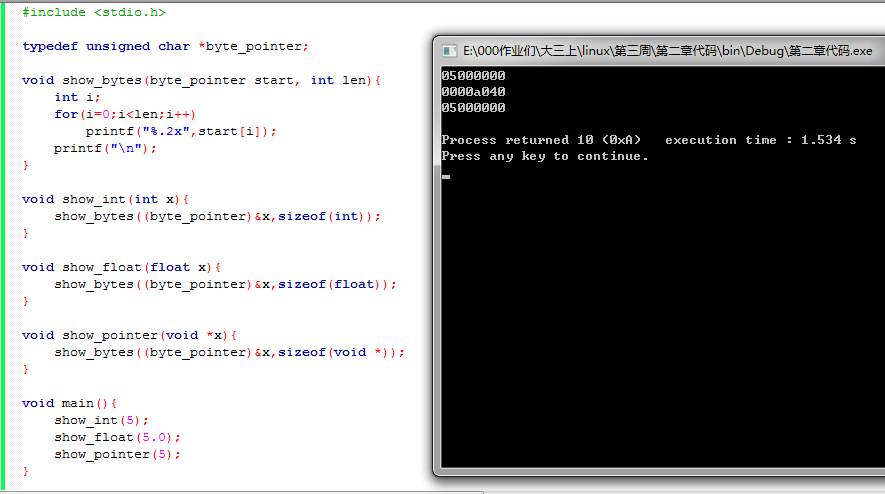
c语言知识回顾：

typedef：命名数据类型
sizeof（）：返回类型的字节数（好处？便于移植——32位和64位的区别）

五、表示字符串和表示代码

1.字符串

c语言中字符串被编码成为一个以null（值为0）字符结尾的字符数组。多使用ASCII字符码。

在使用ASCII字符码的任何系统上都能得到相同的结果，与字节顺序和字大小规则无关，所以文本数据比二进制数据具有更强的平台独立性。

2.代码

二进制代码在不同的操作系统上有不同的编码规则。所以二进制代码是不兼容的。

六、位运算

1.布尔代数

常用运算符号：

与： &
或： |
非： ~
异或：^

2.位向量

• 位向量：有固定长度为w、由0和1组成的串。

位向量的应用——表示有限集合。

3.位级运算

• 位运算：位向量按位进行逻辑运算，结果仍是位向量（区别于逻辑运算）

※常见用法：掩码——用来选择性的屏蔽信号

掩码是一个位模式，表示从一个字中选出的位的集合。

用位向量给集合编码，通过指定掩码来有选择的屏蔽或者不屏蔽一些信号，比如

某一位位置上为1时，表明信号i是有效的；0表示该信号被屏蔽。

这个掩码就表示有效信号的集合。

举一个掩码的例子：

0xFF，表示屏蔽除最低有效字节之外的所有字节。

所以任取一个数x=0x934ADFEC,x&0xFF=0x000000EC

• 位级表达式

位级表达式的计算，要将通过转化为二进制表示进行二进制运算再转换回原来的进制来进行。

~0：生成一个全1的掩码。

七、逻辑运算

逻辑运算符

与：&&
或：|| 
非：！ 

• 逻辑运算的计算方法：

所有非零参数都代表TRUE，0参数代表FALSE

• 逻辑运算的结果：

1-代表TRUE，或者，0-代表FALSE

逻辑运算和位运算的区别

1.只有当参数被限制为0或1时，逻辑运算才与按位运算有相同的行为。
2.如果对第一个参数求值就能确定表达式的结果，逻辑运算符就不会对后面的参数求值。

八、移位运算

1.c语言中的移位运算

（1）左移<<

x<<k 意味着将x向左移动k位，丢弃最高k位并且在右端补k个0。

（2）右移>>

右移分为逻辑右移和算术右移。（其实左移也区分，但是算术左移和逻辑左移没有什么区别）

• 逻辑右移：

  在左端补k个0，多用于无符号数移位运算

• 算术右移：

  在左端补k个最高有效位的值，多用于有符号数移位运算。

2.Java中的移位运算

Java中用>>表示算术右移，用>>>表示逻辑右移。左移同样。

3.优先级

移位运算的优先级比算术运算（比如+、-）要低

第二节 整数表示

一、整型数据类型

整型数据类型——表示有限范围的整数，每种类型都能用关键字来指定大小，还可以指定是非负数（unsigned）还是负数（默认）。这些不同大小的分配的字数会根据机器的字长和编译器有所不同。

关于取值范围

• 32位机器和64位机器对于同一数据类型的典型取值范围是有所不同的。
• 典型取值范围中，取值范围不对称——负数的范围比整数的范围大1。
• c语言标准定义的每种数据类型必须能够表示的最小的取值范围中，正数和负数的取值范围是对称的。

具体范围见书38页。

要用C99中的“long long”类型，编译是要用 gcc -std=c99

二、无符号数的编码

编码方法见书，已经在很多门课程中都学习过了。

需要注意的是无符号数的二进制表示的一个重要性质：

0-（2^w）-1中的每一个整数和长度为w的位向量是一一对应的。

三、补码编码——有符号数的编码

关于补码，一些可能没有注意过的知识：

• 我们都知道补码的最高位是表示符号位，解释为负权，“权重”为-2的（w-1）次方，即无符号表示中的权重的负数。符号位为1，表示值为负，符号位为0，表示值为非负（不是正，因为有0）
• 补码的映射关系同样是一一对应的
• 补码的范围：-2^(w-1)~2(w-1)-1，即|TMin|=|TMax|+1——因为非负数中0的存在。
• 无符号数编码（U）和补码（T）：UMax = 2 TMax + 1
• 大多数情况下用补码来表示有符号数，并且具有的是典型的取值范围。

有符号数的其他表示方法：

• 原码
• 反码

四、有符号数和无符号数的转换

1.强制类型转换

从位级角度考虑。

强制类型转换的结果保持位值不变，只是改变了解释这些位的方式。即：这些位上的值不变，但是由于最高有效位的权重发生变化，从而导致结果发生改变。

2.c语言中的有符号数和无符号数及其转换

转换原则：底层的位保持不变。

（1）有符号数→无符号数

• 非负数——保持不变
• 负数——转换成大正数

（2）无符号数→有符号数

以2的w-1次方为界限：

• 小于它——保持不变
• 大于它——转换为负数值

简而言之就是：

[0,2^{(w-1))这个范围内的数字，无符号和补码表示相同；范围之外的，需要加上或者减去2}w。

原因？最高位的权重在变化时是两倍的差值。

c语言中同时存在有符号数和无符号数？

会隐式的将有符号数强制类型转换为无符号数，并且假设这两个数都是非负的。

五、扩展

扩展——从一个较小的数据类型转换为较大的数据类型，同时保持数值不变。

1.零扩展

多用于无符号数转换为一个更大的数据类型。

只需在开头加上0即可。

2.符号扩展

多用于补码数字转换

最高有效位是什么，就添加什么。

注：无符号和有符号数字之间的转换，和数据的大小的转换，这之间的相对顺序能够影响到一个程序的行为。具体见联系2.23。

六、截断数字

不用额外的位来扩展数值，而是减少表示一个数字的位数。而这么做可能会改变它的值，这也是溢出的一种形式。

将一个w位的数截断为k位数字时，就会丢弃高w-k位。

对于无符号数来说，就相当于 mod 2的k次幂

对于有符号数来说，先按照无符号数截断，然后再转化为有符号数

具体的公式参见书52页。

七、关于书上的习题，需要知道的：

练习题2.25中，length=0时会出现存储器错误，这是因为定义了length为无符号数，根据之前的内容，这使得与之相关的运算和运算数都变成无符号的运算。0-1会出现错误不能计算，这是我的理解。

但是0-1出错的原因我想错了，不是不能进行计算，而是变成了无符号的模数运算后得到了最大值UMax，使得≤的条件恒成立，继而访问数组a的非法元素。

比较常用的修改方法是把length定义成int，但是另外一种方法也需要知道：把循环条件改为＜。

关于适用范围：

无符号数适用于没有任何数字意义的位的集合，比如地址；又或者实现模运算、多精度运算的时候，数字由字的数组表示的时候。

编程中多用有符号数。

第三节 整数运算

——实际上这是一种模运算。

一、无符号运算

无符号运算本质上就是模运算，mod 2的w次幂。

1.加法

涉及到的相关知识有：交换群（阿贝尔群），单位元，加法逆元等等。计算起来很简单。

2.乘法

两个w位的无符号数相乘，实际上是截取了低w位，但是等价于mod 2的w次幂。

总之就是模幂运算。

二、补码运算

1.加法

两个数的w位补码之和与无符号之和有完全相同的位级表示。

溢出

补码加法的溢出情况比无符号运算更为复杂，分为正溢出、正常、负溢出。正溢出就是超过正数的最大范围，负溢出就是超过负数的最大范围，具体的公式在书58页，正负溢出的范围和原因，直观一点的图在59页。

但是其实公式里给的本质仍然是模运算，模掉w位的补码最高有效位的权重2的w次幂。

2.非

（1）补码的非运算

对于范围在[-2^(w-1),2(w-1))中的x，补码的非运算有如下两种情况：

x=-2^{(w-1)时，为-2}(w-1)

x>-2^(w-1)时，为-x

（2）求位级补码非

• 对每一位求补，再对结果+1
• 设k为最右面的1的位置，将k左边的所有位取反。

3.乘法

c语言中的有符号乘法是通过将2w位的乘积截断为w位的方式实现的。也就是说，需要mod 2的w次幂。

所以：对于无符号和补码乘法来说，乘法运算的位级表示都是一样的。

三、乘以常数

在机器运算中，乘法总是很慢的，而加法和移位（左移）是相对较快的。所以在编译器中，会使用移位和加法运算组合的方式来代替乘以常数因子。这种方法对于无符号运算和补码运算都是适用的。

1.常数为2的k次幂的时候

直接左移k位即可。

2.常数不是2的整数次幂的时候

将常数C表示为2的几个整数次幂的和，结合移位运算和加法运算。

溢出？不影响结果。

四、除以2的幂

机器运算中，除法比乘法更慢。当被除数为2的整数次幂时，通过右移来解决。右移时需要区分无符号数和补码。

需要注意：整数除法总是舍入到零

1.无符号数——逻辑右移

无符号数除以2的k次幂，就等同于对其逻辑右移k位。

2.补码——算术右移

补码进行算术左移时，需要考虑补码数的正负，因为整数除法总是舍入到零，无符号数中没有负数不必担心，但补码中有正有负，正数向下舍入到零，负数应该向上舍入到零。所以这里涉及到在移位前偏置。
也就是说：

• x≥0时，除以2的k次幂等价于将x算术右移k位
• x＜0时，先将x加上(2^k)-1，再算术右移k位

与乘法不同，这种右移方法不能推广到任意常数C。

五、整数运算的总结

• 计算机执行的“整数运算”实际上是一种模运算。
• 无论运算数是以无符号形式还是补码形式表示，都有完全一样或者非常类似的位级行为。
• 在编写c语言程序时需要谨慎食用unsigned数据类型，很可能会造成漏洞。

第四节 浮点数

浮点表示对形如V=x X (2^y)的有理数进行编码，适用于：

非常大的数字
非常接近于0的数字
作为实数运算的近似值

一、二进制小数

小数的二进制表示法只能表示那些能够被写成x X (2^y)的数，其他的值只能近似的表示。

权重

以小数点为界：

左边第i位，权重为2的i次幂
右边第i位，权重为1/2的i次幂

二、IEEE浮点表示

IEEE浮点标准：

用V=(-1)^s X 2^E X M 来表示一个数：
符号：s决定这个数是正还是负。0的符号位特殊情况处理。
阶码：E对浮点数加权，权重是2的E次幂（可能为负数）
尾数：M是一个二进制小数，范围为1~2-ε或者0~1-ε（ε=1/2的n次幂）

编码规则：

单独符号位s编码符号s，占1位
k位的阶码字段exp编码阶码E
n位小数字段frac编码尾数M（同时需要依赖阶码字段的值是否为0）

两种精度

• 单精度（float），k=8位，n=23位，一共32位；
• 双精度（double），k=11位，n=52位，一共64位。

三种被编码情况

• 规格化的
• 非规格化的
• 特殊值

图见70页，更直观

1.规格化的值

即exp的位模式既不全0也不全1的时候，这是最一般最普遍的情况，因而是规格化的。

（1）阶码字段和阶码

这里是以偏置形式表示的有符号整数。

阶码E = e-Bias

Bias=[2^(k-1)-1]

（2）小数字段和尾数

二进制小数点在小数字段最高有效位的左边。

尾数M = 1+f（隐含的以1开头的表示）

2.非规格化的值

即阶码域全为0时的数。

（1）阶码

阶码E = 1-Bias

（2）尾数

尾数M = f（小数字段的值，不包含隐含的1）

（3）非规格化的功能：

a. 提供了一种表示数值0的方法。

b. 表示那些非常接近零的数。逐渐溢出

3.特殊值

特殊值是在阶码位全为1的时候出现的。分为两种情况：

（1）无穷

小数字段全为0

（2）NaN不是一个数

小数字段非0

一些运算的结果不能是实数或无穷的时候会返回这样的值。或者表示未初始化的数据。

关于以上的范例参见课本的71页，数字示例。IEEE的表示虽然在大一的计算机导论就已经学过，但是很久不用需要再捡起来。课本中的图是一个比较直观的展示，我们可以看到0的两种表示+0和-0，他们是特殊的非规格化数，还有密集遍布在0周围的那些数，他们是不均匀分布的，越靠近原点越稠密。

然后72页下面提到了最大非规格化数和最小规格化数的平滑转变，看到这里就可以理解对非规格化中对E的定义，它是因为非规格化中M的定义缺少前面的1所以改在E中补回来。

同时还可以看到一个属性，浮点数能够使用整数排序函数来进行排序

需要注意的题

课本72页整数值和单精度浮点值在位级表示上的关系：

相关的区域对应于整数的低位，在等于1的最高有效位之前停止（这个位就是隐含的开头的位1），和浮点表示的小数部分的高位是相匹配的。

这里还没有很看懂，需要多推导几遍。

三、舍入

首先我们要知道，浮点运算只能近似的表示实数运算。

舍入运算：找到和数值x最接近的匹配值x'，可以用期望的浮点形式表示出来。

IEEE浮点格式定义了四种不同的舍入方法：

1.向偶舍入（默认方法）

即：将数字向上或向下舍入，是的结果的最低有效数字为偶数。

能用于二进制小数。

2.向零舍入

即：把整数向下舍入，负数向上舍入。

3.向下舍入

正数和负数都向下舍入。

4.向上舍入

正数和负数都向上舍入。

默认的（即向偶舍入）方法可以得到最接近的匹配，其余三种可用于计算上界和下界。

我把向偶舍入看做平时管用的四舍五入的升级版，四舍六入，五求偶。

四、浮点运算

1.浮点加法

• 浮点加法是可交换的
• 浮点加法不具结合性
• 大多数值的浮点加法都有逆元，除了无穷和NaN。
• 浮点加法满足单调性

2.浮点乘法

• 浮点乘法是可交换的
• 浮点乘法不具有结核性
• 浮点乘法的单位元为1.0
• 浮点乘法在加法上不具备分配性
• 在一定条件下满足单调性：

五、c语言中的浮点数

int、float、double相互转换？

int → float 不会溢出但有可能舍入
int/float → double 结果保留精确数值
double → float 可能溢出为±∞，由于精确度较小也有可能被舍入
float/double → int 向零舍入，可能溢出。

总结

这一章给我的感觉是，首先课本把很多曾经学到的知识换了一种更专业也更难理解的方式说给我们听，许多乱七八糟的公式使得结果更正规完备的同时也给理解带来了难题，怎样从中摘取已经学习过的知识，转化成自己学习时候的理解并且予以更新，摘取出新知识学习，这样的一个行为给我的学习带来了很大的麻烦，我花了很长很长的时间来做这个工作。

然后关于这章的内容，很多东西都是看起来很熟悉，我们都曾学习过或者接触过，但是其实并不能清楚的知道其中的原理，就算学过的东西也会发现层次和深度都与原先不同。关于整数的表示，无符号和补码，知识的理解相对简单，但是如何迁移到c语言的编程中是一个大难题，我们很多时候已经习惯如何用哪个数据类型，但是没有思考过为什么其他的不可以。而IEEE浮点，之前在计算机导论中学习的时候只是略微知道了一些皮毛，现在看更是头大，应用到实践中就更吃力了。这都需要长久的温习和练习。