博客作业04--树

1.学习总结(2分)

1.1树结构思维导图

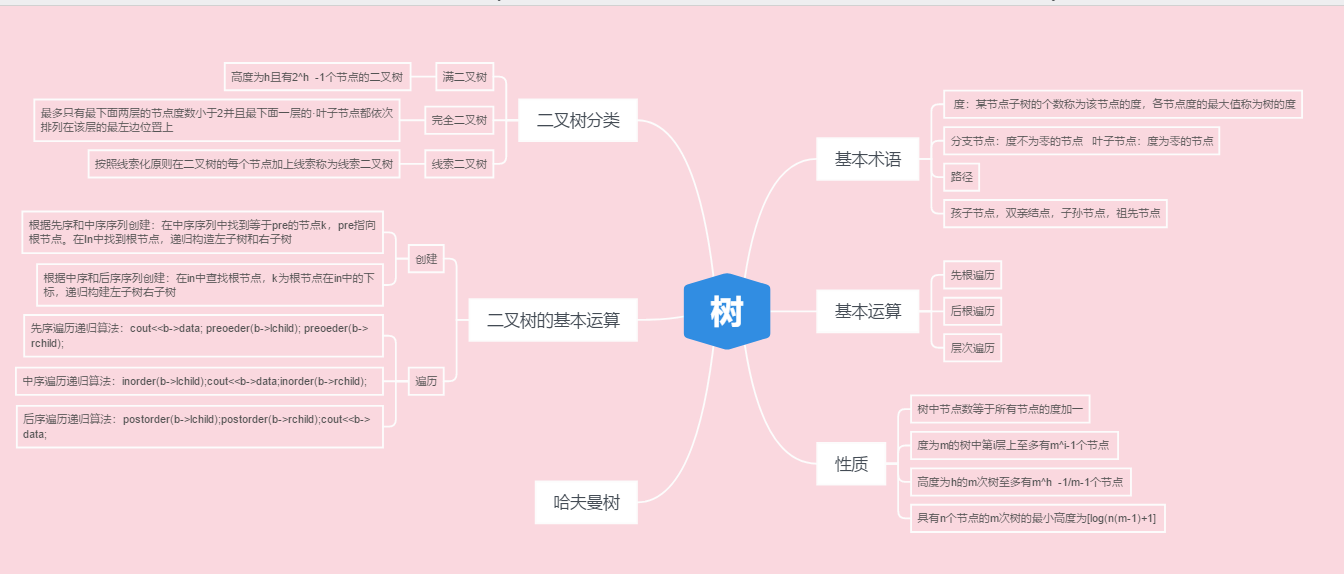
1.2 树结构学习体会

• 一开始觉得栈和队列就已经挺难的了，学了树之后，突然觉得树好像更难。哈夫曼树的编码到现在也不是很清楚要怎么编号。还有前缀转中缀的表达式转换也是有点迷糊。kmp就具体怎么转化的一开始学的时候好像感觉自己听懂了，后来期中考试的时候又忘记了，大概是没有真正理解导致的吧。还有kmp算法转化成代码，不是特别理解，只能照着书上模仿着写，自己写肯定写不出来。最后我发现在树的学习中，我又回到了以前的那种学习模式，敲代码照着书上写，不自己理解，所以一离开课本就完全不会了，后面的学习会首先改变这样的学习方法，不然以后不管是上机考试还是期末考试，恐怕都没办法好好考。在树的学习里，大概，就只是学会了前序遍历，中序遍历，和后序遍历吧，还有一些基本操作，稍微变形的话，对我来说是有难度的。

2.PTA实验作业（4分）

2.1 题目1： jmu-ds-表达式树

2.2 设计思路（伪代码或流程图）

     建表达式的二叉树
          stack<BTree>s1;
          stack<char>s2;
          while(str[i]){
         如果str[i]是数字{
          创建树节点并入栈}
         如果str[i]是字符{
             if (字符栈栈顶优先级小于str[i]){
          则进栈
             }
         else if(字符栈栈顶优先级大于str[i]){
         出栈并且从节点栈中出栈两个;
           构树并且放回节点栈中
           }}
           直接出栈
         
        计算表达式树
          double a,b
          a=EvaluateExTree(左子树)
          b=EvaluateExTree(右子树)
          switch(T->data){
               case'+': return a+b; break;
		case'-': return a-b; break;
		case'*': return a*b; break;
                ase'/': if(b==0){
			cout<<"divide 0 error!";}
               else  return a/b;

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明。

• 一开始没有理解表达式树的意思，直接建了一个普通的树，所以不管怎么试也不会对。
• 解决办法：在建立表达式树的过程中出现各种问题，比如元素无法入栈，后来这个问题是参考了舍友的代码，然后她又帮我调试了一些小问题才做出来的。
• 在计算表达式树的时候感觉自己的程序应该没有问题，但是编译就是过不了。
• 解决办法：我后来去网上找了一些有关于表达式树的代码，发现我是用a,b直接等于T->data,而且我不是用return 而是用了pop，所以编译老出错。后来发现问题之后，a,b等于
  EvaluateExTree(左子树) EvaluateExTree(右子树)就好了

2.1 题目2：还原二叉树

2.2 设计思路（伪代码或流程图）

       自定义一棵树BTree
       BTree t ； 
      定义两个字符数组pre[100],in[100]；分别存放先序序列和中序序列
      int i，n；n为树中结点总数
      int L,R分别表示左节点和右节点个数
      输入 n,pre,in;
      建二叉树{ 
           创建二叉树总节点t
              在中序序列中找到等于pre的节点
             pre 指向的为根节点
             确定根节点在in中的位置
             递归构造左子树和右子树
               }
      输出二叉树高度{
            L=heigth(T->lchild);
	    R=heigth(T->rchild)；
         返回L,R中大的那一个并且加一 }
         

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

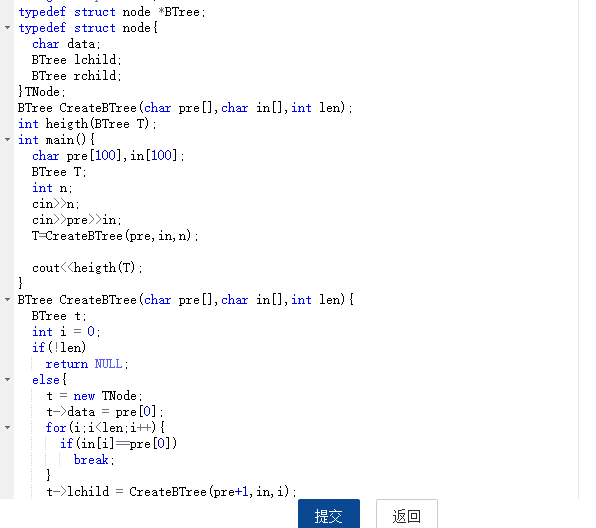
2.4 PTA提交列表说明。

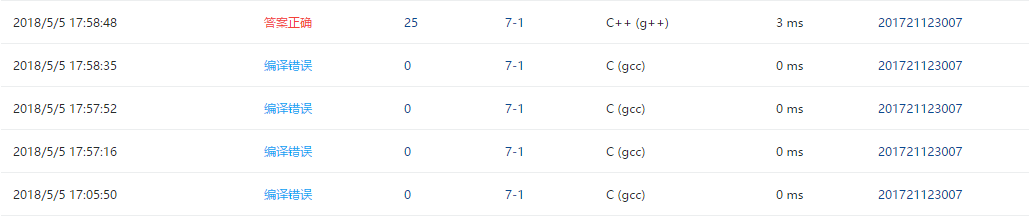
• 一开始建完树之后准备用先序，中序遍历二叉树后来发现没有输出的话先序和中序是一样的，所以感觉这样不太对劲，就不遍历了，直接计算高度。
• 我一开始照着课本的样子用指针节点来创建二叉树，后来不知道为什么编译一直过不去

错误代码

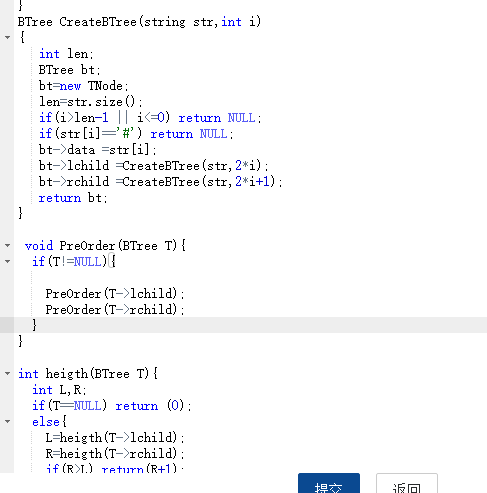
后来我也不知道要怎么改，所以干脆不用指针，直接用数组来存放，函数头里的变量也直接改成数组。

2.1 题目3：根据后序和中序遍历输出先序遍历

2.2 设计思路（伪代码或流程图）

        自定义一棵树Tree
       Tree T； 
      定义两个字符数组pre[100],in[100]；存放·后序和中序序列
      int num存放根节点在in中的下标
      创建二叉树{
          在In中查找根节点
          num存放根节点在in中的下标
          递归创建左子树右子树
          }
         递归法先序遍历二叉树
        输出先序遍历结果

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

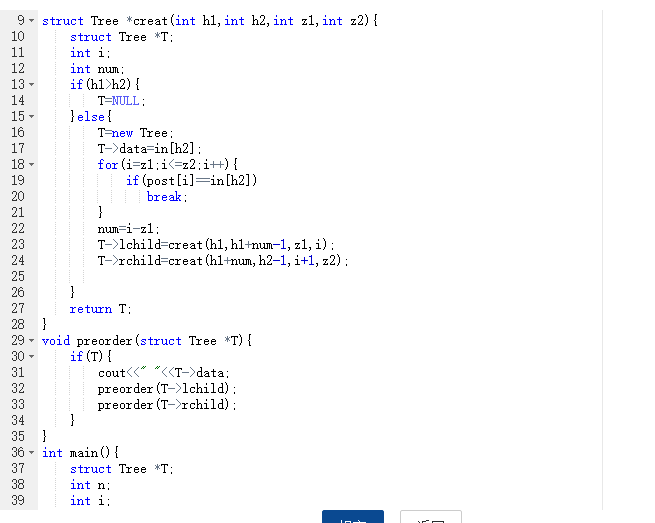
2.4 PTA提交列表说明。

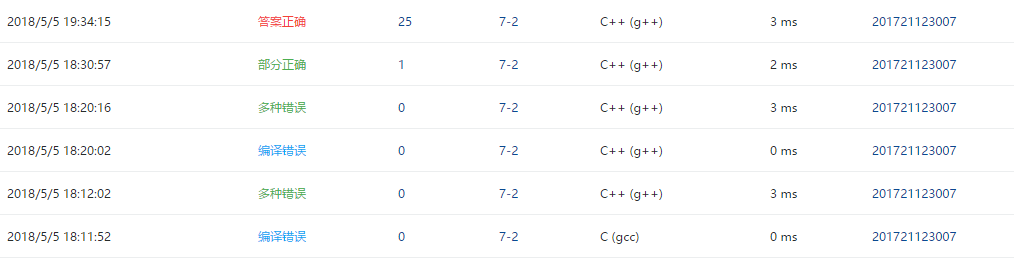
• 这一题跟7-1很像，但是后面在创建树的时候又错了，错误在于 T->right=creat(h1+num,h2-1,z1+num,z2); 中序的起始位置不正确，i的位置为根的位置，中序右子树的起始位置应该为根的右面第一个数据

3.截图本周题目集的PTA最后排名（3分）

3.1 PTA排名

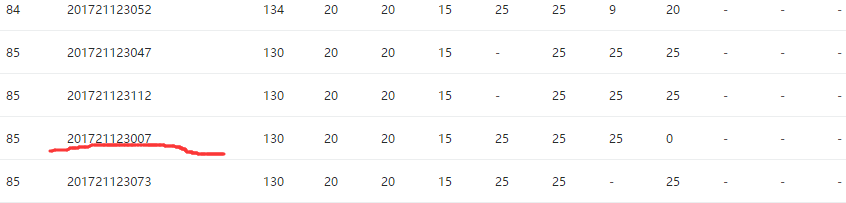
3.2 我的得分：

130

4. 阅读代码（必做，1分）

这段代码的功能是建立哈夫曼树

struct BTreeNode* CreateHuffman(ElemType a[], int n)  
{  
    int i, j;  
    struct BTreeNode **b, *q;  
    b = malloc(n*sizeof(struct BTreeNode));  
    for (i = 0; i < n; i++) //初始化b指针数组，使每个指针元素指向a数组中对应的元素结点  
    {  
        b[i] = malloc(sizeof(struct BTreeNode));  
        b[i]->data = a[i];  
        b[i]->left = b[i]->right = NULL;  
    }  
    for (i = 1; i < n; i++)//进行 n-1 次循环建立哈夫曼树  
    {  
        //k1表示森林中具有最小权值的树根结点的下标，k2为次最小的下标  
        int k1 = -1, k2;  
        for (j = 0; j < n; j++)//让k1初始指向森林中第一棵树，k2指向第二棵  
        {  
            if (b[j] != NULL && k1 == -1)  
            {  
                k1 = j;  
                continue;  
            }  
            if (b[j] != NULL)  
            {  
                k2 = j;  
                break;  
            }  
        }  
        for (j = k2; j < n; j++)//从当前森林中求出最小权值树和次最小  
        {  
            if (b[j] != NULL)  
            {  
                if (b[j]->data < b[k1]->data)  
                {  
                    k2 = k1;  
                    k1 = j;  
                }  
                else if (b[j]->data < b[k2]->data)  
                    k2 = j;  
            }  
        }  
        //由最小权值树和次最小权值树建立一棵新树，q指向树根结点  
        q = malloc(sizeof(struct BTreeNode));  
        q->data = b[k1]->data + b[k2]->data;  
        q->left = b[k1];  
        q->right = b[k2];  
  
        b[k1] = q;//将指向新树的指针赋给b指针数组中k1位置  
        b[k2] = NULL;//k2位置为空  
    }  
    free(b); //删除动态建立的数组b  
    return q; //返回整个哈夫曼树的树根指针  
}  

与课本构造哈夫曼树的方法略有不同，这个我比较容易理解一些，但是感觉好像课本代码才是精华，更为精简。

5. 代码Git提交记录截图