有向有权图的最短路径算法--Dijkstra算法

    

Dijkstra算法

1.定义概览

     Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，

在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

 

2.算法描述

 

       首先把起点到所有点的路径花费都设为无穷大（起点到起点的花费设为0），对于一个没有被标记过的且在没有标记过的点中从起点到这个点的花费最小（最开始一定是起点）点v,设起点到这个点的花费为v.dist， 如果点v到与它相邻的点w满足v.dist + <v,w>.weight < w.dist，其中<v,w>.weight表示从v到w的权值，那么就令w.dist = v.dist + <v,w>.weight ，并把节点v标记（不要标记w），重复以上步骤，直到所有点被标记，所有点的i.dist就是起点到这个点所要的最小花费。

 

3 代码实现

   按照上述思想，实现代码即可，图用邻接表表示。

 

   

#include <iostream>
using namespace std;
 
#define Inf 65535
#define NotAVerter -1

/////////////////////邻接表的相关定义//////////////////////
typedef struct EdgeNode *position;
typedef struct Led_table* Table; 


 struct EdgeNode     //边表结点  
{  
    int adjvex;    // 邻接点域,存储该顶点对应的下标  
    int weight;     // 对应边的权值 
    position next; // 链域,指向下一个邻接点
}; 

struct Led_table       // 邻接表结构  
{  
    int data;                //邻接表的大小
    position *firstedge;       //边表头指针，可以理解为数组
};  


//////////////////////////邻接表相关函数定义///////////////
Table Creat_Lable (int MaxElements)    //MaxElements参数为希望创建的节点数
{
	
	Table table1 = static_cast<Table> (malloc(sizeof(struct Led_table)));
	table1->data = MaxElements;
	if (table1 == NULL)
	{
	   cout << "out of space!!!";
	}

	table1->firstedge  = static_cast<position*>(malloc(sizeof(position)*(table1->data))); 
	if (table1->firstedge  == NULL)
	{
	   cout << "out of space!!!";
	}

	//给每个表头赋值，从0开始
	for (int i = 0; i <= table1->data - 1; ++i)
	{
	    table1->firstedge [i] = static_cast<position>(malloc(sizeof(EdgeNode)));   //申请一个节点
		if (table1->firstedge [i]  == NULL)
			{
			   cout << "out of space!!!";
			}
		table1->firstedge [i]->adjvex = 0;   //表头这个参数存储入度
		table1->firstedge [i]->weight = 0;   //此参数在此时没有意义
		table1->firstedge [i]->next = NULL;

	}
	return table1;

}


void Insert (Table table1, int v, int w, int weig)   //表示存在一条边为<v,w>,且权重为weig
{
    position p = static_cast<position>(malloc(sizeof(EdgeNode)));   //申请一个节点
	if(p == NULL)
	{
	   cout << "out of space!!!";
	}
	p->adjvex = w;
    p->weight = weig;
	p->next = table1->firstedge [v]->next;
	table1->firstedge [v]->next = p;
		
}


/////////////////////单源无权算法相关定义/////////////////////////
typedef struct unweight_path *unweight_node ;

 struct unweight_path     // 
{  
	bool know;
    int dist;    // 邻接点域,存储该顶点对应的下标  
    int path;     // 对应边的权值 
};

unweight_node unweight_init(Table table1, int start)     //节点初始化
{
	unweight_node Node  = static_cast<unweight_node>(malloc(sizeof(unweight_path)*(table1->data))); 
	if (Node  == NULL)
	{
	   cout << "out of space!!!";
	}
	for(int i = 0; i != table1->data; ++i)
	{
	    Node[i].know = false;
		Node[i].dist = Inf;
		Node[i].path = NotAVerter;
	}
	Node[start].dist = 0;
	return Node;
}

 ////////////////////////单源有权最短路径算法 Dijkstra /////////////////////////////

 void Dijkstra_Algorithm (Table table1,unweight_node Node)
 {
    int v;
	//用了两次for循环，时间复杂度较高
	for (int j = 0; j != table1->data; ++j)
	{
	    int zh = Inf;
		for (int i = 0; i != table1->data; ++i)    //找路径最小且没有标记过的点
		{
		   if(!Node[i].know && zh > Node[i].dist )  //如果这个点是未知的，且距离比较小
		   {
			  zh = Node[i].dist;
			  v = i;
		   }
	   
		}
		//此时v是距离最小的那个点
		Node[v].know = true;    //标记这个点
		position p = table1->firstedge [v]->next;
		while (p != NULL)   //与这个节点有连接的距离+1
		{
			if(!Node[p->adjvex].know && Node[v].dist + p->weight < Node[p->adjvex].dist )
			{
				Node[p->adjvex].dist = Node[v].dist + p->weight;
				Node[p->adjvex].path = v;
			}
			p = p->next;
		}

	}
	

 }

 /////////////////////打印实际的有权最短路径///////////////////////////////
 //采用递归算法，从后往前推
 void PrintPath (int v, unweight_node Node)    
 {
    if(Node[v].path != NotAVerter)
	{
	  PrintPath (Node[v].path ,Node);
	  cout << " -> ";

	}
	cout  << "v" << v;
 }

int main ()
{
  Table table_1 = Creat_Lable (7);    //创建一个大小为7的邻接表

  //根据图来为邻接表插入数据
  
  Insert (table_1, 0, 1, 2);Insert (table_1, 0, 2, 4);Insert (table_1, 0, 3, 1);
  Insert (table_1, 1, 3, 3);Insert (table_1, 1, 4, 10);
  Insert (table_1, 2, 5, 5);
  Insert (table_1, 3, 2, 2);Insert (table_1, 3, 5, 8);Insert (table_1, 3, 6, 4);
  Insert (table_1, 4, 3, 2);Insert (table_1, 4, 6, 6);
  Insert (table_1, 6, 5, 1);
  
  unweight_node Node_1 = unweight_init(table_1, 0);   //初始化节点
 
 Dijkstra_Algorithm (table_1, Node_1);
   for (int i = 0; i != table_1->data; ++i)
  {
     cout << Node_1[i].dist << '\t';
  }
  cout << endl;
  PrintPath (6, Node_1);
   while(1);
   return 0;
}

　　

　　对于下图来说

 

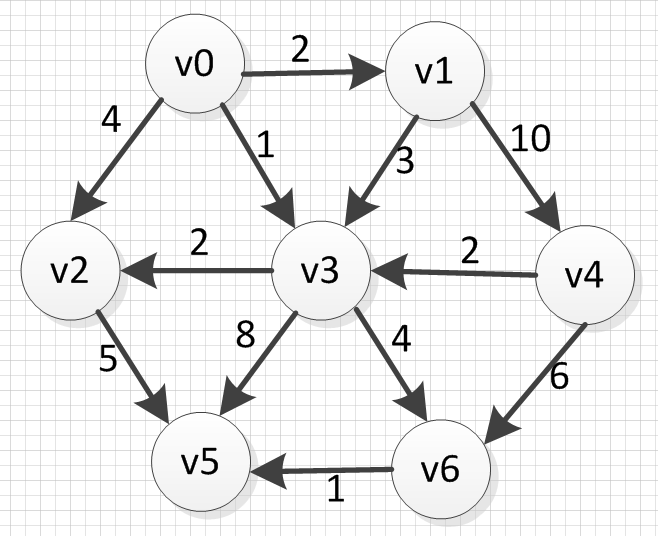
  以v0为起点，到各点的最短路径为：

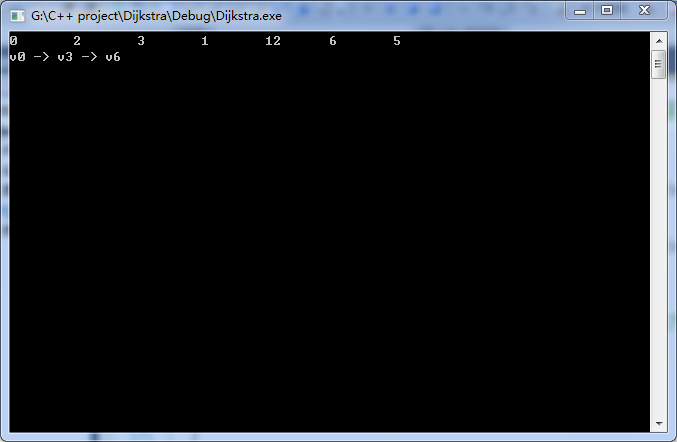
下面的v0->v3->v6表示v0到v6的最短路径经过的点。

 Dijkstra算法是典型的贪婪算法，并不能保证100%的正确率。

  也可参考 http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html  这篇博客的思想，本质上差不多。

  夜深了.....